数据结构——中缀转后缀表达式
Posted wkfvawl
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构——中缀转后缀表达式相关的知识,希望对你有一定的参考价值。
一、手工方式
如果只是用于解题的话,这种方法是最快最准确的。但是它不适用于计算机。下面以a+b*c+(d*e+f)*g为例子讲以下人应该怎么把中缀表达式转换成后缀表达式。
-
按先加减后乘除的原则给表达式加括号
结果:
((a+(b*c))+(((d*e)+f)*g)) -
由内到外把每个括号里的表达式换成后缀
最终结果:
abc*+de*f+g*+
这样就得到了中缀表达式转后缀表达式的最终结果。此法应付考试有神效。
二、栈的方式
计算机毕竟没有人的思路,需要借助栈来实现从中缀表达式到后缀表达式的转换。
这里明确一下使用栈转换的算法思想
从左到右开始扫描中缀表达式
遇到数字, 直接输出
遇到运算符
a.若为“(” 直接入栈
b.若为“)” 将符号栈中的元素依次出栈并输出, 直到 “(“, “(“只出栈, 不输出
c.若为其他符号, 将符号栈中的元素依次出栈并输出, 直到遇到比当前符号优先级更低的符号或者”(“。 将当前符号入栈。
扫描完后, 将栈中剩余符号依次输出
下面以a+b*c+(d*e+f)*g为例子来讲讲计算机的转换过程。下面在描述栈的情况是直接用文字描述了,由左到右为栈底到栈顶。空表示栈空
-
由左向右遍历表达式,首先遇到a,直接将其输出。
此时输出为:
a栈的情况为:空
-
继续遍历,遇到+,将其放入栈中。
此时输出为:
a栈的情况为:+
-
继续遍历,遇到b,直接将其输出。
此时输出为:
ab栈的情况为:+
-
继续遍历,遇到*,因为*的优先级大于栈顶的+,所以将*放入栈内。
此时输出为:
ab栈的情况为:+*
-
继续遍历,遇到c,直接将其输出。
此时输出为:
abc栈的情况为:+*
-
继续遍历,遇到+,因为+的优先级低于栈顶的*,故将*弹出;然后新的栈顶元素的+与这个+优先级相同,故也要弹出现在栈顶的+;然后栈空了,将现在这个+放入栈中。
此时输出为:
abc*+栈的情况为:+
-
继续遍历,遇到(,直接将其放入栈中,不遇到)不会将(弹出。
此时输出为:
abc*+栈的情况为:+(
-
继续遍历,遇到d,直接将其输出。
此时输出为:
abc*+d栈的情况为:+(
-
继续遍历,遇到*,因为栈顶为(,不遇到)不将(弹出,故直接将*放入栈中。
此时输出为:
abc*+d栈的情况为:+(*
-
继续遍历,遇到e,直接将其输出。
此时输出为:
abc*+de栈的情况为:+(*
-
继续遍历,遇到+,因为+比栈顶*的优先级低,故将*弹出;新的栈顶元素为(,不遇到)不弹出(,故将+放入栈中。
此时输出为:
abc*+de*栈的情况为:+(+
-
继续遍历,遇到f,直接将其输出。
此时输出为:
abc*+de*f栈的情况为:+(+
-
继续遍历,遇到),直接将栈中元素依次弹出并输出直到遇到(为止,注意:(弹出但不输出。
此时输出为:
abc*+de*f+栈的情况为:+
-
继续遍历,遇到*,因为*的优先级大于栈顶元素+的优先级,故直接将*入栈。
此时输出为:
abc*+de*f+栈的情况为:+*
-
继续遍历,遇到g,直接将其输出。
此时输出为:
abc*+de*f+g栈的情况为:+*
-
继续遍历,为空,遍历结束。将栈内元素依次弹出。
此时输出为:
abc*+de*f+g*+栈的情况为:空
至此,中缀表达式转后缀已经全部完成,结果为abc*+de*f+g*+。
三、代码实现
借助C++的stack实现
//中缀表达式转后缀 #include<iostream> #include<string> #include<stack> using namespace std; int prio(char op) //给运算符优先级排序 { int priority; if (op == ‘*‘ || op == ‘/‘) priority = 2; if (op == ‘+‘ || op == ‘-‘) priority = 1; if (op == ‘(‘) priority = 0; return priority; } bool Trans(string &str,string &str1) //引用传递 { stack<char> s; //定义一个char类型的栈s int i; for (i = 0; i<str.size(); i++) { if (str[i] >= ‘0‘ && str[i] <= ‘9‘||str[i] >= ‘a‘ && str[i] <= ‘z‘) //如果是数字,直接入栈 { str1+=str[i]; } else //否则不是数字 { if (s.empty()) //栈空则入站 s.push(str[i]); else if (str[i] == ‘(‘) //左括号入栈 s.push(str[i]); else if (str[i] == ‘)‘) //如果是右括号,只要栈顶不是左括号,就弹出并输出 { while (s.top() != ‘(‘) { str1+= s.top(); s.pop(); } s.pop(); //弹出左括号,但不输出 } else { while (prio(str[i]) <= prio(s.top())) //栈顶优先级大于等于当前运算符,则输出 { str1+= s.top(); s.pop(); if (s.empty()) //栈为空,停止 break; } s.push(str[i]); //把当前运算符入栈 } } } while (!s.empty()) //最后,如果栈不空,则弹出所有元素并输出 { str1+= s.top(); s.pop(); } return true; } int main() //主程序 { string infix; string postfix; cout << "请输入中缀表达式:" << infix << endl; cin >> infix; Trans(infix,postfix); cout << "后缀表达式为:" << postfix << endl; return 1; }

测试通过!
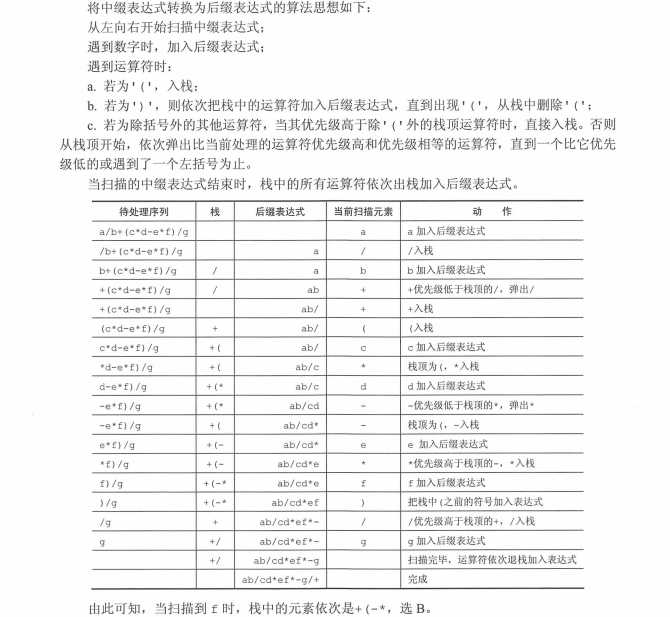
四、考研例题



以上是关于数据结构——中缀转后缀表达式的主要内容,如果未能解决你的问题,请参考以下文章