动态规划类问题

Posted 2020-12-14 arthas8086

动态规划类问题主要分为两大类：

1.求最优解（典型的背包问题）

2.计数（统计方案）

以上两类都存在递推性质。

第一类的递推称为最优子结构 -- 当前问题的最优解取决于子问题的最优解。

当前问题的方案数取决于子问题的方案数时，也可以用动态规划解决。

 

第二类例子：

机器人走方格（leetcode63.不同路径II）

机器人在一个m * n网格左上角走到右下角的路径数（只能向右或向下）。

 

 

网格数组为vector<vector<int>> obstacleGrid ,中间存在障碍物，当数组值为1时障碍物，为0无障碍物。

 

求方案数 ----> 动态规划  ---->状态转移方程

 走到最后一格的路径数肯定取决于一步走到最后一格的路径数，这样就能写出状态转移方程。

 

 

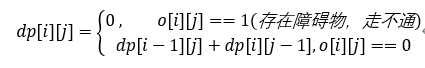
有了状态转移方程就可以写代码了。

 1 class Solution {
 2 public:
 3     int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
 4         int n = obstacleGrid.size(), m = obstacleGrid[0].size();
 5         vector<vector<int>> dp(n,vector<int>(m));
 6         dp[0][0] = 1;
 7         for(int i = 0; i < n; i++)
 8             for(int j = 0; j < m; j++)
 9             {
10                 if(obstacleGrid[i][j] == 1) dp[i][j] = 0;
11                 else 
12                 {
13                     if(i == 0 && j >= 1) dp[i][j] = dp[i][j - 1];
14                     else if(j == 0 && i >= 1) dp[i][j] = dp[i - 1][j];
15                     else if(i >= 1 && j >= 1)dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
16                 }
17             }
18         return dp[n - 1][m - 1];
19     }
20 };

主要需要注意的就是边界值的初始化。

 

在这里说一下滚动数组思想

滚动数组是动态规划类问题中一种编程思想。简单来说就是让数组滚动起来，

每次都使用固定的几个存储空间来达到压缩的目的，起到节省空间的效果。

往往dp 问题都是自底向上的扩展过程，前面的解往往可以舍去。

比如上面这道题用滚动数组思想的话，写法入下：

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int n = obstacleGrid.size(), m = obstacleGrid.at(0).size();
        vector <int> f(m);
        f[0] = (obstacleGrid[0][0] == 0);
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (obstacleGrid[i][j] == 1) {
                    f[j] = 0;
                    continue;
                }
                if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
                    f[j] += f[j - 1];
                }
            }
        }

        return f.back();
    }
};

 

这里解释一下为什么能这样优化。

假设我们的矩阵是

 

按照滚动数组遍历到第二行时，第一行的值只有在第二行的时候才会用到，第三行开始用不到了，因而可以使用完就舍弃。