13-自平衡二分搜索树 AVLTree
Posted sout-ch233
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了13-自平衡二分搜索树 AVLTree相关的知识,希望对你有一定的参考价值。
1、简介
? 在计算机科学中,AVL树是最早被发明的自平衡二叉查找树。在AVL树中,任一结点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O(log n)。增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡。AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。
? 结点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子1、0或 -1的结点被认为是平衡的。带有平衡因子 -2或2的结点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个结点中,或从可能存储在结点中的子树高度计算出来。
? AVL树的特点简单总结为以下:
- 又称为平衡二分搜索树
- 任一结点的左、右子树也均为AVL树
- 任一结点的平衡因子绝对值不超过1
- AVL树的高度和结点数量之间的关系也是O(logn)的
非AVL树实例:

AVL树实例:
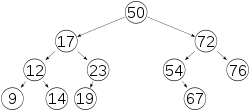
2、AVL的实现
2.1、实现原理
? 由AVL树的概念可知,要想实现一棵AVL树,我们只需要让二分搜索树实现平衡即可。所以:
- 记录每个结点的高度:非叶子结点的高度等于左右子树中最大的高度 + 1,叶子结点的高度为1,空结点的高度为0
- 计算平衡因子:左右子树的高度差,左 - 右(或右 - 左)。
- 通过"AVL旋转"维护平衡
- 维护平衡发生在添加新结点后
- 加入新结点后,沿着结点向上维护平衡性
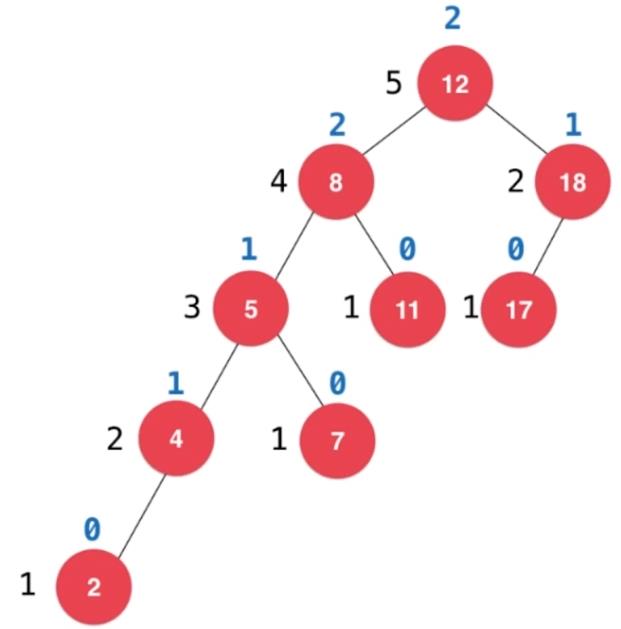
2.2、旋转的原理分析
向一棵AVL树中添加新的结点后,可能会破坏其原有的平衡性,因此需要维护平衡性。
树的不平衡形状有四种,相应的有四种"AVL旋转"。
2.2.1、LL,右旋转
新插入的元素在不平衡的结点的左侧的左侧,LL。(从 x 的角度看这是顺时针旋转,因此称为右旋转。)
判断条件:当前结点的平衡因子大于 1 并且其左孩子的平衡因子大于等于 0 。
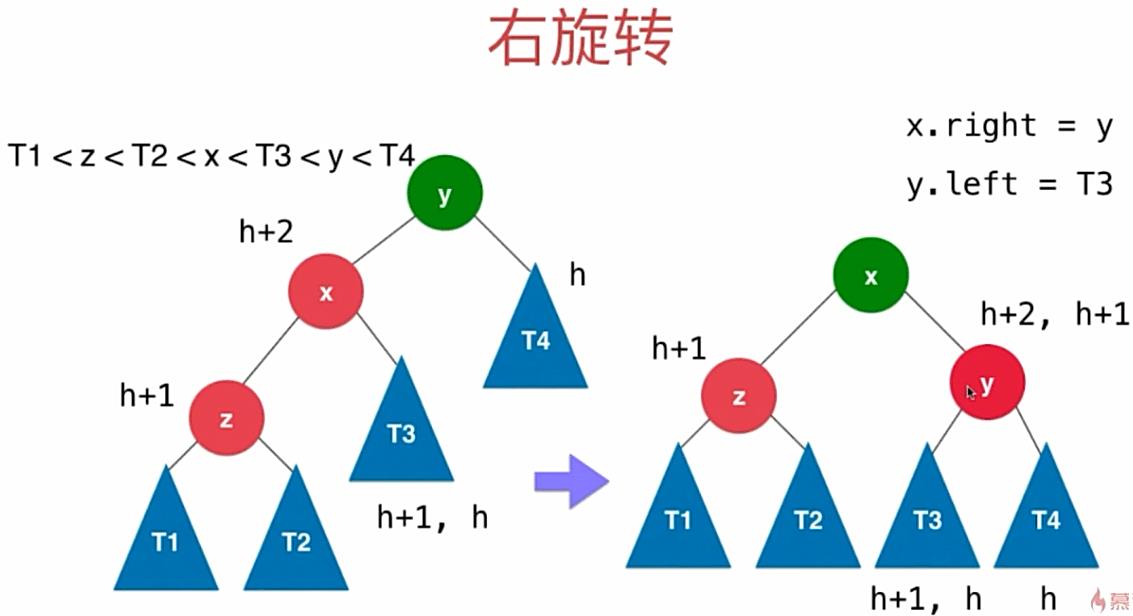
// 对节点y进行向右旋转操作,返回旋转后新的根节点x
// y x
// / / // x T4 向右旋转 (y) z y
// / - - - - - - - -> / / // z T3 T1 T2 T3 T4
// / // T1 T2
private Node rightRotate(Node y){
Node x = y.left;
Node T3 = x.right;
// 向右旋转过程
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
2.2.2、RR,左旋转
新插入的元素在不平衡的结点的右侧的右侧,RR
判断条件:当前结点的平衡因子小于 -1 并且其右孩子的平衡因子小于等于 0 。
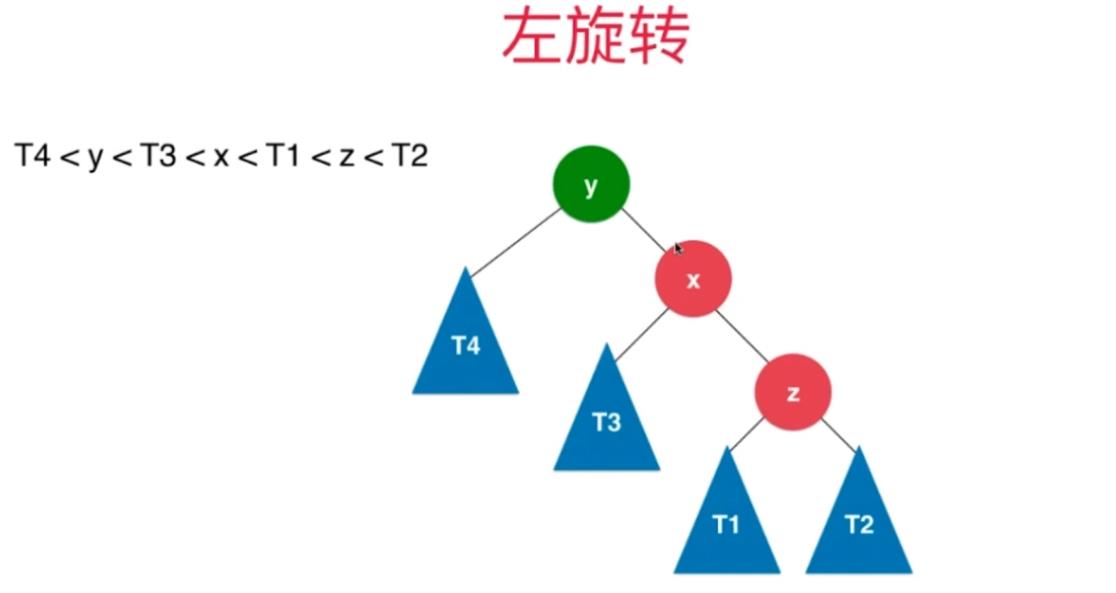
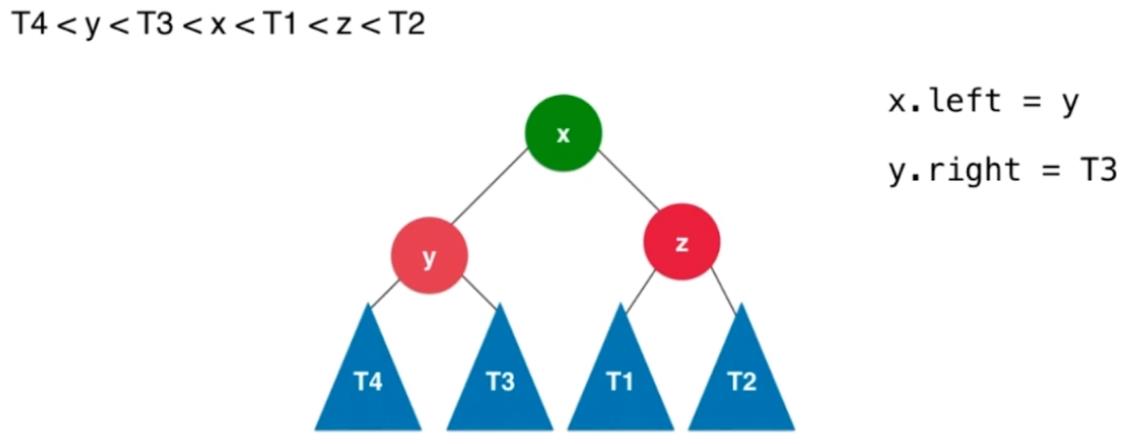
// 对节点y进行向左旋转操作,返回旋转后新的根节点x
// y x
// / / // T1 x 向左旋转 (y) y z
// / - - - - - - - -> / / // T2 z T1 T2 T3 T4
// / // T3 T4
private Node leftRotate(Node y) {
Node x = y.right;
Node T2 = x.left;
// 向左旋转过程
x.left = y;
y.right = T2;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
2.2.3、LR
新插入的元素在不平衡的结点的左侧的右侧,LR。
实例:
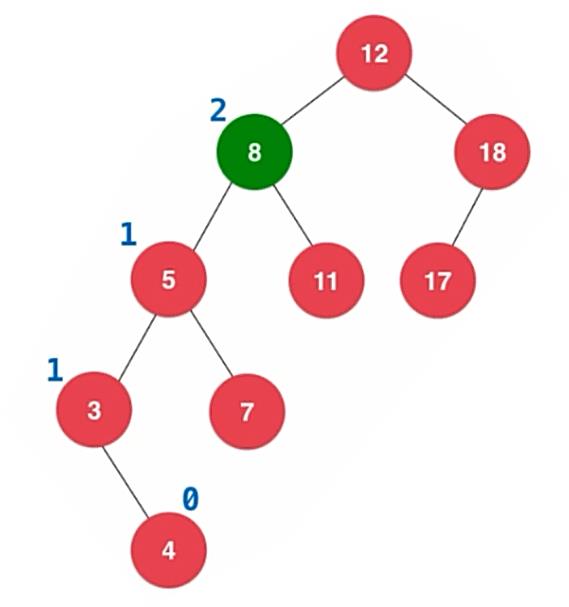
一般实例:
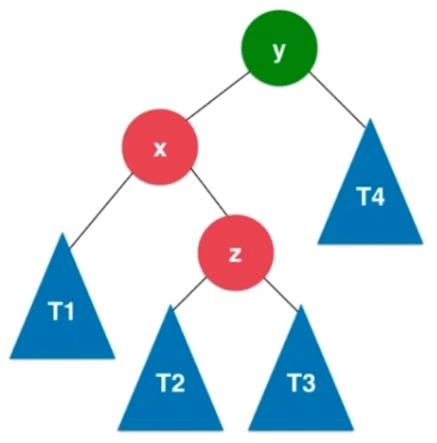
判断条件:当前结点的平衡因子大于 1 并且其左孩子的平衡因子小于 0 。
处理方式:先对x进行左旋转,再对y进行右旋转
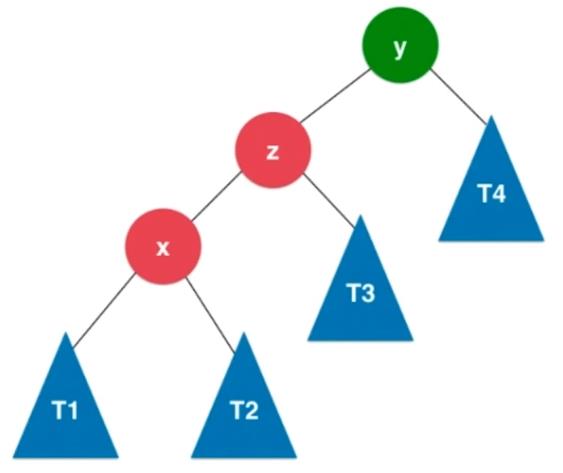
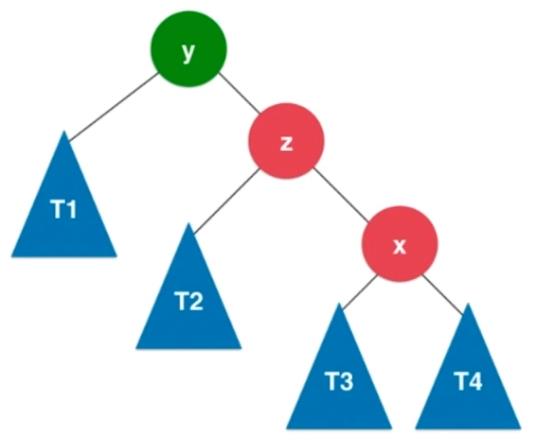
2.2.4、RL
插入的元素在不平衡的结点的右侧的左侧,RL。
一般实例:
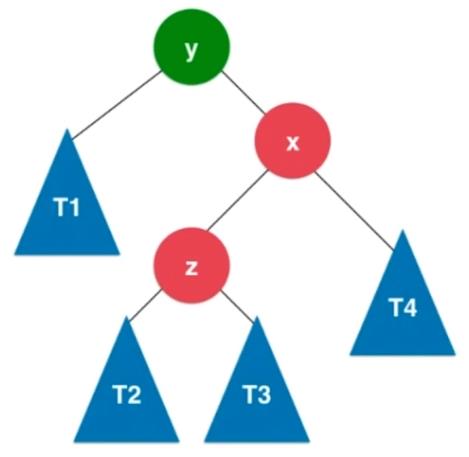
判断条件:当前结点的平衡因子小于 -1 并且其右孩子的平衡因子大于 0 。
处理方式:先对x进行右旋转,再对y进行左旋转
2.3、删除结点
AVL树在删除结点后,不仅要维护二分搜索树的的性质,同时也要维护平衡性。
// 从二分搜索树中删除键为key的节点
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
Node retNode = null;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
retNode = node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
retNode = node;
}
else{ // key.compareTo(node.key) == 0
if(node.left == null){ // 待删除节点左子树为空的情况
Node rightNode = node.right;
node.right = null;
size --;
retNode = rightNode;
}else if(node.right == null){ // 待删除节点右子树为空的情况
Node leftNode = node.left;
node.left = null;
size --;
retNode = leftNode;
}else {
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = remove(node.right, successor.key);
successor.left = node.left;
node.left = node.right = null;
retNode = successor;
}
}
if(retNode == null){
return null;
}
retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
int balanceFactor = getBalanceFactor(retNode);
if(balanceFactor > 1){
System.out.println("不平衡因子" + balanceFactor);
}
if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
return rightRotate(retNode);
}
if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
return leftRotate(retNode);
}
if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
retNode.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
return retNode;
}
2.4、代码
这里实现的AVL树,是基于之前实现的BSTMap改进而来的。(BSTMap与BSTTree并无本质区别)
import utils.FileOperation;
import java.util.ArrayList;
public class AVLTree<K extends Comparable<K>, V> {
private class Node{
public K key;
public V value;
public Node left, right;
// 节点高度
public int height;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
height = 1;
}
}
private Node root;
private int size;
public AVLTree(){
root = null;
size = 0;
}
// 获得节点的高度
private int getHeight(Node node){
if(node == null){
return 0;
}
return node.height;
}
// 获得节点的平衡因子
private int getBalanceFactor(Node node){
if(node == null){
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 判断当前树是否为二分搜索树,中序遍历key并输出到数组中,然后遍历数组判断BST性质
public boolean isBST(){
ArrayList<K> keys = new ArrayList<>();
inOrder(root, keys);
for(int i = 1; i<keys.size(); i++){
if(keys.get(i-1).compareTo(keys.get(i)) > 0){
return false;
}
}
return true;
}
// 中序遍历,参数1:遍历的树的根节点,参数2:一个数组
private void inOrder(Node node, ArrayList<K> keys){
if(node == null){
return;
}
inOrder(node.left, keys);
keys.add(node.key);
inOrder(node.right, keys);
}
// 判断当前树是否为平衡二叉树
public boolean isBalance(){
return isBalance(root);
}
private boolean isBalance(Node node){
if(node == null){
return true;
}
int balanceFactor = getBalanceFactor(node);
if(Math.abs(balanceFactor) > 1)
return false;
return isBalance(node.left) && isBalance(node.right);
}
// 向二分搜索树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
}
// 向以node为根的二分搜索树中插入元素(key, value),递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
// 更新height
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
int balanceFactor = getBalanceFactor(node);
// if(balanceFactor > 1){
// System.out.println("不平衡因子:" + balanceFactor);
// }
// LL
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
return rightRotate(node);
}
// RR
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
return leftRotate(node);
}
// LR
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// 对节点y进行向右旋转操作,返回旋转后新的根节点x
// y x
// / / // x T4 向右旋转 (y) z y
// / - - - - - - - -> / / // z T3 T1 T2 T3 T4
// / // T1 T2
private Node rightRotate(Node y){
Node x = y.left;
Node T3 = x.right;
// 向右旋转过程
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
// 对节点y进行向左旋转操作,返回旋转后新的根节点x
// y x
// / / // T1 x 向左旋转 (y) y z
// / - - - - - - - -> / / // T2 z T1 T2 T3 T4
// / // T3 T4
private Node leftRotate(Node y) {
Node x = y.right;
Node T2 = x.left;
// 向左旋转过程
x.left = y;
y.right = T2;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn‘e exist!");
node.value = newValue;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// 从二分搜索树中删除键为key的节点
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
Node retNode = null;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
retNode = node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
retNode = node;
}
else{ // key.compareTo(node.key) == 0
if(node.left == null){ // 待删除节点左子树为空的情况
Node rightNode = node.right;
node.right = null;
size --;
retNode = rightNode;
}else if(node.right == null){ // 待删除节点右子树为空的情况
Node leftNode = node.left;
node.left = null;
size --;
retNode = leftNode;
}else {
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = remove(node.right, successor.key);
successor.left = node.left;
node.left = node.right = null;
retNode = successor;
}
}
if(retNode == null){
return null;
}
retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
int balanceFactor = getBalanceFactor(retNode);
// if(balanceFactor > 1){
// System.out.println("不平衡因子" + balanceFactor);
// }
if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
return rightRotate(retNode);
}
if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
return leftRotate(retNode);
}
if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
retNode.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
return retNode;
}
}
3、测试
3.1、测试1
依然进行统计《计傲慢与偏见》文本的词汇量。FileOperation和傲慢与偏见的下载地址,提取码:g2b5
public static void main(String[] args){
System.out.println("Pride and Prejudice");
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
AVLTree<String, Integer> map = new AVLTree<String, Integer>();
for (String word : words) {
if (map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of PRIDE: " + map.get("pride"));
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
System.out.println("是不是一棵BST树" + map.isBST());
System.out.println("是不是一棵平衡二叉树:"+map.isBalance());
System.out.println("是不是一棵AVL树" + map.isBalance());
}
System.out.println();
}
3.2、测试2
public static void main(String[] args) {
System.out.println("Pride and Prejudice");
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
// 添加本行代码,所有单词将进行排序,则二分搜索树将直接退化为一个链表
// Collections.sort(words);
// Test BST
long startTime = System.currentTimeMillis();
BSTMap<String, Integer> bst = new BSTMap<>();
for (String word : words) {
if (bst.contains(word))
bst.set(word, bst.get(word) + 1);
else
bst.add(word, 1);
}
for(String word: words)
bst.contains(word);
long endTime = System.currentTimeMillis();
double time = endTime - startTime);
System.out.println("BST: " + time + " ms");
// Test AVL Tree
startTime = System.currentTimeMillis();
AVLTree<String, Integer> avl = new AVLTree<>();
for (String word : words) {
if (avl.contains(word))
avl.set(word, avl.get(word) + 1);
else
avl.add(word, 1);
}
for(String word: words)
avl.contains(word);
endTime = System.currentTimeMillis();
time = endTime - startTime;
System.out.println("AVL: " + time + " ms");
}
System.out.println();
}
4、基于AVL树的高层数据结构
4.1、基于AVL树的Map
package AVLTree;
public class AVLMap<K extends Comparable<K>, V> implements Map<K, V> {
private AVLTree<K,V> avl;
public AVLMap() {
this.avl = new AVLTree<K, V>();
}
@Override
public void add(K key, V value) {
avl.add(key,value);
}
@Override
public V remove(K key) {
return avl.remove(key);
}
@Override
public boolean ifContains(K key) {
return avl.contains(key);
}
@Override
public V get(K key) {
return avl.get(key);
}
@Override
public void set(K key, V newValue) {
avl.set(key,newValue);
}
@Override
public int getSize() {
return avl.getSize();
}
@Override
public boolean isEmpty() {
return avl.isEmpty();
}
}
4.2、基于AVL树的Set
package AVLTree;
public class AVLSet<E extends Comparable<E>> implements Set<E>{
private AVLTree<E, Object> avl;
public AVLSet() {
this.avl = new AVLTree<E, Object>();
}
@Override
public void add(E e) {
avl.add(e, null);
}
@Override
public void remove(E e) {
avl.remove(e);
}
@Override
public boolean ifContains(E e) {
return avl.contains(e);
}
@Override
public int getSize() {
return avl.getSize();
}
@Override
public boolean isEmpty() {
return avl.isEmpty();
}
}
以上是关于13-自平衡二分搜索树 AVLTree的主要内容,如果未能解决你的问题,请参考以下文章