支持向量机-分类器之王

Posted 2020-12-14 liyuewdsgame

1. 支持向量机（Support Vector Machine, SVM）：

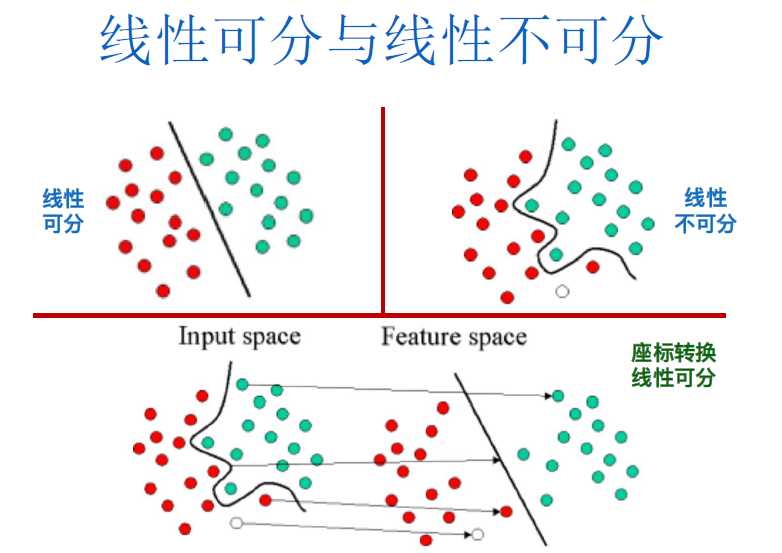
　　一种知名的二元线性/非线性分类方法，由俄罗斯的统计学家Vapnik等人所提出。它使用一个非线性转换(Nonlinear Transformation)将原始数据映像(Mapping)至较高维度的特征空间 (Feature Space) 中， 然后在高维度特征空间中，它找出一个最佳的线性分割超平面(Linear Optimal Separating Hyperplane) 来将这两个类别的数据分割开来。

 

 

 

 2.决策边界和支持向量

• （1）此分割超平面也可称为决策边界(Decision Boundary)， 藉由挑选适当的非线性转换，以及将数据映像至足够高维度的特征空间，这两个类别的数据在高维度特征空间中通常能被一个超平面分隔开来
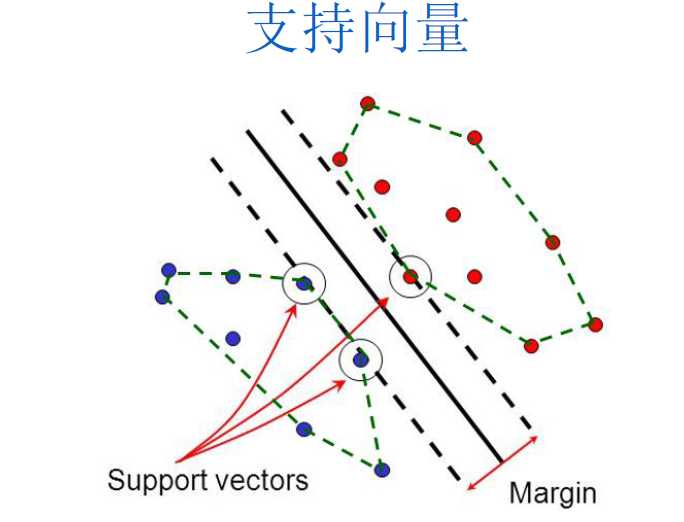
• （2）SVM利用支持向量(Support Vector)作为建构分割超平面的重要数据。
• （3）最佳的超平面是指：边界(Margin)最大化的超平面。
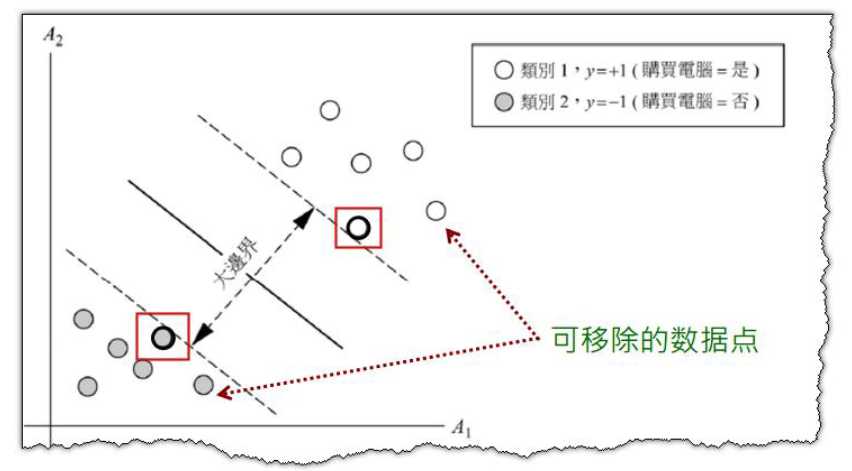
• （4）支持向量（Support Vector）定义：落在最佳超平面边界的边缘上的数据。支持向量是最重要且最关键的训练数据，因为它们是最难被分类正确的，如果它们能正确分类，其他数据都可以正确分类了。换句话说，如果我们移除支持向量机以外的所有训练数据，并且重新训练SVM，我们依然会得到相同的超平面。
• （5）一旦找到支持向量和最大边界超平面（MMH），则支持向量机模型就已经训练好了。
• （6）支持向量可用来计算SVM预期分类错误率的边界，因此分类错误率与数据维度、数据总量无关，只与支持向量的数量有关，因此一个支持向量数量稀少的SVM分类器，即使面对信息的维度十分高时，其泛化能力（Generalization）仍然会很好。
• （7）可构建复杂的非线性决策边界，SVM具有极高的正确率。
• （8）在建模时，不使用全量数据，而是从数据中挑选出支持向量（Support Vector）再建立模型，其复杂度取决于支持向量的数目，而不是全信息的数量，因此SVM很少出现过拟合情况。
• （9）分割线具有一个标准：对于之前未见到的数据，能具有最小分类错误率。
• （10）训练模型阶段，SVM就是在寻找具有最大边界的超平面（Maximum Marginal Hyperplane）.

　　  

3.SVM如何处理线性不可分

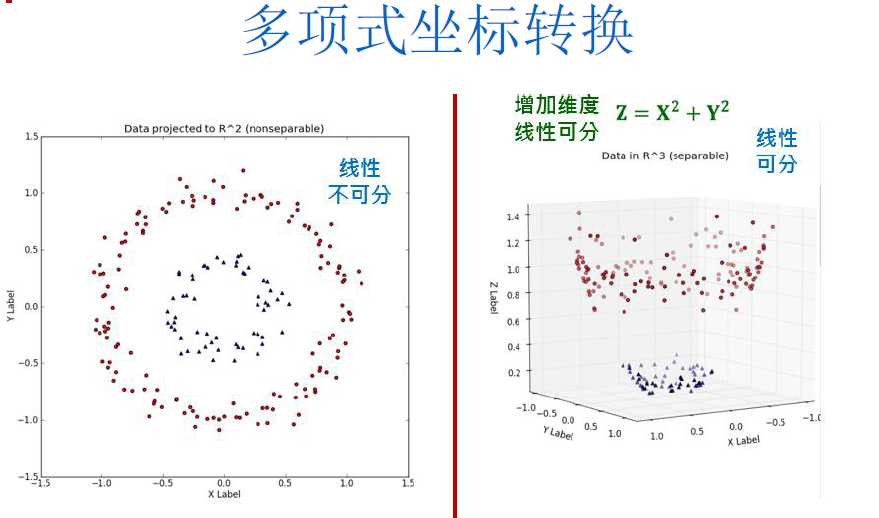
　　第一步：使用一个非线性转化，将原始数据映射至较高维度的特征空间（Feature Space）,此步骤，可以有许多的映射函数供使用，我们称此映射函数为“核函数（Kernel Function）”，不同的核函数的训练结果，会对应到输入空间上不同类型的非线性分类器。

　　第二步，在高维度特征空间中找出最佳的线性分割平面，，此时在高维度特征空间中找到的最大边界超平面（MMH），对应至原来空间就是一个非线性分割曲面或者曲线。

 

4.SVM常用的核函数

• 多项式转换(Polynomial Kernel)
• 高斯RBF转换(Gaussian Radial Basis Function)
• Sigmoid转换(Sigmoid Kernel)

 

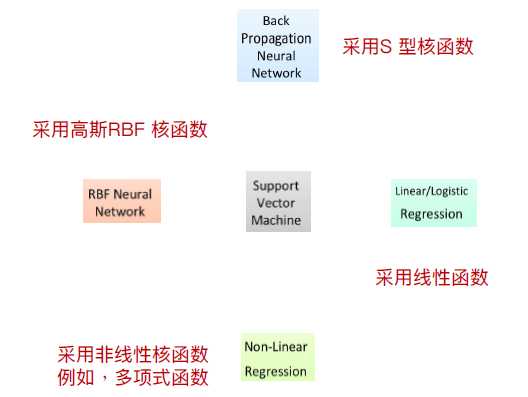
5.SVM与逻辑回归、神经网络、非线性回归间的关系

　　SVM使用高斯RBF核函数（Gaussian Radial Basis Function）所找到的分类器与RBF类神经网络相同

　　SVM使用S型核函数（Sigmoid Kernel）所找到的分类器等同于BP类神经网络。不同于类神经网络所使用的Bp算法通常会收敛到区域最佳解，SVM一定会找到全局最佳解。