动态规划 O（NlogN）结构

Posted 2020-12-14 et3-tsy

动态规划 O（NlogN）结构

在插入排序时，我们倘若用二分查找的形式去寻找插入位置，看似很快，但是却要移动后面的位置，使得这个二分得不偿失

但，如果只是替换某个值呢？

在动态规划的很多题目里面，我们正是要维护这样的一个决策单调序列，

进行更新采取的方案正是替换

注意，这样处理并不能记录opt答案对应的具体方案

---

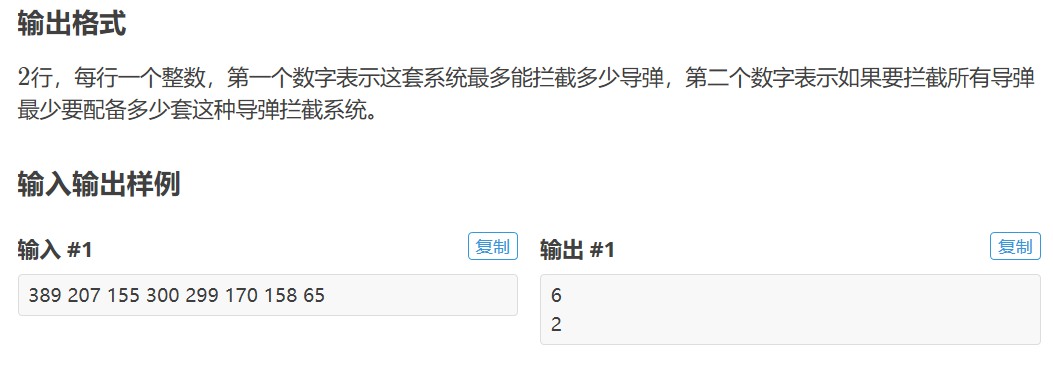
P1020 导弹拦截

https://www.luogu.com.cn/problem/P1439

#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>

using namespace std;

#define INF 1e10+5
#define MAXN 50005
#define MINN -100
int main()
{
    typedef long long int LL;
    cin.tie(0);
    ios::sync_with_stdio(false);

    vector<int>first;
    vector<int>second;
    vector<int>::iterator it;
    int cur2=MINN,cur1=MAXN;
    int curpos;
    int a;

    while(cin>>a)
    {

        if(cur1>=a)
        {
            first.push_back(a);
            cur1=a;
        }
        else
        {
            it=upper_bound(first.begin(),first.end(),a,greater<int>() );
            first.erase(it);
            first.insert(it,a);
            cur1=*(first.end()-1);
        }
        if(cur2<a)
        {
            second.push_back(a);
            cur2=a;
        }
        else
        {
            it=lower_bound(second.begin(),second.end(),a);
            second.erase(it);
            second.insert(it,a);
            cur2=*(second.end()-1);
        }


    }
    cout<<first.size()<<endl;
    cout<<second.size()<<endl;




    return 0;
}

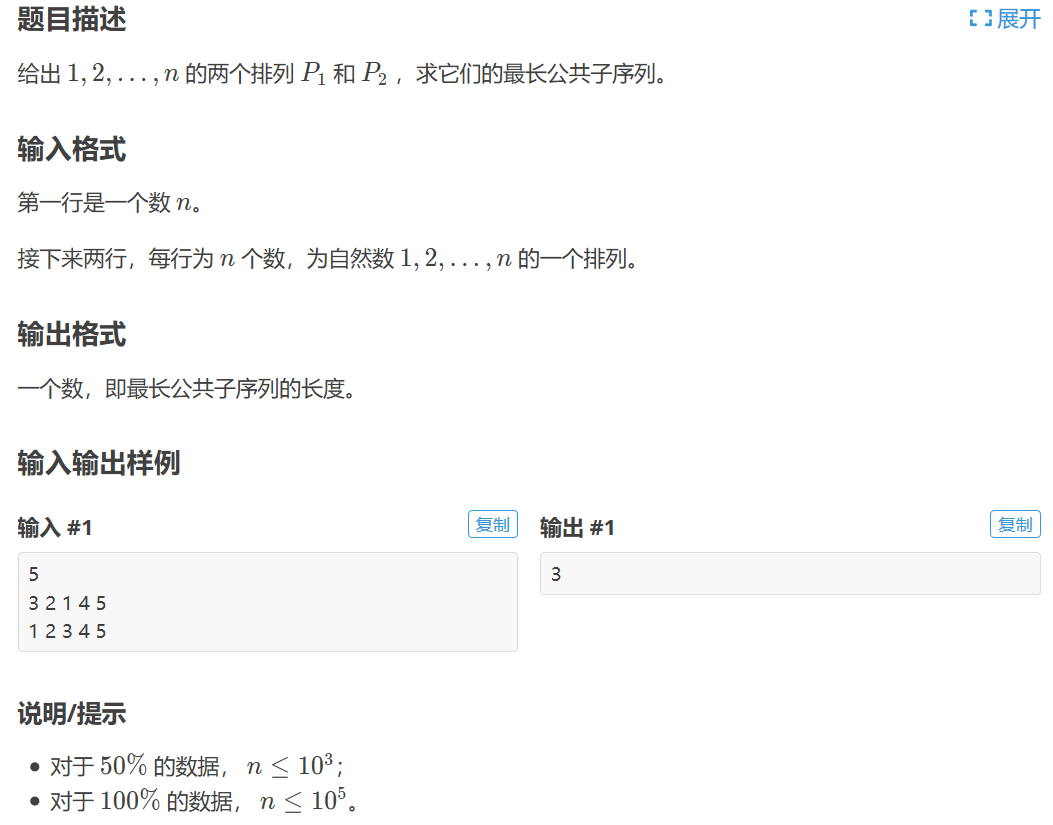
P1439 【模板】最长公共子序列

https://www.luogu.com.cn/problem/P1439

注意，这个LCS利用 O（NlogN）结构一定是在第一个序列里仅出现过一次

这个Dp核心是以大小的形式，记录一下某个字符或数字出现的位置，从而进行dp

#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
#define INF 0x3f3f3f3f
#define maxn 100005
#define minn -105
#define ll long long int
#define ull unsigned long long int
#define uint unsigned int
inline int read()
{
    int ans=0;
    char last=‘ ‘,ch=getchar();
    while(ch<‘0‘|ch>‘9‘)last=ch,ch=getchar();
    while(ch>=‘0‘ && ch<=‘9‘)ans=ans*10+ch-‘0‘,ch=getchar();
    if(last==‘-‘)ans=-ans;
    return ans;
}
int main()
{
    int n,cur;
    int pos[maxn];
    vector<int>line;
    n=read();
    for(int i=1;i<=n;i++)
    {
        cin>>cur;
        pos[cur]=i;
    }
    for(int i=1;i<=n;i++)
    {
        cin>>cur;
        cur=pos[cur];
        if(line.empty())
        {
            line.push_back(cur);
            continue;
        }
        if(cur>line[line.size()-1])
        {
            line.push_back(cur);
            continue;
        }
        vector<int>::iterator curpos=upper_bound(line.begin(),line.end(),cur);
        line.erase(curpos);
        line.insert(curpos,cur);
    }
    cout<<line.size();
    return 0;
}