算法漫游指北（第十三篇）:二叉树的基本概念满二叉树完全二叉树二叉树性质二叉搜索树二叉树定义二叉树的广度优先遍历

Posted 2020-12-14 nicholas0707

一、二叉树

二叉树的基本概念

二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。

 

两种特殊的二叉树

满二叉树（Full Binary Tree）

一棵满二叉树就是高度为k，且拥有(2^k)-1个节点的二叉树，一棵满二叉树每个节点，要么都有两棵子树，要么都没有子树；而且每一层所有的节点之间必须要么都有两棵子树，要么都没子树。

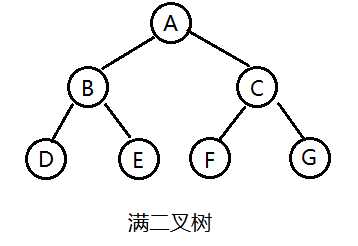
完全二叉树（Complete Binary Tree）

完全二叉树是一颗特殊的二叉树，它遵循以下规则： 假设完全二叉树高度为k，则完全二叉树需要符合以下两点： 1）所有叶子节点都出现在k层或k-1层，并且从1~k-1层必须达到最大节点数。 2）第k层可以是不满的，但是第k层的所有节点必须集中在最左边。

 

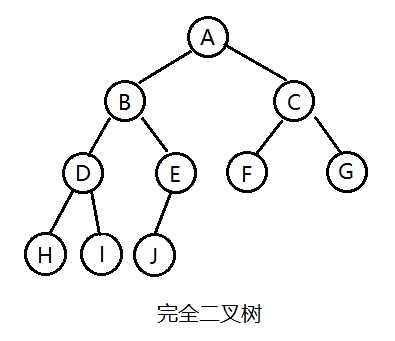
“完全”和“满”的差异，满二叉树一定是完全二叉树，完全二叉树不一定是满的。

 

 

 

二叉树的性质

性质1:

在二叉树的第i层上至多有2^(i-1)个节点（i>0）

 

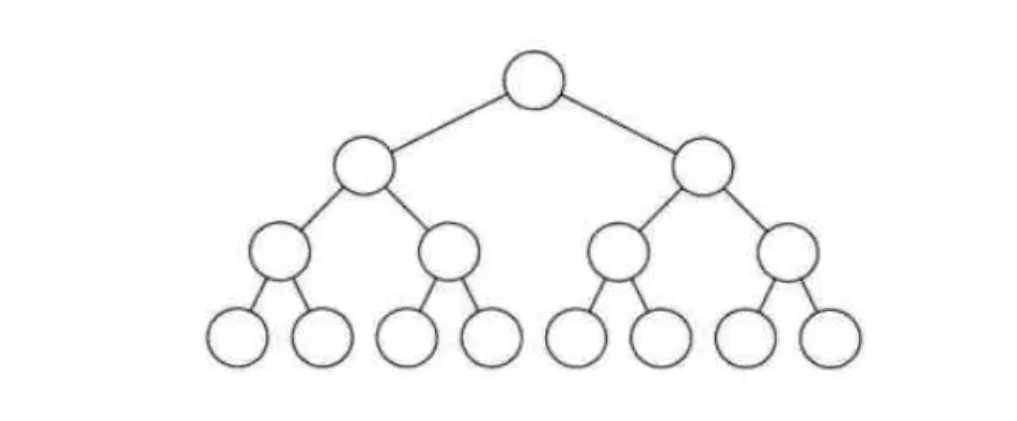
上图中： 第1层： 1个： 2^(1-1)=2^0=1

第2层： 1个： 2^(2-1)=2^1=2

第3层： 1个： 2^(3-1)=2^2=4

第4层： 8个： 2^(4-1)=2^3=8

通过数据归纳法，很容易得出在二叉树的第i层上最多有2^(i-1)个节点。

 

性质2:

深度为k的二叉树至多有2^k - 1个节点（k>0）

这里注意是2的k次幂再减1。

如果有一层，最多1=2^1-1个节点

如果有两层，最多1+2=2^2-1个节点

如果有三层，最多1+2+4=2^3-1个节点

如果有四层，最多1+2+4+8=2^4-1个节点

通过数据归纳法的论证，可以得出如果有k层，节点数最多为2k-1。

性质3:

对于任意一棵二叉树，如果其叶节点数为N0，而度数为2的节点总数为N2，则N0=N2+1;

终端节点就是叶子节点，而一棵二叉树，除了叶子节点外，剩下的就是度为1和2的节点了，设n1是度为1的节点数。则树T的节点总数就是n=n0+n1+n2。

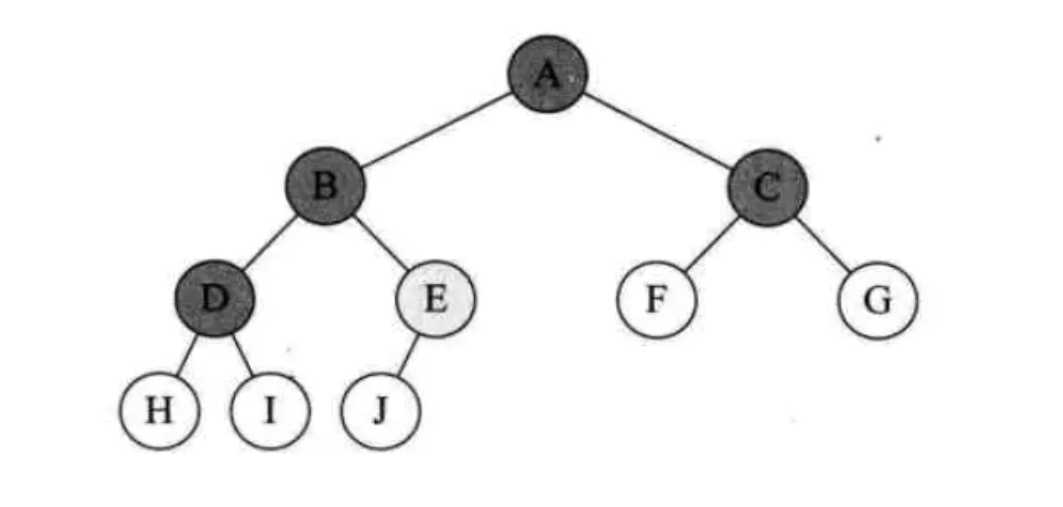
若度为1的节点有 n1个，总节点个数为n，总边数为 e，则根据二叉树的定义，

n=n0+n1+n2

总边数等于每个节点都有一个边，但是根节点有两个，所以e = n-1。

计算总边数的第二种方式，总边数 = 度数为2的节点数乘以2（因为这个节点有2个边）+加上度数为1的节点数

即 e = n1+2n2.

e = n1+2n2= n-1 (方程式1)

n=n0+n1+n2(方程式2)

两个方程式联合得到结果，

移动方程式1，n=n1+2n2+1 (方程式3)

方程式2与方程式2相减，得到结果 0 = n0 -n2-1

即N0=N2+1

性质4:

具有n个节点的完全二叉树的深度必为 log2(n+1)

对性质1结论进行取对数。

 

性质5:

如果对一棵有n个节点的完全二叉树的节点按层序编号（从第一层到最后一层，每层从左到右），对任一节点i（1<=i<=n）有：

1. 如果i=1，则节点i是二叉树的根，无双亲；如果i>1，则其双亲是节点 ⌊ i/2 ⌋ 。

2. 如果2i>n，则节点i无左孩子（节点i为叶子节点）；否则其左孩子是节点2i 。

3. 如果2i+1>n，则节点i无右孩子；否则其右孩子是节点2i+1 。

 

二叉搜索树定义

  

二叉搜索树(BST)是二叉树的一种，但是它只允许你在左侧节点存储(比父节点)小的值， 在右侧节点存储(比父节点)大(或者等于)的值。

二叉搜索树(Binary Search Tree)，又名二叉排序树(Binary Sort Tree)。   二叉搜索树是具有有以下性质的二叉树：   （1）若左子树不为空，则左子树上所有节点的值均小于或等于它的根节点的值。   （2）若右子树不为空，则右子树上所有节点的值均大于或等于它的根节点的值。   （3）左、右子树也分别为二叉搜索树。

 

二叉树的节点表示以及树的创建

通过使用Node类中定义三个属性，分别为elem本身的值，还有lchild左孩子和rchild右孩子

class Node(object):
    """节点类"""
    def __init__(self, elem, lchild=None, rchild=None):
        self.elem = elem
        self.lchild = lchild
        self.rchild = rchild

#树的创建,创建一个树的类，并给一个root根节点，一开始为空，随后添加节点
class Tree(object):
    """树类"""
    def __init__(self, root=None):
        self.root = root
?
    def add(self, elem):
        """为树添加节点"""
        node = Node(elem)
        #如果树是空的，则对根节点赋值
        if self.root == None:
            self.root = node
            return
        queue = []
        queue.append(self.root)
        #对已有的节点进行层次遍历
        while queue:
            #弹出队列的第一个元素
            cur = queue.pop(0)
            if cur.lchild == None:
                #如果左子树为空，则加到左子树上
                cur.lchild = node
                return
            elif cur.rchild == None:
                #如果右子树为空，则加到右子树上
                cur.rchild = node
                return
            else:
                #如果左右子树都不为空，加入队列继续判断
                queue.append(cur.lchild)
                queue.append(cur.rchild)

　　

　　

二叉树的遍历

树的遍历是树的一种重要的运算。所谓遍历是指对树中所有节点的信息的访问，即依次对树中每个节点访问一次且仅访问一次，我们把这种对所有节点的访问称为遍历（traversal）。那么树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先一般用递归，广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现(掌握先序、中序、后序的非递归方式)。

 

二叉树的广度优先遍历(层次遍历)

从树的root开始，从上到下从从左到右遍历整个树的节点

 

    def breadth_travel(self):
        """广度遍历"""
        if self.root is None:
            return
        queue = [self.root]
        #这里的队列也可以用python标准库中的collections中的queue
        while queue:
            cur_node = queue.pop(0)
            print(cur_node.elem, end=" ")
            if cur_node.lchild is not None:
                queue.append(cur_node.lchild)
            if cur_node.rchild is not None:
                queue.append(cur_node.rchild)
 

　　

 

 

参考资料

[1]https://juejin.im/post/5ae91ac9f265da0b83368aec

[2]<<大话数据结构 >>