决策变元选择_决策分支策略——文献学习SAT Solving with Reference Points

Posted 2020-12-13 yuweng1689

要点：使用DMRP algorithm (decision making with a reference point)在重启阶段为解决问题提供好的方向。

引文来自：

Kottler S. (2010) SAT Solving with Reference Points. In: Strichman O., Szeider S. (eds) Theory and Applications of Satisfiability Testing – SAT 2010. SAT 2010. Lecture Notes in Computer Science, vol 6175. Springer, Berlin, Heidelberg

 

---

 

Abstract

Many state-of-the-art SAT solvers use the VSIDS heuristic to make branching decisions based on the activity of variables or literals. In combination with rapid restarts and phase saving this yields a powerful decision heuristic in practice. However, there are approaches that motivate more in-depth reasoning to guide the search of the SAT solver. But more reasoning often requires more information and comes along with more complex data structures. This may sometimes even cause strong concepts to be inapplicable in practice. 译文：然而，有一些方法可以激发更深入的推理来指导SAT求解器的搜索。 译文：但更多的推理往往需要更多的信息，并伴随着更复杂的数据结构。这有时甚至可能导致强概念在实践中不适用。

In this paper we present a suitable data structure for the DMRP approach to overcome the problem above. Moreover, we show how DMRP can be combined with CDCL solving to be competitive to state-of-the-art solvers and to even improve on some families of industrial instances. 译文：在本文中，我们提出了一个适用于DMRP方法的数据结构来克服上述问题。 译文：此外，我们还展示了如何将DMRP与CDCL解决方案结合在一起，以便与最先进的解决方案相竞争，甚至改进一些工业实例系列。

1 Introduction

Research in satisfiability checking (SAT) has managed to bridge the gap between theory and practice in many aspects. There are several kinds of real-world problems that are actually tackled by modelling those problems as SAT instances like hardware and software verification [21,10], planning [11], automotive product configuration [13] and haplotype inference in bioinformatics [15] (cf. [16]). 译文：可满足性检验的研究在许多方面弥补了理论与实践的差距。译文：通过将这些问题建模为SAT实例，实际上可以解决几种实际问题，如硬件和软件验证[21,10]、规划[11]、汽车产品配置[13]和生物信息学[15]中的单倍型推断(cf.[16])。

In the domain of SAT solving there are different schemes and even more variants of these schemes to decide whether there exists a satisfying assignment to the variables of a Boolean formula in CNF or if a formula cannot be satisfied by any assignment.译文：在SAT求解的领域中，有不同的方案，甚至这些方案的变种，以决定是否存在一个布尔公式的变量分配CNF或如果一个公式不能满足分配。 Both experiments and applications show that there is no perfect SAT solving approach that is suited for all different categories and families of problem instances. 译文：实验和应用表明，没有一种完美的SAT解决方法适合所有不同类别和家庭的问题实例。 However, conflict-driven solving has proven itself to be very successful on a wide range of benchmarks. In this paper we study the quite new DMRP algorithm (decision making with a reference point) [8,9] from a practical point of view. Moreover, a hybrid approach that combines DMRP and CDCL solving is presented which is also motivated by experimental evaluations.

The paper is organised as follows: In section 2 we sketch related work in the domain of CDCL and DMRP solving. Section 3 examines the DMRP approach from a practical point of view and we introduce a new implementation for this approach. 译文：从实用的角度研究了DMRP方法，并介绍了该方法的新实现。In section 4 we motivate the combination of CDCL and DMRP to a new hybrid approach. In section 5 some experimental results are presented.

2 Related Work

CDCL采用了从冲突赋值中学习的思想。

Conflict-Driven Solving. Conflict-driven solving with clause learning (CDCL) is a leading approach and is especially but not only successful for industrial problems. It is based on the GRASP algorithm [17] which extends the original DPLL branch-and-bound procedure [5,4] by the idea of learning from conflicting assignments. Moreover, conflicts are analysed to jump over parts of the search space that would cause further conflicts. 此外，对冲突进行分析，以跳过搜索空间中可能导致进一步冲突的部分。 There are several improvements to the original algorithm like the two-watched-literal data structure and the VSIDS (variable state independent decaying sum) variable selection heuristic [18]. In recent years further improvements have been achieved by developing different restart strategies like the concept of rapid and adaptive restarts [3,2] and so-called Luby restarts [14]. In combination with phase-saving [19] frequent restarts constitute a strong concept especially for industrial SAT instances. 此外，对冲突进行分析，以跳过搜索空间中可能导致进一步冲突的部分。

Decision Making with a Reference Point. DMRP is a new SAT solving approach that was proposed by Goldberg in [8,9]. Even though DMRP uses Boolean constraint propagation (BCP) with backtracking and learning from conflicting assignments it is not a simple variant of CDCL.译文：尽管DMRP使用布尔约束传播(BCP)来回溯并从冲突的赋值中学习，但它不是CDCL的一个简单变体。   In difference to CDCL solvers DMRP additionally holds a complete assignment (a so-called reference point). 译文：DMRP还持有一个完整的分配(一个所谓的参考点) The algorithm aims for modifying the current reference point P to P’ in order to satisfy a clause under consideration. 译文：该算法的目的是将当前参考点P修改为P’，以满足考虑中的一个子句。 Furthermore, it is crucial that all clauses being satisfied by P remain satisfied by the modified reference point P‘ . 译文：此外，至关重要的是，所有被P所满足的子句都必须被修改的参考点P’所满足。

Algorithm 1 gives an overview of the DMRP approach, though this notation varies in some ways from the original notation in [9].译文：算法1概述了DMRP方法，尽管这种表示法在某些方面与[9]中的原始表示法不同。 One invocation of the DMRP subsolver (line 7 of Algorithm 1) takes a clause and a reference point as arguments. 译文：对DMRP子解算器(算法1的第7行)的一次调用采用子句和引用点作为参数。   It may either compute a modification to the reference point or it may learn the empty clause or else it times out. 译文：它可以计算对参考点的修改，或者学习空子句，或者超时。 The latter case causes the surrounding algorithm to call the DMRP subsolver with another unsatisfied clause. 译文：后一种情况会导致周围的算法调用带有另一个不满意子句的DMRP子解算器。

3 A Closer Look at DMRP

 

 

4 Combining DMRP and CDCL to a Hybrid Solver

In Algorithm 1 we assume the initial reference point to be given from outside. In the original paper [9] reference points are chosen at random and are then tried to modify by a call to function solveDMRP. In case no result can be computed within a certain amount of time (i.e. number of conflicts) solveDMRP will be invoked with a new initial point. This is similar to local search restarts but with the difference that the DMRP algorithm itself carefully reasons on how to modify a reference point. However, the choices of initial points are crucial for the algorithm as presented in section 5.

As mentioned in section 2 CDCL solvers perform restarts quite frequently. At a restart activity values of variables or literals are kept and also a subset of the learned clauses is carried along for the next start. However, the current partial assignment (all literals in the trail) is almost completely rejected, even though phase saving keeps some information. This motivates a hybrid approach that reasonably alternates the CDCL and the DMRP algorithms. The DMRP approach offers a suitable possibility to take a closer look at the drawback of a partial assignment before it is rejected. It may focus on the not yet satisfied clauses.

Our recent implementation that is shown in Algorithm 3 combines both approaches by the use of the Luby et al. restart strategy [14] which proved itself successful in both theory and practice. The Luby strategy assumes that the algorithm does not have any external information and does not know when it is best to perform a restart. In that case the available computation time is shared almost equally among different restart strategies [14]. The function maxConflictCount in Algorithm 3 returns the number of conflicts for the next run due to the Luby strategy. That is the product of a constant factor f and the next number of the sequence (1, 1, 2, 1, 1, 2, 4, 1, 1, 2, 4, 8, 1,...) (see [14] for details).

The function chooseAlgo decides on which algorithm to use for the next run. On average we achieved the best results when running the DMRP algorithm exactly for the smallest conflict limit (when cl = f).

Since the DMRP algorithm requires a reference point i.e. an assignment to all variables the last partial assignment of the CDCL solver has to be extended to a complete assignment (extendPartialAssignmToRefPoint). This is done by continuing the previous CDCL search with the last partial assignment. However, within this execution only binary clauses are considered during search until all variables are assigned a value. This assignment constitutes the initial reference point for the DMRP algorithm. In this phase the solver may also realise that the formula is unsatisfiable. For the case the partial assignment is empty (at algorithm start) this function simply computes a reference point that satisfies all binary clauses. Taking care of binary clauses at first is also motivated by the work in [22] and [1] where the idea to primarily focus on binary clauses has also improved solving for some families of instances. This also guarantees an additional invariant for our data structure that a binary clause can neither be contained in the set M nor in the delta stack D (resp. its elements).

Some Adaptions for the Hybrid Approach

In addition to standard CDCL solving each clause of the formula is assigned an activity value initialised to zero at the beginning. Whenever a clause is involved in a conflict (i.e. it is used for resolution during the generation of a lemma) its activity value is increased. In some solvers (for instance [6]) this technique is common for learned clauses to clear the clause database of inactive learned clauses periodically. Our hybrid solver maintains an activity value for every clause.

This activity value of a clause is taken into account when the next clause from set M has to be chosen (line 6 of Algorithm 1) to be handled by the function dmrpTryModifyPoint. We always choose the clause with the highest activity value for the next attempt to modify the current reference point. However, if the call to dmrpTryModifyPoint times out or for two subsequent calls to solveDMRP the next clause with the second highest activity value is chosen.

In contrast to the original DMRP algorithm the conflict limit (timeout) for the function solveDMRP depends on the success of its subroutine dmrpTryModifyPoint in line 7 of Algorithm 1. If the current reference point could be improved the initial conflict limit is reset.

The solver also differs in the computation of the MakeCount of a variable. For the MakeCount one can count only the clauses currently in D to get the most local improvement or all clauses in D∪M can be considered to make decisions more globally. For variables that have the same MakeCount ties can be broken in favour of different issues which is explained in more detail in the next section.

 

 

 

5 Experiments and Evaluation

For the evaluation presented in this section we have run our solver for all industrial (application) instances of the SAT competitions resp. SAT Races of the years 2006 - 2009 that add up to 564 non-trivial4 instances. Each instance is preprocessed in advance and the timeout for the solvers was set to 1200 seconds. As a reference and also to check results we have run our CDCL solver using the Luby restart strategy (without DMRP) and MiniSAT 2.0 [6]. 译文：每个实例都被预先预处理，并且求解器的超时设置为1200秒。作为参考和检查结果，我们使用Luby重启策略(没有DMRP)和MiniSAT 2.0运行了CDCL求解器

Figure 3 shows the results of different configurations of the hybrid approach. Furthermore, there are results that show performance of a pure DMRP solver. The presented configurations differ in the following issues that are related to decision making: As mentioned above the MakeCount may consider all clauses in D∪M (global) or only clauses in D (local). If two variables have the same MakeCount ties are broken in favour of the variable v that: 译文：图3显示了混合方法的不同配置的结果。译文：提出的配置在以下决策相关的问题上有所不同: 译文：如上所述，MakeCount可以考虑D∪M(全局)中的所有子句，也可以只考虑D(局部)中的子句；两个变量具有相同的MakeCount情况下，依照变量的下述属性区分：

(Act)      has the highest activity value similar to the VSIDS heuristic [18]. 译文：(Act)  具有最高的活动值，类似于VSIDS启发式[18]   (BC)     has the smallest set R(v). This can be seen as a simple approximation of the BreakCount of the variable. In difference to the MakeCount the BreakCount of a variable v states the number of clauses that become unsatisfied by a flip of the value of variable v. 译文：这可以看作是对变量的BreakCount的简单近似。与MakeCount不同，变量v的BreakCount表示变量v的值翻转后不能满足的子句的数量。   (DC) was chosen least often for DMRP decisions. This avoids flipping always the same variables back and forth in different calls to solveDMRP. 译文：为DMRP决策选择最少的次数。这样就避免了在对solveDMRP的不同调用中总是来回翻转相同的变量。

The left plot of Figure 3 shows clearly that pure DMRP solving could not compete with CDCL solving. 译文：单纯的DMRP求解无法与CDCL求解相竞争。 Both pure DMRP configurations (global and local MakeCount) solve around 224 of 564 instances within 1200 seconds. Initial reference points are always chosen at random. Timeouts for the analysis of one reference point (one call to solveDMRP) are changed according to the Luby sequence. Modifying the strategy on how to choose initial reference points showed quite some impact. Our assumption was that DMRP requires a better guidance on where to start search and how to choose its initial reference points. That motivates our hybrid approach where DMRP gets its initial reference points indirectly from the CDCL solver. As the plots show this clearly improves the performance of the solver.

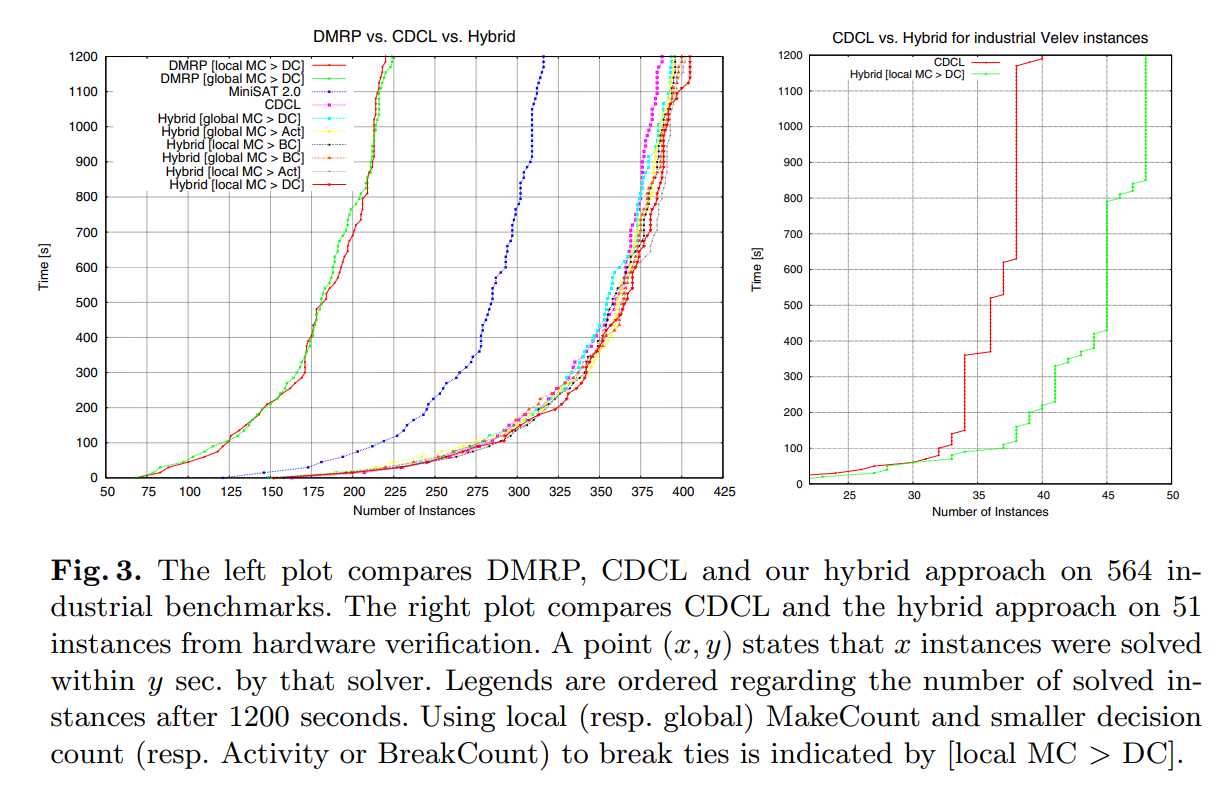Fig. 3. The left plot compares DMRP, CDCL and our hybrid approach on 564 industrial benchmarks. The right plot compares CDCL and the hybrid approach on 51 instances from hardware verification. A point (x, y) states that x instances were solved within y sec. by that solver. Legends are ordered regarding the number of solved instances after 1200 seconds. Using local (resp. global) MakeCount and smaller decision count (resp. Activity or BreakCount) to break ties is indicated by [local MC > DC].

A previous version of our hybrid approach [12] has taken part in the SAT competition 2009. That version mainly differs from the presented one regarding the restart strategy and the choice of when to perform DMRP resp. CDCL solving. It also implemented a more extensive solving of particular subsets of clauses which is only done for binary clauses in this improved approach. However, the results indicate that the older version did not utilize the DMRP approach in a sufficient way. Compared to MiniSAT 2.0 our hybrid approach also performs much better. Admittedly, this is not only due to the hybridisation with DMRP. This version of MiniSAT does neither use the Luby restart strategy nor phase saving. However, the hybrid approach also clearly outperforms our CDCL implementation with Luby restarts and phase saving.

The hybrid configuration where the MakeCount is computed locally outperformes the other configurations. It is interesting to notice that using the activity of variables to break ties does not achieve the best results. It turns out that it is better to prefer variables that were flipped least often at the current call of solveDMRP.

The right plot of Figure 3 compares pure CDCL with the hybrid approach on the 51 “Velev” instances of last years SAT competitions. For these instances that stem from the domain of hardware verification the hybrid approach clearly outperforms pure CDCL by solving 8 more instances.

Even though the hybrid implementation beats our pure CDCL solver on the entire benchmark set it turns out that for the most instances solved by the hybrid solver the answer was given by the CDCL part. Only about 6% were finally solved by the DMRP subsolver. Moreover, the improvement due to the hybridisation was mainly for unsatisfiable instances (17 more unsat results).

Our conjecture about this phenomenon is that DMRP generates some important lemmata: When the CDCL solver reaches the (current) maximum number of conflicts it delivers work to the DMRP solver. DMRP starts with an extension R of the last partial assignment P of the CDCL solver and hence focuses on a nearby part of the search space. When analysing this part it purposely examines clauses M that are not satisfied by R. In CDCL these clauses in M could likely become conflicting clauses if decisions were made similar to the values in R. Up to a certain point phase saving would do this after a normal CDCL restart. However, DMRP immediately considers clauses in M for search and resolution.

 

 

 

6 Conclusion

In this paper we have presented a data structure to implement the DMRP approach in an efficient way. Similar to the two-watched-literals scheme we choose one literal for each clause. The literal takes on responsibility so that a clause which is satisfied by a reference point is also satisfied by a modification of the point. Moreover, we present a way how to determine that variable which satisfies the most previously unsatisfied clauses when its value is flipped (MakeCount). Based on this implementation we motivate a hybrid SAT solver that combines CDCL and DMRP solving. Experiments have shown that our hybrid approach is competetive to the highly optimised state-of-the-art CDCL solvers and that the maintenance of complete assignments may definitely turn to account.

译文：在本文中，我们提出了一种数据结构来有效地实现DMRP方法。译文：与两种文字模式相似，我们为每个子句选择一个文字。译文：文字承担了责任，因此一个由参考点满足的子句也由该点的修改满足。 译文：此外，我们提出了一种方法来确定变量在其值被翻转时最满足之前未满足的子句(MakeCount)。译文：在此基础上，我们提出了一个结合CDCL和DMRP求解的混合SAT求解器。 译文：维持完成的赋值肯定会成为问题的关键。

 

 

 

 

 

 

References

1. 1.
   Bacchus, F.: Exploring the computational tradeoff of more reasoning and less searching. In: SAT 2002, pp. 7–16 (2002)Google Scholar
2. 2.
   Biere, A.: Adaptive restart strategies for conflict driven SAT solvers. In: Kleine Büning, H., Zhao, X. (eds.) SAT 2008. LNCS, vol. 4996, pp. 28–33. Springer, Heidelberg (2008)CrossRefGoogle Scholar
3. 3.
   Biere, A.: Picosat essentials. JSAT 4, 75–97 (2008)zbMATHGoogle Scholar
4. 4.
   Davis, M., Logemann, G., Loveland, D.: A machine program for theorem-proving. ACM Commun. 5(7), 394–397 (1962)MathSciNetCrossRefzbMATHGoogle Scholar
5. 5.
   Davis, M., Putnam, H.: A computing procedure for quantification theory. J. ACM 7(3), 201–215 (1960)MathSciNetCrossRefzbMATHGoogle Scholar
6. 6.
   Eén, N., Sörensson, N.: An extensible SAT-solver. In: Giunchiglia, E., Tacchella, A. (eds.) SAT 2003. LNCS, vol. 2919, pp. 502–518. Springer, Heidelberg (2004)CrossRefGoogle Scholar
7. 7.
   Fukunaga, A.S.: Efficient Implementations of SAT Local Search. In: SAT (2004)Google Scholar
8. 8.
   Goldberg, E.: Determinization of resolution by an algorithm operating on complete assignments. In: Biere, A., Gomes, C.P. (eds.) SAT 2006. LNCS, vol. 4121, pp. 90–95. Springer, Heidelberg (2006)CrossRefGoogle Scholar
9. 9.
   Goldberg, E.: A decision-making procedure for resolution-based SAT-solvers. In: Kleine Büning, H., Zhao, X. (eds.) SAT 2008. LNCS, vol. 4996, pp. 119–132. Springer, Heidelberg (2008)CrossRefGoogle Scholar
10. 10.
    Ivancic, F., Yang, Z., Ganai, M., Gupta, A., Ashar, P.: Efficient SAT-based bounded model checking for software verification. Theoretical Computer Science 404(3) (2008)Google Scholar
11. 11.
    Kautz, H.A., Selman, B.: Planning as satisfiability. In: Proceedings of the Tenth European Conference on Artificial Intelligence ECAI 1992, pp. 359–363 (1992)Google Scholar
12. 12.
    Kottler, S.: Solver descriptions for the SAT competition (2009), satcompetition.org
13. 13.
    Küchlin, W., Sinz, C.: Proving consistency assertions for automotive product data management. J. Automated Reasoning 24(1-2), 145–163 (2000)CrossRefzbMATHGoogle Scholar
14. 14.
    Luby, M., Sinclair, A., Zuckerman, D.: Optimal speedup of las vegas algorithms. In: ISTCS, pp. 128–133 (1993)Google Scholar
15. 15.
    Lynce, I., Marques-Silva, J.: SAT in bioinformatics: Making the case with haplotype inference. In: Biere, A., Gomes, C.P. (eds.) SAT 2006. LNCS, vol. 4121, pp. 136–141. Springer, Heidelberg (2006)CrossRefGoogle Scholar
16. 16.
    Marques-Silva, J.P.: Practical Applications of Boolean Satisfiability. In: Workshop on Discrete Event Systems, WODES 2008 (2008)Google Scholar
17. 17.
    Marques-Silva, J.P., Sakallah, K.A.: Grasp: A search algorithm for propositional satisfiability. IEEE Trans. Comput. 48(5), 506–521 (1999)MathSciNetCrossRefGoogle Scholar
18. 18.
    Moskewicz, M.W., Madigan, C.F., Zhao, Y., Zhang, L., Malik, S.: Chaff: engineering an efficient SAT solver. In: DAC (2001)Google Scholar
19. 19.
    Pipatsrisawat, K., Darwiche, A.: A lightweight component caching scheme for satisfiability solvers. In: Marques-Silva, J., Sakallah, K.A. (eds.) SAT 2007. LNCS, vol. 4501, pp. 294–299. Springer, Heidelberg (2007)CrossRefGoogle Scholar
20. 20.
    Selman, B., Levesque, H., Mitchell, D.: A new method for solving hard satisfiability problems. In: Tenth National Conference on Artificial Intelligence (1992)Google Scholar
21. 21.
    Velev, M.N.: Using rewriting rules and positive equality to formally verify wide-issue out-of-order microprocessors with a reorder buffer. In: DATE 2002 (2002)Google Scholar
22. 22.
    Zheng, L., Stuckey, P.J.: Improving SAT using 2SAT. In: Proceedings of the 25th Australasian Computer Science Conference, pp. 331–340. E (2002)Google Scholar