欧拉：数学中的网络问题——《费马大定理》

Posted 2020-12-13 ashleycom

欧拉

所有网络中的基本定理（网络公式），永恒关系式：

　　　　V + R - L = 1

其中

　　V=网络中顶点（即交点）的个数，

       L=网络中连线的个数

　　R=网络中区域（即围成的部分）的个数

欧拉宣称，对任何网络（所有可想象的网络 都服从欧拉公式的网络公式），将顶点和区域的个数加起来并减去连线的个数，其结果将总等于1.

 

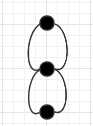
 顶点数=4

区域数=3

连线数=6

 

 

（a）              V+R-L=1+0-0=1

 

  (b)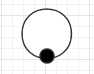    V+R+-L=1+1-1=1

 

  (c)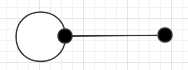    V+R-L=2+1-2=1

 

 

故，单点网络是对的，每增加一条信的连线会制造一个新的顶点或者新的区域。

 

 

欧拉提出，费马大定理的证明，能否先证明其中一个方程没有解，然后再对其他的方程推断这个结果，就如上述他对所有的网络证明网络公式时从最简单的情形（即单点网络）推广到其余情形那样。

 

费马

特殊形式的反证法：无穷递降法     证明了费马定理公式中4阶没有整数解。

假设，存在假定解，通过研究解的性质，费马能够证明：如果这个假定解确实存在，那么一定存在一个更小的解，然后通过再研究这个新解的性质，费马又能证明存在一个还要小的解，这样一直进行下去。

于是，费马找到了一列逐步递减的解，理论上它们将永远继续下去，产生越来越小的解，然而解必须是整数，因此这个永无止境的梯队是不可能存在的，因为它必定会有一个最小的可能解存在。这个矛盾证明了最初的关于存在一个解的假设一定是错的。

 

欧拉

欧拉试图以此为出发点