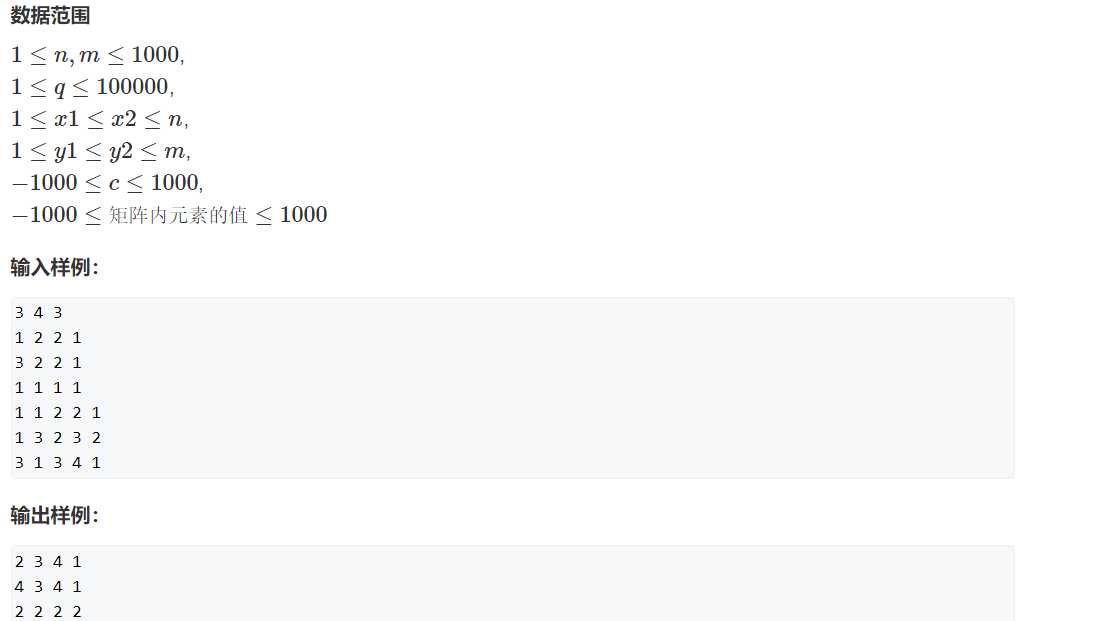
14.差分矩阵

Posted 2020-12-13 fx1998

 

 二维差分

原数组a[i][j]

差分数组b[i][j]

使得a数组是b数组的前缀和

同样开始时假定a[i][j]和b[i][j]都等于0

然后对于a数组中的每一个数再插一遍就好了

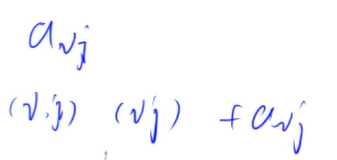
一维差分是对一段加上一个值

二维差分是对一个子矩阵加上一个值

b[x1][y1]加上c就是x1，y1右下角的所有点加上c

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 const int N = 1010;
 4 int a[N][N], b[N][N];
 5 //a是原矩阵
 6 //b是差分矩阵 
 7 void insert(int x1, int y1, int x2, int y2, int c) {
 8     b[x1][y1] += c;
 9     b[x2 + 1][y1] -= c;
10     b[x1][y2 + 1] -= c;
11     b[x2 + 1][y2 + 1] += c;
12 }
13 int main() {
14     int n, m, q;
15     cin >> n >> m >> q;
16     for (int i = 1; i <= n; i++) {
17         for (int j = 1; j <= m; j++) {
18             cin >> a[i][j];
19             insert(i, j, i, j, a[i][j]);
20         }
21     }
22     while (q--) {
23         int x1, y1, x2, y2, c;
24         cin >> x1 >> y1 >> x2 >> y2 >> c;
25         insert(x1, y1, x2, y2, c);
26     }
27     for (int i = 1; i <= n; i++) {
28         for (int j = 1; j <= m; j++) {
29             b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
30             cout << b[i][j] << " ";
31         }
32         cout << endl;
33     }
34     return 0;
35 }