图论算法 最短路SPFA算法

Posted zaza-zt

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了图论算法 最短路SPFA算法相关的知识，希望对你有一定的参考价值。

我可能要退役了……

退役之前，写一篇和我一样悲惨的算法：SPFA

最短路算法（二）SPFA算法

Part 1：SPFA算法是什么

其实呢，SPFA算法只是在天朝大陆OIers的称呼，它的正统名字叫做：队列优化的Bellman-Ford算法

在天朝，我们把它叫做“Shortest Path Fast Algorithm（SPFA）”翻译过来就是“快速最短路算法”

Part 2：SPFA算法的原理和实现思路

声明：以下的三元组(x,y,z)表示点 i ->点 j 有边权值为z，dis[x]表示出发点到编号为x节点距离

算法原理：

给定一张有向图，如果对于图中任意一条边(x,y,z)有 dis[y]<=dis[x]+z 成立，那么称这条边满足三角不等式

如果所有的边都满足三角不等式，则dis[x]就是出发点到x结点的最短路长度

正确性请读者自证（滑稽）

实现方法：

建立一个队列，最初队列里只有初始结点（假设为1）

取出队头节点x，扫描它的所有出边(x,y,z)，如果不满足三角不等式 (dis[y]>dis[x]+z)，更新 dis[y]=dis[x]+z，同时，如果此时 y 点不在队列中，把 y 点入队

重复上面的步骤，直到队列为空（此时所有边都满足三角不等式，得到单源最短路的解）

Part 3：SPFA算法性能、适用范围、初始化注意事项

上面说完了SPFA算法的思路框架，在看代码之前我们需要了解这些事项，来加深对这个算法的理解，避免在竞赛中使用错误的算法导致失分

1、适用范围：有向图、无向图、负权图，可以在出现负权回路时报错

该算法适用范围很广，值得一提的是：如果一个节点被入队了n（n是节点数）次，则图中存在负权回路

2、时间复杂度：

关于SPFA：

他死了

这个烂梗是怎么来的呢？其实这也是SPFA的死因——不稳定

很多编程的书上明确的写到：SPFA的时间复杂的为O（km），其中m是边数，k是小常数（约等于2）

很多童鞋就发现：“woc！这个算法不但可以处理负权图，负权回路可以报错，时间复杂度还小，真香啊！”

However，并不是这样的。。。有利必有弊，书中还有一句话很多人忽略掉了：

在特殊构造的图中，该算法复杂度很有可能退化

“退化”具体到什么程度呢？O（nm），其中n是节点数，m是边数，所以，对于某些特殊构造的完全图来说，用SPFA来实现最短路是很慢的（这个比n^2的复杂度还要高）

具体的能卡死SPFA的数据类似于这样：一开始诱导SPFA进入错误的最短路方向，先让他把整个图更新一遍，但是回头看，这个并不是最短路，于是再次花大量的时间进行重复更新，举个实例，链状+菊花状（网格图），这样构造的数据很容易就可以把SPFA卡死。

这里附上一位大佬的博客，里面有卡SPFA的思路，甚至还有hackSPFA数据生成器，有兴趣的朋友可以自己出一个题卡一卡SPFA，在这里我就不Copy了。https://blog.csdn.net/qq_45721135/article/details/102472101

不仅如此，更加丧心病狂的是：近几年出题人开始有意识的卡SPFA算法，导致很多SPFA算法的使用者失掉了分数，于是网上开始大传“SPFA已死”这样的评论

这里，我只能提醒大家一句我自己总结的规律：没有负权的最短路问题一定是在卡SPFA！

3、空间复杂度：

O（m），用邻接表没什么好说的

4、码长：

算法主体代码长度：约400B

整个求最短路代码长度：约950B

5、初始化注意事项：

dis[n]，记录最短路的数组初始化为0x3f，vis[n]，记录元素是否在队列里，初始化为0，另外，需要一个空的队列

Part 4：SPFA算法结构框架

这里给出我的程序，仅供参考，欢迎hack

#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstring>
#define N 101000
using namespace std;
typedef unsigned int unint;//闲的没事的typedef 
struct edge{
    int to,cost;//结构体构建邻接表 
};
vector<edge>v[N];//邻接表 
queue<int>q;//队列 
int dist[N],vis[N],n,m;
void spfa(int s)//s是起点 
{
    memset(dist,0x3f,sizeof(dist));//初始化距离无限大 
    memset(vis,0,sizeof(vis));//所有元素都不在队列里 
    dist[s]=0;//初始化起点距离是0 
    vis[s]=1;//起点在队列里 
    q.push(s);//起点入队 
    while(q.size()!=0)//队列不为空，执行循环 
    {
        int x=q.front();//取出队首 
        q.pop();
        vis[x]=0;//元素不在队列里 
        for(unint i=0;i<v[x].size();i++)//避免Dev警告，强迫症unint 
        {
            int y=v[x][i].to;//x点可以到的结点 
            int z=v[x][i].cost;//边的权值 
            if(dist[y]>dist[x]+z)//不满足三角不等式，进行更新 
            {
                dist[y]=dist[x]+z;
                if(vis[y]==0)//如果y不在队列里，入队 
                {
                    q.push(y);
                    vis[y]=1;
                }
            }
        }
    }
}

Part 5：用SPFA切题

https://www.luogu.com.cn/problem/P1339

由于我并不是SPFA算法的爱好者，所以我做题的时候能不用SPFA就不用SPFA，我翻了翻我之前的代码，发现SPFA竟然只有一份，那就放上来吧

技术图片

显然这是一个最短路的板子题

思路也很简单，先初始化好邻接表和起始点，终点，然后跑一边SPFA，输出dis[end]即可

下面上代码：

#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstring>
#define N 101000
using namespace std;
typedef unsigned int unint; 
struct edge{
    int to,cost; 
};
vector<edge>v[N]; 
queue<int>q; 
int dist[N],vis[N],n,m,st,end;
void spfa(int s) 
{
    memset(dist,0x3f,sizeof(dist)); 
    memset(vis,0,sizeof(vis)); 
    dist[s]=0;  
    vis[s]=1; 
    q.push(s); 
    while(q.size()!=0) 
    {
        int x=q.front(); 
        q.pop();
        vis[x]=0; 
        for(unint i=0;i<v[x].size();i++) 
        {
            int y=v[x][i].to; 
            int z=v[x][i].cost; 
            if(dist[y]>dist[x]+z) 
            {
                dist[y]=dist[x]+z;
                if(vis[y]==0) 
                {
                    q.push(y);
                    vis[y]=1;
                }
            }
        }
    }
}
int main()
{
    scanf("%d%d%d%d",&n,&m,&st,&end);//输入起始点和终点 
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);//初始化邻接表 
        v[x].push_back((edge){y,z});
        v[y].push_back((edge){x,z});
    }
    spfa(st);//以st为起点跑一边spfa 
    printf("%d",dist[end]);//输出dist[end]的值(st->end的最短路径)
    return 0;
}

Part 6：卡SPFA实况

为了防止一些同学不听我的忠告，下面对SPFA算法进行公开处刑（展示SPFA华丽丽的TLE）

https://www.luogu.com.cn/problem/P4779

技术图片

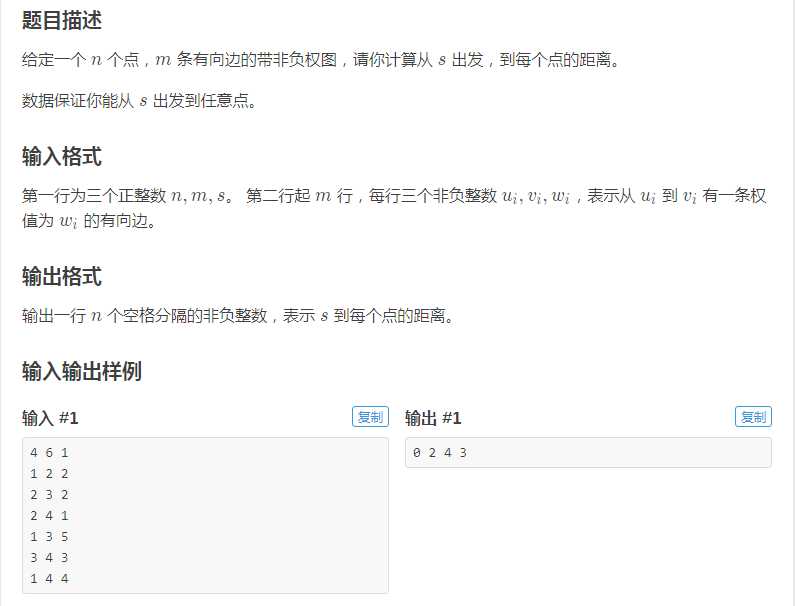
当时我一看这个题，woc这不就是一个板子题吗，直接贴了一个SPFA上去

正当我得意洋洋的看着正在评测，想着这题必A的时候，4个TLE让我傻眼了

技术图片

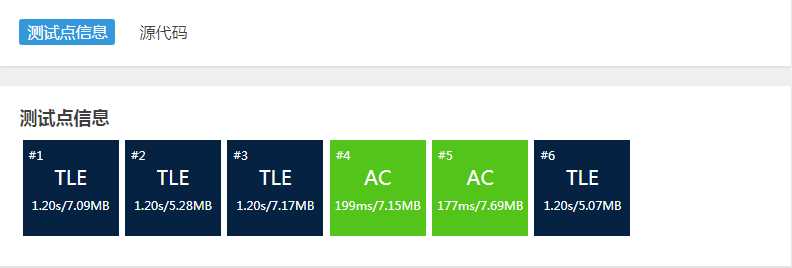
看了题解才知道要用Dijkstra+二叉堆优化才能过这个题。

本来还想写Dij算法的，但是我这波退役的匆忙，没有时间再写了，这里就把题解里的AC代码放上，大家自己理解吧……

话说这个大佬的邻接表和我的完全不一样啊喂……

#include<bits/stdc++.h>
#define M(x,y) make_pair(x,y)
using namespace std;
int fr[100010],to[200010],nex[200010],v[200010],tl,d[100010];
bool b[100010];
void add(int x,int y,int w){
    to[++tl]=y;
    v[tl]=w;
    nex[tl]=fr[x];
    fr[x]=tl;
}
priority_queue< pair<int,int> > q;
int main(){
    int n,m,x,y,z,s;
    scanf("%d%d%d",&n,&m,&s);
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
    }
    for(int i=1;i<=n;i++) d[i]=1e10;
    d[s]=0;
    q.push(M(0,s));
    while(!q.empty()){
        int x=q.top().second;
        q.pop(); 
        if(b[x]) continue;
        b[x]=1;
        for(int i=fr[x];i;i=nex[i]){
            int y=to[i],l=v[i];
            if(d[y]>d[x]+l){
                d[y]=d[x]+l;
                q.push(M(-d[y],y));//懒得重载运算符
            }
        }
    }
    for(int i=1;i<=n;i++) printf("%d ",d[i]);
    return 0;
}

Part 7：我为什么退役

顺便提一句，今天的正文部分到此就结束了，下面都是无关紧要的BB部分

考试过不了，考试过不了，考试过不了啊啊啊啊啊啊！！！！

6/27，这是沉重的一天，我参加了某推荐生考试，本来去了我所向往的高中之后，我就可以继续在OI的道路上越走越远的

但是，但是，我好像搞砸了。。。为了学OI和准备推荐生考试我花了很长时间，导致初中文化课没怎么复习，距离中考还有十几天，我还一点点都没有复习

本来这所高中就是重高，依靠中考很难考上，再加上我没有复习，直接原地爆炸

所以，综上这些原因导致了我OI梦的夭折，另外希望大家不要重蹈我的覆辙

最后，祝我退役快乐。。。。。

再见，或许……再也不见

以上是关于图论算法 最短路SPFA算法的主要内容，如果未能解决你的问题，请参考以下文章

图论算法最短路算法：Floyd算法！

图论算法最短路算法：Floyd算法！

最短路算法

图论最短路

小航的算法日记图论

OJ记录---图论最短路径问题，DFS，BFS，Dijistra，Dijistra+堆优化，SPFA