6.3符号的规则操作-图灵计算

Posted 2020-12-13 character2

6数学与计算

6.1语句与公式

6.2符号的模拟——算术

6.3符号的规则操作——计算

有了纸与笔，你掌握了乘法表与进位法，实际去笔算328*975，你不需要更多的考虑，你只需要用笔在纸上机械地操作就可以，这是数学的一个特征。再如简单的一元一次方程求解，其过程可固化为五个步骤：1根据等式性质去分母，2根据乘法分配律去括号，3根据等式性质移项，4根据乘法分配律合并同类项，5系数化为1。机械的操作是都是根据形式决定的，恰当的符号让形式更清晰、易理解。

上世纪三十年代，英国数学家图灵（Alan Mathison Turing，1912.6-1954.6）在对人用笔在纸上进行计算的过程进行了仔细的考察，提出了图灵机的概念。图灵机是抽象计算机的模型，其基本原理并不复杂。

 

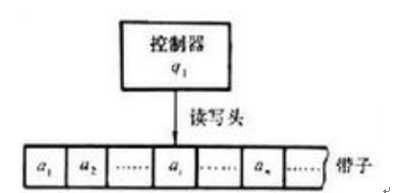
图灵机的机械部分包括：

1输入的纸带（用于输入与输出，关键词：无限长）：

可以设想为一个无限长的纸带，纸带分为一个个单元格，每个单元格上记录某个字符表中的一个字符a。

2读写头

读写头可以在纸带上左右移动，其作用是：

读取当前单元格里的字符，

擦除当前单元格里的字符

将一个字符写入当前单元格

任意时刻读写头只能在一个单元格上操作。

图中的控制器可分解为下面的逻辑部件：

3字母表

字母表包括了输入纸带单元格上可以有的字符，读写头可以写入单元格的字符，比如字符集是{“1”、“0”、“+”、“=”、“︺”}。

4状态集

图灵机在任意时刻都处于一种状态下，所有的状态构成状态集{s0、s1、s2、s3、s4、s5}，这其中包括

开始状态s0：每次运行的开始都处于此状态

停机状态s5：当图灵机进入此状态时，机器就停止运行，此状态下纸带留下的字符就为计算结果

5控制规则

读写头读取当前单元格的字符，结合当前机器的状态，可决定：

一：图灵机的新状态

二：图灵机的响应操作

  擦除：擦除当前单元格的内容

  写入：在当前单元格写入字符集中的一个字符

  移动：向左或向右

图灵机的操作可抽象为：（（当前状态、当前读入）—>（新状态、当前写入、移动方向））。我们构造个简单的例子，这个例子是二进制个位的加法运算。设计七种状态：，

s0：初始状态

s1：被加数=1

s2：被加数=0

s3：被加数、加数=1

s4：被加数、加数不一致

s5：被加数、加数=0

S6: 停机状态

字符表为{“1”、“0”、“+”}，

擦除操作表示清空单元格内容。

可制定的规则如下：

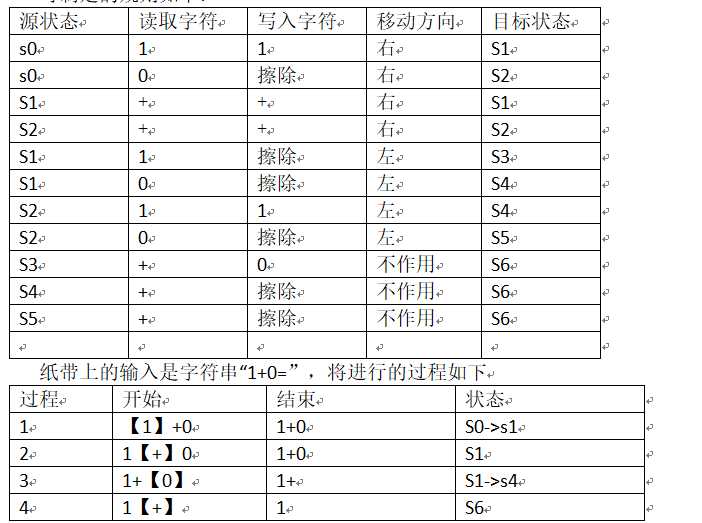
这是个简单的例子。正是所能见到的例子都过于简单，人们反倒不理解图灵机能有什么用。你看到的实际计算机对复杂问题的处理，比如宇宙演化的模拟，天气预报等，其所应用的是同样原理，不同在于字符集、状态集、控制规则的数量级。图灵机的强大还在于可以构造通用图灵机：可以模拟其它图灵机的图灵机。一台解决特定问题的图灵机，其字符集、状态集、控制规则的数量始终是有限的，因此它所有（（当前状态、当前读入）—>（新状态、当前写入、移动方向））可以以某种方式编码，作为另一台图灵机纸带上的特定输入，同时它运行时的状态、位置也在模拟时维护在特定单元格，这样后一台图灵机通过读取上的控制可以按前一台图灵机的算法去运行。通用图灵机的概念也就是后来“可存储程序计算机”的思想。目前已知最小的通用图灵机是是字符表的字符数量为2，状态集的状态数量为3的图灵机，这比上面举例还要简单，理论上今天所有计算机的能力都不能超过这台最小的通用图灵机，差别只在于效率上。

提出图灵机思想的论文题目是“论数字计算在决断难题中的应用”，图灵所要解决的问题首先是数的可计算问题，比如圆周率(π)，是否能计算到它的任意一位。问题的直接背景是希尔伯特第十问题。1900年新世纪开始时，德国数学家希尔伯特在巴黎第二届国际数学家大会上作了《数学问题》的著名讲演，提出了数学理论中23个最困难的问题，后来这个世纪的数学进展与这23个问题解决密切相关。其中的第10个问题也称为判定性问题。原题目是：给定一个系数均为有理整数，包含任意多个未知数的丢番图方程：设计一个过程，通过有限次的计算，能够判定该方程在有理数上是否可解。问题的一般形式是：存在或不存在对任何可定义的数学问题可解的判定方法？从数的可计算去研究是个策略，数的可计算是个技术细节更单纯的问题，同时图灵证明了此问题与逻辑上可判定问题等价。

按照图灵的研究，一个数学问题的可计算等于此问题的图灵机可计算，可计算的数是无限可数，不可计算数无限且不可数，现代集合论的说法：后者的阶高于前者。希尔伯特的判定问题可归为一台通用图灵机不通过实际模拟另一台图灵机，是否可判定另一台图灵机会停机，图灵的答案是否定，这样希尔伯特的判定问题无解的，同时这也说明了图灵机的局限。在图灵完成其论文几个月前，美国数学家阿隆佐·邱奇(Alonzo Church：1903.6–1995.8)提交了论文“关于判定性问题的解释”，同样证明了判定性问题无解。邱奇所采用的方法是基于递归函数与Lambda运算来论证的。

图灵机的基本原理虽然简单，背后涉及的问题足够深刻，很多的讨论一直延续至今，并将持续下去。这些讨论可归结到三个基本的问题：人的大脑是不是一台图灵机？宇宙是不是一台图灵机？在不违背物理规律的情况下，能不能设计出超过通用图灵机的机器？

从本书的主题，图灵机是从刻画了人用笔在纸上的计算过程开始的。图灵机的读写头相当于人的眼睛与手，纸带输入是求解的问题，根据输入以及当前的状态，产生新的状态并匹配适用的规则进行写入与移动操作，这与人用笔在纸上计算时的决策与操作是一致的。图灵机的原子操作是：读取一个字符，删除字符，写入一个字符，单元格已有字符时再写入可视为修改，人类符号应用中媒介物理层面的原子操作同样如此，可能有些不同之处，如删除不一定是清除，而是划线作废，修改是作废后在旁边位置补写正确的符号，这种差异并无实质的意义。

图灵机对计算进行了一般化的抽象：广义的计算就是基于规则的符号机械操作。在此定义下，只要有确定的规则，图灵机都可以执行计算。这超出了数学里的计算概念，事实上现代计算机应用主要也不是数学上算式的求解，所操作的符号也不限于数值符号。还有哪些形式的计算？它们来自哪里？图灵的理论没有描述，今天 这被默认一种开放式的应用，这种应用足够普及且成功。结合前面图灵机延伸出的三个问题，计算虽然起源于数学，但在今天可看到的趋势是：计算概念可以不依赖数学，反过来可以认为数学依赖于计算概念，计算看作是一个独立的范式，或一种哲学。没有改变的是：这仍是对符号的操作。

（作者（LQS）注：连续地阅读会发现，系列的文章不是对各个问题的解释，而是新的理解视角）