题解 Accumulation Degree

Posted 2020-12-12 lcguo

【题目描述】

有一个有 (n) 个节点，(n-1) 条河道的树形水系。

每个河道有一个最大容水量 (c[x][y]) 表示点 (x) 到 (y) 的最大容水量.

源点可以源源不断出水，以源点作为根节点的树的叶子结点可以无限接纳水。

而一个节点水的流量等于流过其儿子节点的水的流量之和，儿子节点水的流量不能超过其与父亲连边的最大容水量，询问最大的源点水流量。

【输入格式】

输入的第一行是整数 (T)，表示测试用例的数量。

每个测试用例的第一行是正整数 (n)。

以下 (n-1) 行中的每一行包含由空格分隔的三个整数 (x,y,z)，表示在节点 (x) 和节点 (y) 之间存在边，并且边的容量为 (z)。

节点编号从 (1) 到 (n)。

【输出格式】

对于每个测试用例，将结果输出到一行。

【样例输入】

1
5
1 2 11
1 4 13
3 4 5
4 5 10

【样例输出】

26

【数据规模与约定】

所有的输入均为正整数，且不超过 (2 imes10^5)。

---

我们先考虑 (O(n^2)) 的暴力，我们设 (g_i) 表示以 $i $ 为根节点的子树中，以 (i) 为源点，从 (i) 出发流向子树的流量的最大值。

(degree(x)) 表示 (x) 的度数。

所以

[g_x=sumlimits_{yin Son(x)}Large{_{c(x,y) degree(y)=1}^{min(g_y,c(x,y)) degree(y)>1} ]

我们可以枚举每个源点 (s)，并每次用树形 dp 在 (O(n)) 的时间内求出 (g_s)，所以总时间复杂度是 (O(n^2)) 的。

然后可以用 ”二次扫描与换根法“ 在 (O(n)) 的时间结局这个问题。

我们先任选一个点 (root) 作为根，然后根据上面的转移方程来求出 (g) 数组。

设 (f_i) 表示以 (i) 为根，流向整颗树的流量的最大值，有 (f_{root}=g_{root})。

我们假设 (f_x) 以及被求出，考虑他的子节点 (y)。

(f_y) 分为两部分，向子树的流量和向 (x) 的流量，如图：

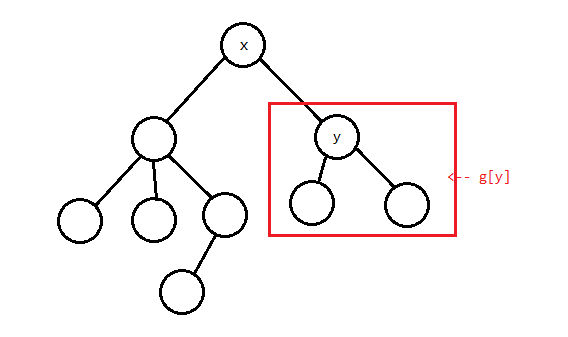
向子树的流量就是 (g_y)；因为以 (x) 为源点的最大流量是 (f_x)，(x o y) 的最大流量是 (min(c(x,y),g_y))，所以从 (x) 流向其他子树的最大流量是 (f_x-min(c(x,y),g_y))，可以得到：

[f_y=d_y+Large{_{c(x,y) degree(x)=1}^{min(f_x-min(c(x,y),g_y),c(x,y)) degree(x)>1} ]

然后两次 ( ext{dfs}) 就解决了，代码如下：

#include<bits/stdc++.h>
#define rint register int
using namespace std;
inline int read(){
    int s=0,f=1; char c=getchar();
    while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=0;c=getchar();}
    while(c>=‘0‘&&c<=‘9‘) s=(s<<1)+(s<<3)+(c^48),c=getchar();
    return f?s:-s;
}
int n,f[200010],g[200010],vis[200010],ind[200010],ans(-1);
int tot,head[200010],nxt[400010],ver[400010],edge[400010];
void add(int x,int y,int v){
    nxt[++tot]=head[x]; ver[tot]=y;
    head[x]=tot; edge[tot]=v;
}
void dfs_first(int x){
    vis[x]=1; g[x]=0;
    for(rint i=head[x];i;i=nxt[i]){
        int y=ver[i],v=edge[i];
        if(vis[y]) continue;
        dfs_first(y);
        if(ind[y]==1) g[x]+=v;
        else g[x]+=min(v,g[y]);
    }
}
void dfs_second(int x){
    vis[x]=1;
    for(rint i=head[x];i;i=nxt[i]){
        int y=ver[i],v=edge[i];
        if(vis[y]) continue;
        if(ind[x]==1) f[y]=g[y]+v;
        else f[y]=g[y]+min(f[x]-min(v,g[y]),v);
        dfs_second(y);
    }
}
int main(){
    int T=read();
    while(T--){
        memset(head,0,sizeof head);
        memset(vis,0,sizeof vis);
        memset(ind,0,sizeof ind);
        tot=0; n=read();
        for(rint i=1;i<n;++i){
            int x=read(),y=read(),v=read();
            add(x,y,v); add(y,x,v);
            ++ind[x]; ++ind[y];
        }
        dfs_first(1);
        memset(vis,0,sizeof vis);
        f[1]=g[1]; ans=-1;
        dfs_second(1);
        for(rint i=1;i<=n;++i) ans=max(ans,f[i]);
        printf("%d
",ans);
    }
    return 0;
}