多源对多源最短路

Posted 2020-12-12 spnooyseed

https://ac.nowcoder.com/acm/contest/6116/B
魔方国有n座城市，编号为1sim n1～n。城市之间通过n-1条无向道路连接，形成一个树形结构。
在若干年之后，其中p座城市发展成了大都会，道路的数量也增加到了m条。
大都会之间经常有贸易往来，因此，对于每座大都会，请你求出它到离它最近的其它大都会的距离。

蒟蒻第一次见多源对多源最短路，没想到是这种处理方式。

1. 第一步就是按照正常加一个虚点连接所有的大都会，距离为0然后跑一边dijkstra ， 同时记录当前这个点距离哪个大都会最近。
2. 当前u点最近的大都会from[u] , v点最近的大都会from[v] ,
   如果他们from[u] = from[v] ， 那也就是u 和 v两点由同一个点拓展而出 ， 否则的话由两个点拓展而出的时候，就可以算一下这两个拓展点之间的最短距离 ，，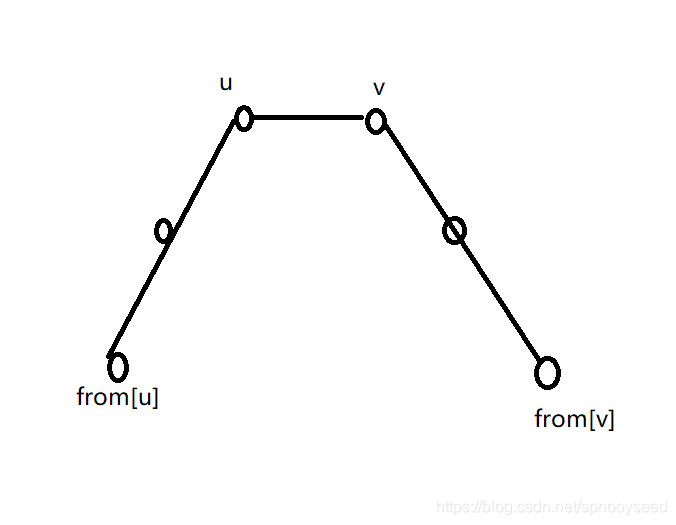
   那么其中一个大都会距离另一个大都会的最短距离可更新为ans = min(ans , dis[u] + dis[v] + w )

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
#include <vector>
#include <map>
#include <list>
#include <queue>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <stack>
#include <set>
#pragma GCC optimize(3 , "Ofast" , "inline")
using namespace std ;
#define ios ios::sync_with_stdio(false) , cin.tie(0) , cout.tie(0)
#define x first
#define y second
typedef long long ll ;
const double esp = 1e-6 , pi = acos(-1) ;
typedef pair<ll , ll> PII ;
const int N = 1e6 + 10 , INF = 0x3f3f3f3f , mod = 1e9 + 7;
ll in()
{
  ll x = 0 , f = 1 ;
  char ch = getchar() ;
  while(!isdigit(ch)) {if(ch == ‘-‘) f = -1 ; ch = getchar() ;}
  while(isdigit(ch)) x = x * 10 + ch - 48 , ch = getchar() ;
  return x * f ;
}
int e[N] , ne[N]  , h[N] , n , m , p , idx , a[N]  , vis[N] , from[N] ;
ll dis[N] , ans[N] , w[N] ;
void add(int a , int b , int c)
{
  e[idx] = b , ne[idx] = h[a] , w[idx] = c , h[a] = idx ++ ;
}
int main()
{
  memset(h , -1 , sizeof h) ;
  n = in() , m = in() , p = in() ;
  for(int i = 1; i <= p ;i ++ ) a[i] = in() ;
  for(int i = 1 , a , b , c ; i <= m ;i ++ )
   a = in() , b = in() , c = in() , add(a , b , c) , add(b , a , c) ;

  for(int i = 1 ; i <= n ;i ++ ) ans[i] = dis[i] = 1e18 ;
  priority_queue<PII , vector<PII> , greater<PII> > q ;
  for(int i = 1; i <= p ;i ++ )
   q.push({0 , a[i]}) , dis[a[i]] = 0 , from[a[i]] = a[i] ;
  while(q.size())
  {
    auto t = q.top() ;q.pop() ;
    if(vis[t.second]) continue ;
    vis[t.second] = 1 ;
    int u = t.second ;
    for(int i = h[u] ; ~i ; i = ne[i])
     {
       int v = e[i] ;
       if(dis[v] > dis[u] + w[i])
        dis[v] = dis[u] + w[i] , from[v] = from[u] , q.push({dis[v] , v}) ;
       else if(from[v] != from[u])
        {
          ll t = dis[u] + dis[v] + w[i] ;
          ans[from[v]] = min(ans[from[v]] , t) ;
          ans[from[u]] = min(ans[from[u]] , t) ;
        }
     }
  }
  for(int i = 1; i <= p ;i ++ ) cout << ans[a[i]] << " " ;
  puts("") ;
  return 0 ;
}
/*
*/