P1600 天天爱跑步

Posted 2020-12-12 zzyh

题目描述

小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。«天天爱跑步»是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。

这个游戏的地图可以看作一一棵包含 nn个结点和 n-1n−1条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从11到nn的连续正整数。

现在有mm个玩家,第ii个玩家的起点为 S_iS?i??,终点为 T_iT?i?? 。每天打卡任务开始时,所有玩家在第00秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)

小C想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点jj的观察员会选择在第W_jW?j??秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第W_jW?j??秒也理到达了结点 jj 。 小C想知道每个观察员会观察到多少人?

注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点jj作为终点的玩家: 若他在第W_jW?j??秒重到达终点,则在结点jj的观察员不能观察到该玩家;若他正好在第W_jW?j??秒到达终点,则在结点jj的观察员可以观察到这个玩家。

输入输出格式

输入格式：

 

第一行有两个整数nn和mm 。其中nn代表树的结点数量, 同时也是观察员的数量, mm代表玩家的数量。

接下来 n- 1n−1行每行两个整数uu和 vv,表示结点 uu到结点 vv有一条边。

接下来一行 nn个整数,其中第jj个整数为W_jW?j?? , 表示结点jj出现观察员的时间。

接下来 mm行,每行两个整数S_iS?i??,和T_iT?i??,表示一个玩家的起点和终点。

对于所有的数据,保证1leq S_i,T_ileq n, 0leq W_jleq n1≤S?i??,T?i??≤n,0≤W?j??≤n 。

 

输出格式：

 

输出1行 nn个整数,第jj个整数表示结点jj的观察员可以观察到多少人。

 

输入输出样例

输入样例#1：

6 3
2 3
1 2 
1 4 
4 5 
4 6 
0 2 5 1 2 3 
1 5 
1 3 
2 6 

输出样例#1：

2 0 0 1 1 1 

输入样例#2：

5 3 
1 2 
2 3 
2 4 
1 5 
0 1 0 3 0 
3 1 
1 4
5 5 

输出样例#2：

1 2 1 0 1 

说明

【样例1说明】

对于1号点，W_i=0W?i??=0，故只有起点为1号点的玩家才会被观察到，所以玩家1和玩家2被观察到，共有2人被观察到。

对于2号点，没有玩家在第2秒时在此结点，共0人被观察到。

对于3号点，没有玩家在第5秒时在此结点，共0人被观察到。

对于4号点，玩家1被观察到，共1人被观察到。

对于5号点，玩家1被观察到，共1人被观察到。

对于6号点，玩家3被观察到，共1人被观察到。

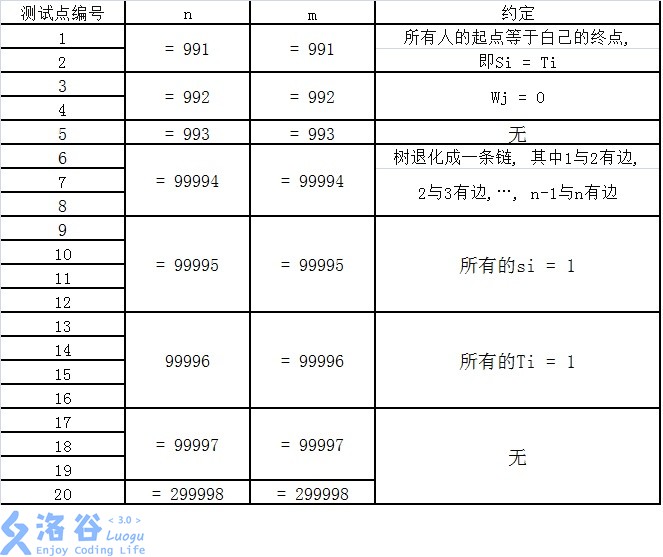
【子任务】

每个测试点的数据规模及特点如下表所示。 提示: 数据范围的个位上的数字可以帮助判断是哪一种数据类型。

题目大意：n个节点的树，每个点都有观察员，观察员观察的时间是w[i],有m个玩家，从u跑到v，1s跑一条边，

只有跑到某个节点上的时间与观察员观察的时间相等时，才能被观察到，问每个观察员能观察到几个人。

题解：

步骤分：

（1）25分 前5个测试点，数据较小，搜索可过，前4个判断一下也能过。

  代码：

/*
前5个测试点暴力求解。dfs
*/
#include<cstdio>
#define maxn 300005
using namespace std;
int n,m,sumedge,u,v,ok;
int w[maxn],head[maxn],a[1002][1002];

struct Edge{
    int x,y,nxt;
    Edge(int x=0,int y=0,int nxt=0):
        x(x),y(y),nxt(nxt){}
}edge[maxn<<1];

void add(int x,int y){
    edge[++sumedge]=Edge(x,y,head[x]);
    head[x]=sumedge;
}

void run(int now,int ed,int tim,int fa){
    if(now==ed){ok=true;a[now][tim]++;return;}
    if(ok)return;//一旦找到路径 dfs的分支都会被cnt掉 
    for(int i=head[now];i;i=edge[i].nxt){
        int v=edge[i].y;
        if(v==fa)continue;
        run(v,ed,tim+1,now);
    }
    if(ok)a[now][tim]++;
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<n;i++){scanf("%d%d",&u,&v);add(u,v);add(v,u);}
    for(int i=1;i<=n;i++)scanf("%d",&w[i]);
    for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);ok=false;run(u,v,0,0);}
    for(int i=1;i<=n;i++){printf("%d ",a[i][w[i]]);}
    return 0;
}

（2）40分 6--8个测试点 此时树成为了一条链，节点的编号为节点的深度。

设某个玩家的起点为S终点为T，假设S<T。

 那么对于S--T路径上一点i，如果能观察到该玩家，那么满足i-S=w[i]。

那么S=i-w[i]。由此可以看出，等式右边都为i的信息，那么某个点i观察到的人

的起点是确定的，i-w[i]。综上，当S>T时，S=i+w[i]。所以，i点只能观察到

起点为i+w[i]和 i-w[i],我们只需判断一下起点为i+w[i]和i-w[i]出发的玩家是否经过

i，用vector存，然后枚举一下。

代码

/*成为一条链时，一开始vec的size从1开始了嘤嘤嘤蠢哭=n=*/ 
#include<cstdio>
#include<vector>
#define maxn 300005
using namespace std;
vector<int>vec[maxn];
struct PE{int u,v;}p[maxn];
int n,m,u,v,w[maxn],ans[maxn];
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<n;i++)scanf("%d%d",&u,&v);
    for(int i=1;i<=n;i++)scanf("%d",&w[i]);
    for(int i=1;i<=m;i++){scanf("%d%d",&p[i].u,&p[i].v);vec[p[i].u].push_back(i);}
    for(int i=1;i<=n;i++){
        if(i-w[i]>=1){
            for(int j=0;j<vec[i-w[i]].size();j++){
                if(p[vec[i-w[i]][j]].v>=i)ans[i]++;
            }
        }
        if(i+w[i]<=n){
            for(int j=0;j<vec[i+w[i]].size();j++){
                if(p[vec[i+w[i]][j]].v<=i)ans[i]++;
            }
        }
    }
    for(int i=1;i<=n;i++)printf("%d ",ans[i]);
    return 0;
} 

(3）60分。此时的每个玩家的起点都为1，考虑点i能够观察到玩家的可能性为deep[i]=w[i]，

那么该点能够观测到的玩家个数为终点在其子树的玩家个数，dfs处理就可以了。

代码

/*起点为1时*/
#include<cstdio>
#define maxn 300005
using namespace std;

int n,m,u,v,sumedge;
int head[maxn],ans[maxn],w[maxn],dad[maxn],deep[maxn],sum[maxn];

struct Edge{
    int x,y,nxt;
    Edge(int x=0,int y=0,int nxt=0):
        x(x),y(y),nxt(nxt){}
}edge[maxn<<1];

void add(int x,int y){
    edge[++sumedge]=Edge(x,y,head[x]);
    head[x]=sumedge;
}

void dfs(int x){
    for(int i=head[x];i;i=edge[i].nxt){
        int v=edge[i].y;
        if(v==dad[x])continue;
        dad[v]=x;deep[v]=deep[x]+1;
        dfs(v);
        sum[x]+=sum[v];
    }
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<n;i++){scanf("%d%d",&u,&v);add(u,v);add(v,u);}
    for(int i=1;i<=n;i++)scanf("%d",&w[i]);
    for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);sum[v]++;}
    dfs(1);
    for(int i=1;i<=n;i++){if(deep[i]==w[i])ans[i]+=sum[i];printf("%d ",ans[i]);}
    return 0;
}

咳咳 正解：不写了。鸽了。