数据结构-----栈
Posted alimayun
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构-----栈相关的知识,希望对你有一定的参考价值。
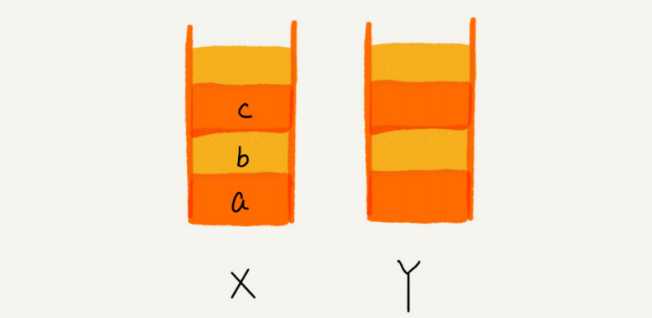
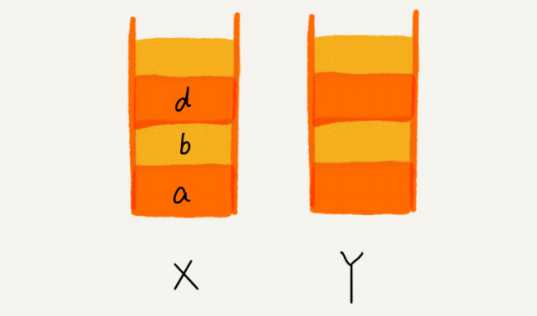
浏览器的前进、后退功能,我想你肯定很熟悉吧?当你依次访问完一串页面 a-b-c 之后,点击浏览器的后退按钮,就可以查看之前浏览过的页面 b 和 a。当你后退到页面 a,点击前进按钮,就可以重新查看页面 b 和 c。但是,如果你后退到页面 b 后,点击了新
的页面 d,那就无法再通过前进、后退功能查看页面 c 了。假设你是 Chrome 浏览器的开发工程师,你会如何实现这个功能呢?这就要用到我们今天要讲的“栈”这种数据结构。
如何理解“栈”?
如何实现一个“栈”?
栈的主要操作其实只有两个,一个入栈,一个出栈。我们可以使用数组或链表来实现栈结构。用数组实现的栈,我们叫作顺序栈,用链表实现的栈,我们叫作链式栈。
代码示例:
// 基于数组实现的顺序栈 public class ArrayStack { private String[] items; // 数组 private int count; // 栈中元素个数 private int n; // 栈的大小 // 初始化数组,申请一个大小为 n 的数组空间 public ArrayStack(int n) { this.items = new String[n]; this.n = n; this.count = 0; } // 入栈操作 public boolean push(String item) { // 数组空间不够了,直接返回 false,入栈失败。 if(count == n) return false; // 将 item 放到下标为 count 的位置,并且 count 加一 items[count] = item; ++count; return true; } // 出栈操作 public String pop() { // 栈为空,则直接返回 null if (count == 0) return null; // 返回下标为 count-1 的数组元素,并且栈中元素个数 count 减一 String tmp = items[count-1]; --count; return tmp; } }
不管是顺序栈还是链式栈,空间复杂度是 O(1)。不管是顺序栈还是链式栈,入栈、出栈只涉及栈顶个别数据的操作,所以时间复杂度都是 O(1)。
不过上面这种数组实现的栈结构不支持动态扩容。链表实现的栈结构虽然可以动态扩容,但是每个结点都需要保存next指针,会增加内存的消耗,
实现动态扩容的栈-----数组结构
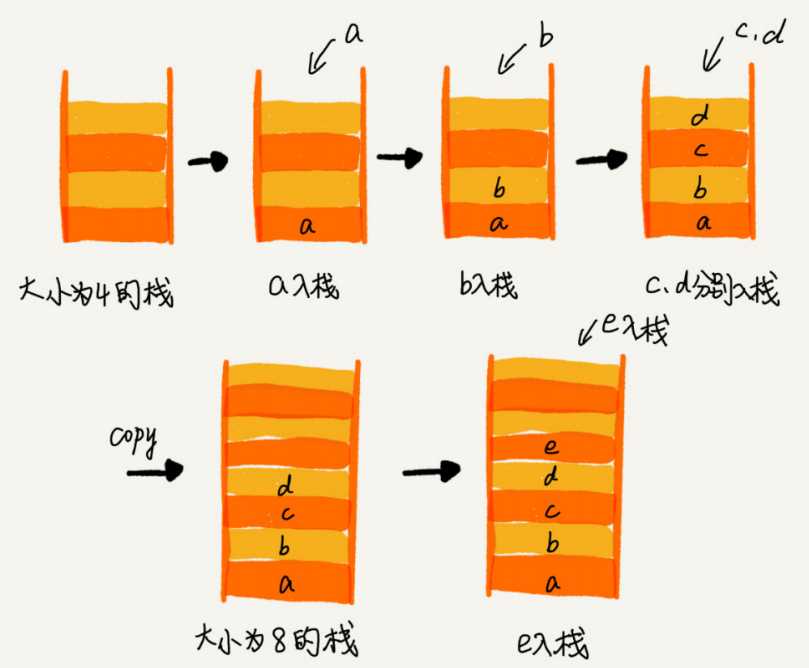
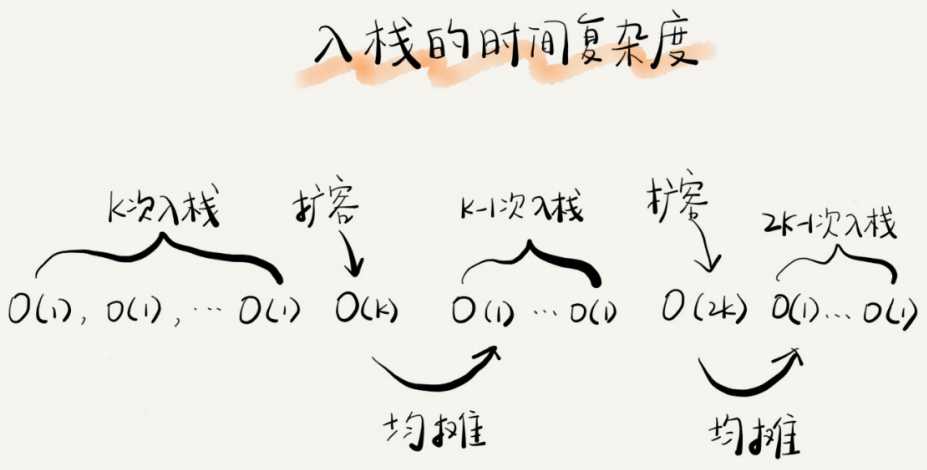
为了分析的方便,我们需要事先做一些假设和定义:栈空间不够时,我们重新申请一个是原来大小两倍的数组;为了简化分析,假设只有入栈操作没有出栈操作;定义不涉及内存搬移的入栈操作为 simple-push 操作,时间复杂度为 O(1)。如果当前栈大小为
K,并且已满,当再有新的数据要入栈时,就需要重新申请 2 倍大小的内存,并且做 K 个数据的搬移操作,然后再入栈。但是,接下来的 K-1 次入栈操作,我们都不需要再重新申请内存和搬移数据,所以这 K-1 次入栈操作都只需要一个 simple-push操作就可以
完成。
栈在函数调用中的应用
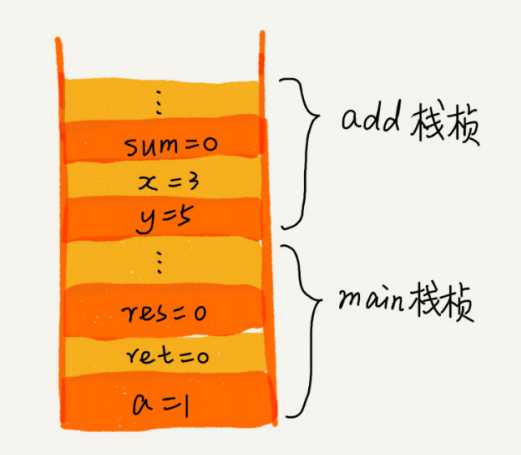
栈作为一个比较基础的数据结构,应用场景还是蛮多的。其中,比较经典的一个应用场景就是函数调用栈。我们知道,操作系统给每个线程分配了一块独立的内存空间,这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数,就会
将临时变量作为一个栈帧入栈,当被调用函数执行完成,返回之后,将这个函数对应的栈帧出栈。
int main() { int a = 1; int ret = 0; int res = 0; ret = add(3, 5); res = a + ret; printf("%d", res); reuturn 0; } int add(int x, int y) { int sum = 0; sum = x + y; return sum; }
从代码中我们可以看出,main() 函数调用了 add() 函数,获取计算结果,并且与临时变量a 相加,最后打印 res 的值。
栈在表达式求值中的应用
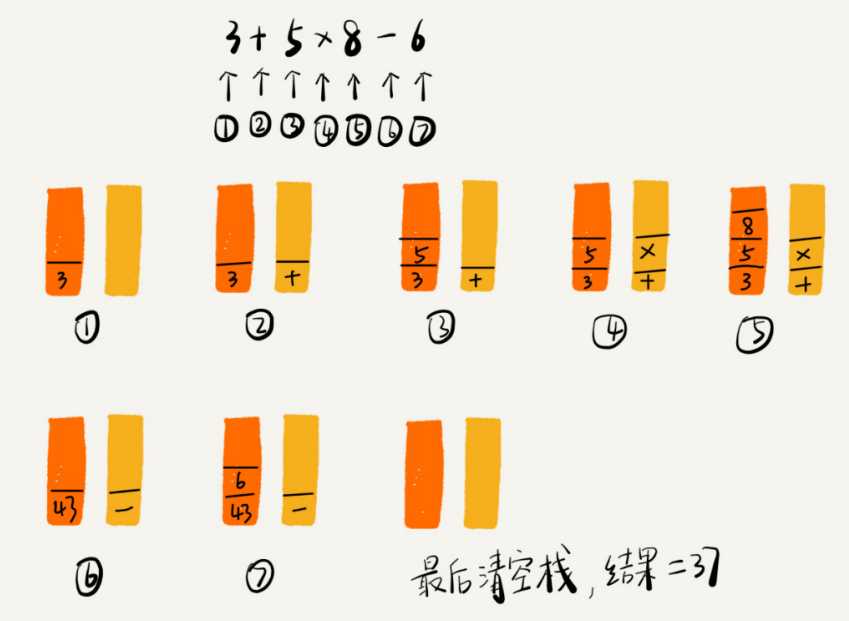
我们再来看栈的另一个常见的应用场景,编译器如何利用栈来实现表达式求值。实际上,编译器就是通过两个栈来实现的。其中一个保存操作数的栈,另一个是保存运算符的栈。我们从左向右遍历表达式,当遇到数字,我们就直接压入操作数栈;当遇到运算
符,就与运算符栈的栈顶元素进行比较。如果比运算符栈顶元素的优先级高,就将当前运算符压入栈;如果比运算符栈顶元素的优先级低或者相同,从运算符栈中取栈顶运算符,从操作数栈的栈顶取 2 个操作数,然后进行计算,再把计算完的结果压入操作数
栈,继续比较。
例如3+5*8-6,如图所示:
如何实现浏览器前进后退的功能?
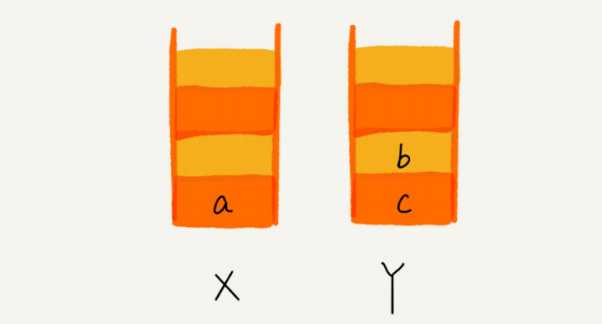
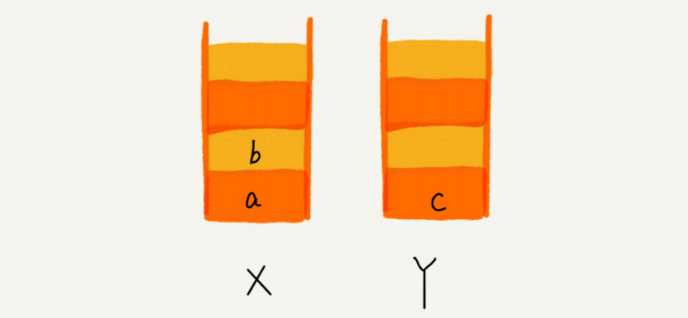
以上是关于数据结构-----栈的主要内容,如果未能解决你的问题,请参考以下文章