Counting Sort and Radix Sort

Posted 2020-12-12 eimadrigal

Counting Sort

计数排序适用于数据量很大，但是数据类别很少的情况，可以做到线性时间。
举例来看：如果有100万个字符串，但只有cat, dog, person三种类型，采用基于比较的排序方式，可以做到(NlogN)，计数排序采用了一种完全不同的思想：

• 新建一个counts[3]，记录每种类型数据的出现次数；
• 遍历待排序数组，完成count[]的统计，并创建一个结果数组sorted[]：
  
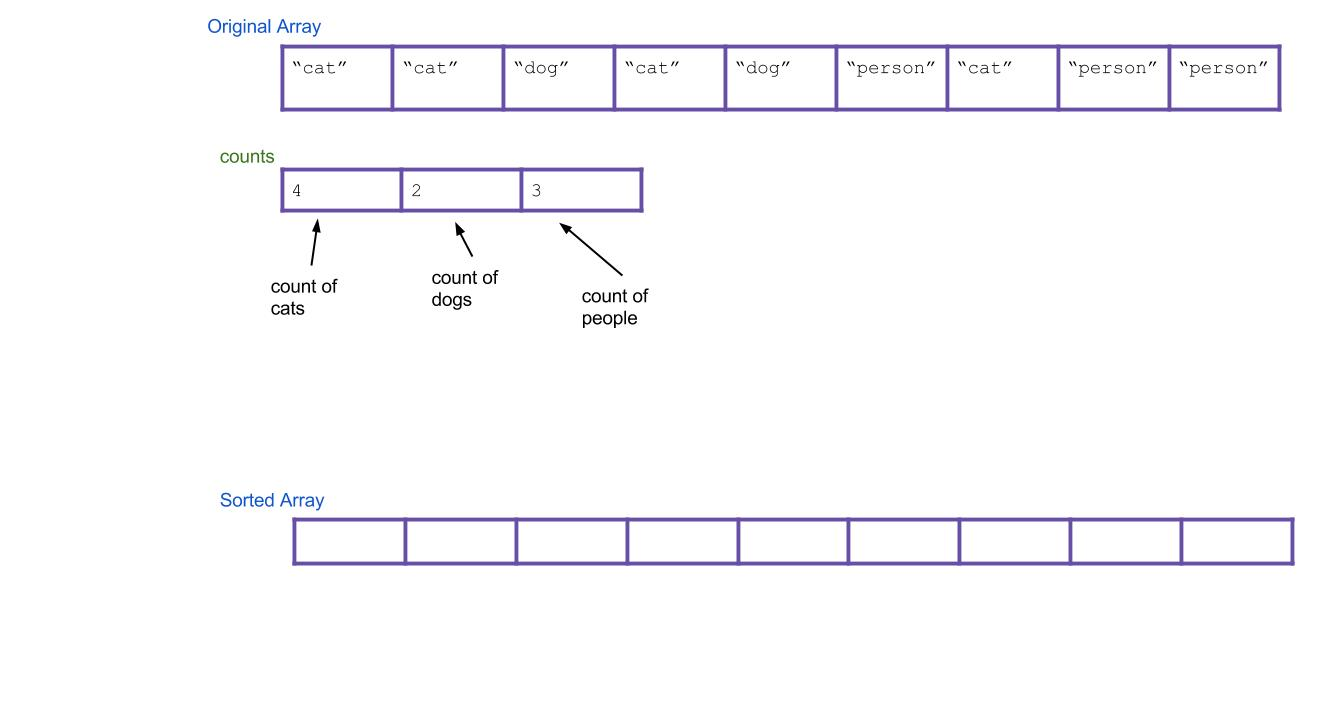
• 基于count[]，我们完全可以知道第一个cat应该放置在0，第一个dog应该放置在count[0]=4处，第一个person应该放置在count[0]+count[1]=6处，为了更加清晰，创建一个starts[3]表示每类数据中的第一个的起始位置：
  
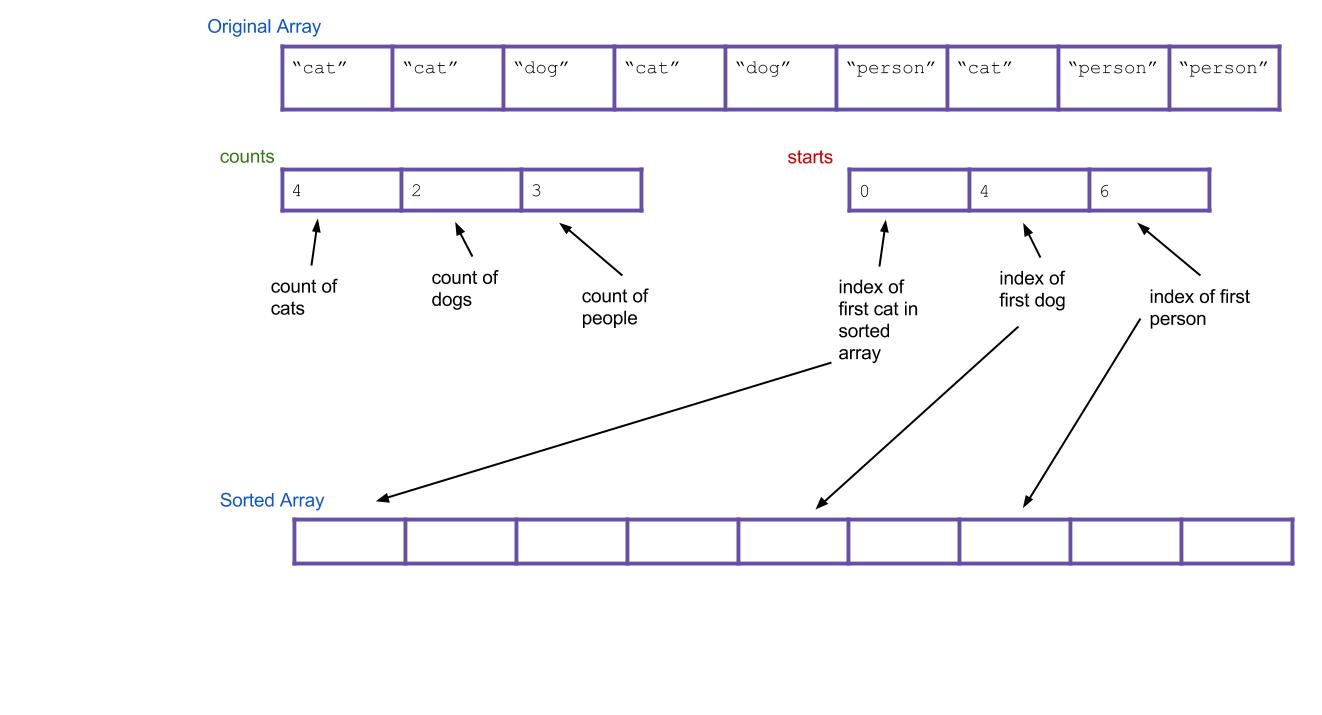
• 接着第二次遍历待排序数组，遇到第一个cat，我们知道它应该放在sorted[starts[0]]；第一个dog应该放在sorted[starts[1]]，第二个dog应该放在sorted[starts[1]+1]。或者可以这样做：每当放置完一个dog，就++starts[1]，这样下一次的dog还是会放在sorted[starts[1]]，最终结果：
  

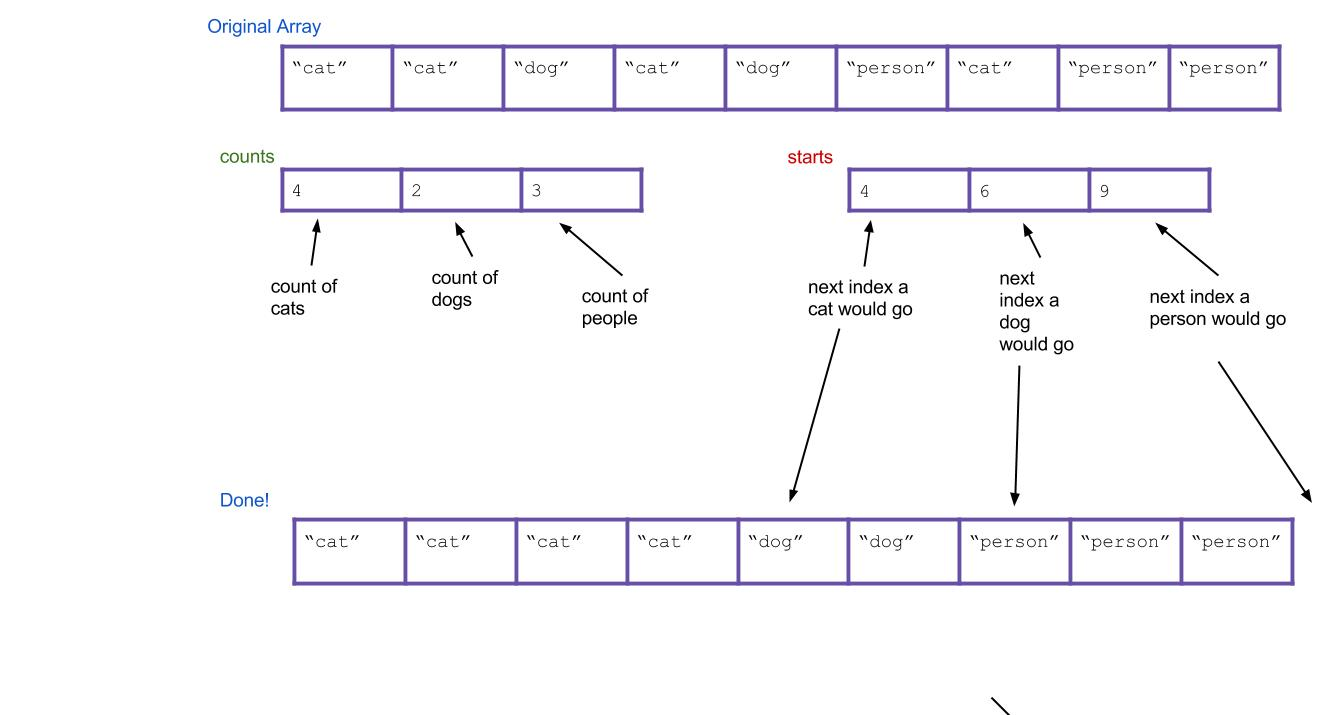
对于字符串排序，我们需要规定counts[]中每个下标对应哪种类型。如果对于非负整数，我们可以用counts[i]表示i的出现次数，接着遍历counts[]，将整数i放置counts[i]次；如果有负数，可以找到最小值min和最大值max，平移到0~max-min即可。

Radix Sort

计数排序的前提就是需要知道待排序数组的内容/范围，那么如果范围很大，空间上是无法忍受的，由此来看更加general的基数排序：如果给定某种基（二进制2/十进制10/小写字母26）下的待排序数据，基数排序会逐位处理。基数排序有两种方式：

1. LSD(Least Significant Digit)
   首先按照最右边一位排序，依次处理左边的每一位：
   356, 112, 904, 294, 209, 820, 394, 810；
   820, 810, 112, 904, 294, 394, 356, 209；
   904, 209, 810, 112, 820, 356, 294, 394；
   112, 209, 294, 356, 394, 810, 820, 904。
   由于对第二位排序不能改变第一位排序的结果，所以要求按位排序算法必须是稳定的。
2. MSD(Most Significant Digit)
   从左到右处理，MSD需要用到桶：
   [112], [294, 209], [356, 394], [820, 810], [904]；
   对于每个桶采用类似的方法直到最后一位，以[294, 209]为例，接着处理第二位：[209], [294]。
   最后收集每个桶中的元素即可。

Reference

具体实现不知道LSD哪里实现的有问题，提交AutoGrader总是超时。
lab 13 Radix Sorts