泊松分布

Posted 2020-12-12 gloria-zhang

泊松分布泊松分布适用于在随机时间和空间上发生事件的情况，其中，我们只关注事件发生的次数。
当以下假设有效时，则称为泊松分布：
* 任何一个成功的事件都不应该影响另一个成功的事件。
* 在短时间内成功的概率必须等于在更长的时间内成功的概率。
* 时间间隔很小时，成功的概率趋近于零。

??是事件发生的频率，也就是单位时间（或单位面积内随机事件的平均发生率），t是时间间隔，X是该时间间隔内的事件数。X称为泊松随机变量，X的概率分布称为泊松分布。??表示长度为t的时间间隔中的平均事件数，那么??=??*t。

通俗定义：假定一个事件在一段时间内随机发生，且符合以下条件：
* 将该时间段无限分隔成若干个小的时间段，在这个接近于零的小时间段内，该事件发生一次的概率与这个极小时间段的长度成正比。
* 在每一个极小时间段内，该事件发生两次及两次以上的概率恒等于零。
* 该事件在不同的小时间段内，发生与否相互独立。
公式：
$$fleft( x｜lambda ight) =dfrac {lambda ^{x}e^{-lambda }}{x!}$$

---

 

泊松分布相关代码

#导入库
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
from collections import Counter

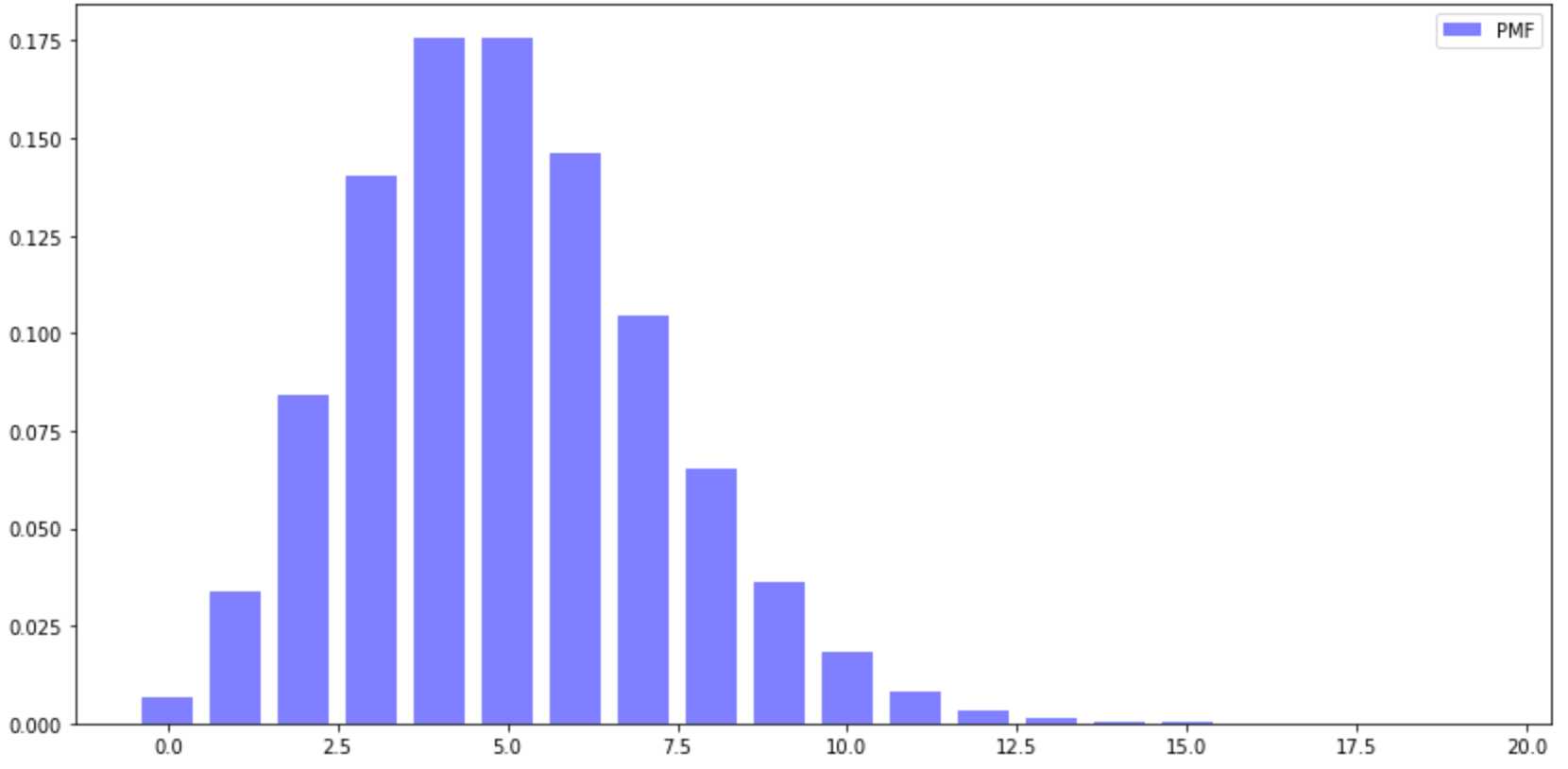
PMF

#PMF
plt.figure(figsize=(14,7))

x=np.arange(20)
y=stats.poisson.pmf(x,mu=5)

plt.figure(figsize=(14,7))
plt.bar(x,
        y,
        width=0.75,
        alpha=0.5,
        color=‘b‘,
        label=‘PMF‘,
       )

plt.legend()
plt.show()

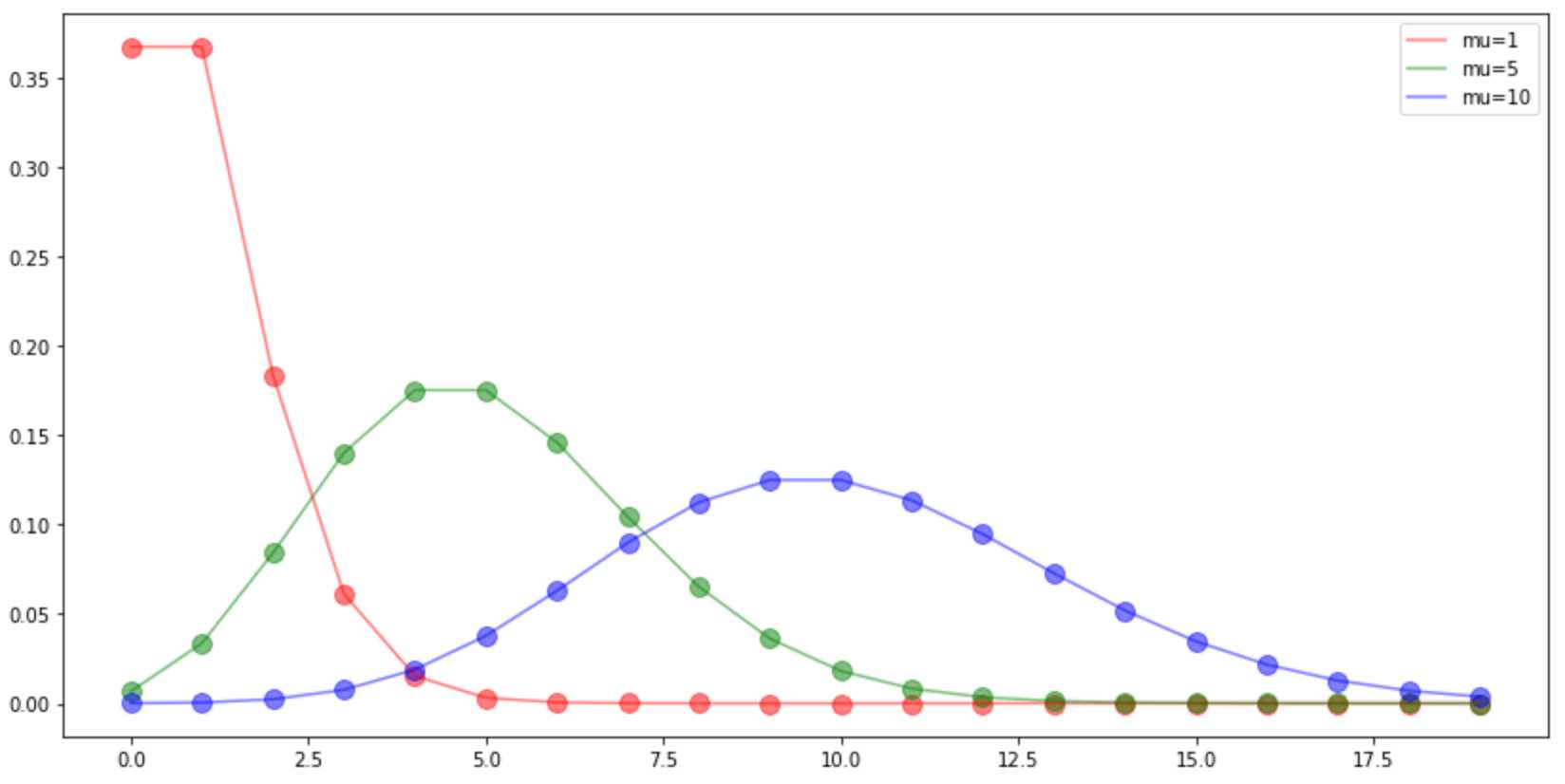
 ??值的影响

#??值不同
plt.figure(figsize=(14,7))

x=np.arange(20)
y1=stats.poisson.pmf(x,mu=1)
y2=stats.poisson.pmf(x,mu=5)
y3=stats.poisson.pmf(x,mu=10)

plt.scatter(x,
            y1,
            alpha=0.5,
            color=‘r‘,
            s=100,
           )

plt.plot(x,
         y1,
         alpha=0.5,
         color=‘r‘,
         label=‘mu=1‘,
        )

plt.scatter(x,
            y2,
            alpha=0.5,
            color=‘g‘,
            s=100,
           )

plt.plot(x,
         y2,
         alpha=0.5,
         color=‘g‘,
         label=‘mu=5‘,
        )

plt.scatter(x,
            y3,
            alpha=0.5,
            color=‘b‘,
            s=100,
           )

plt.plot(x,
         y3,
         alpha=0.5,
         color=‘b‘,
         label=‘mu=10‘,
        )

plt.legend()
plt.show()

 

随机样本

#随机样本
np.random.seed(0)
print(stats.poisson.rvs(mu=10),end=‘

‘)
print(stats.poisson.rvs(mu=10,size=10),end=‘

‘)

 

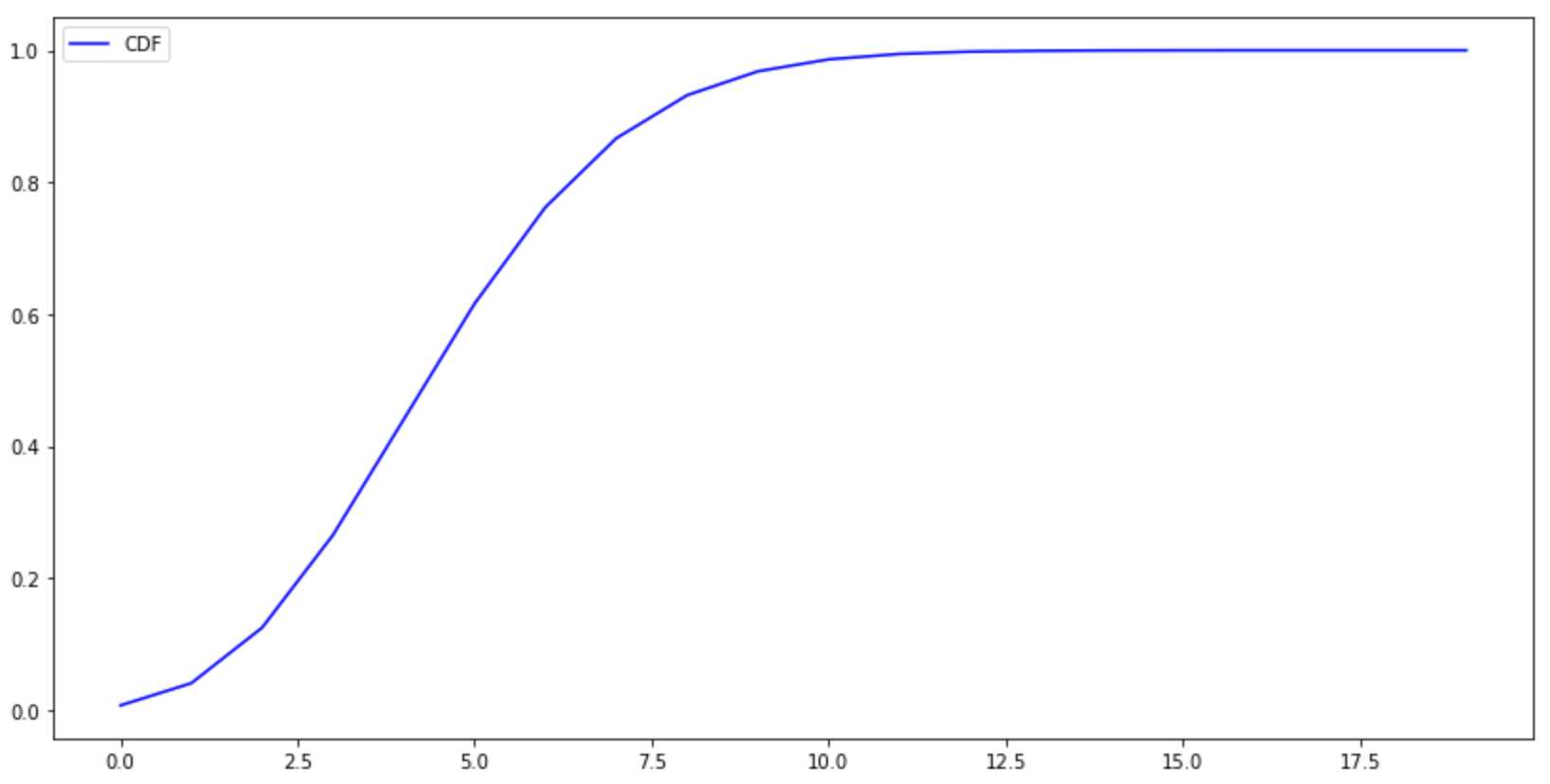
CDF

#CDF
x=np.arange(20)
y=stats.poisson.cdf(x,mu=5)

plt.figure(figsize=(14,7))
plt.plot(x,
         y,
         color=‘b‘,
         label=‘CDF‘
        )

plt.legend()
plt.show()

 

区间概率

print(‘P(X<3)={}‘.format(stats.poisson.cdf(k=3,mu=5)))
print(‘P(2<X<=8)={}‘.format(stats.poisson.cdf(k=8,mu=5)-stats.poisson.cdf(k=2,mu=5)))