书中第介绍了有根树,简单介绍了二叉树和分支数目无限制的有根树的存储结构,而没有关于二叉树的遍历过程。为此对二叉树做个简单的总结,介绍一下二叉树基本概念、性质、二叉树的存储结构和遍历过程,主要包括先根遍历、中根遍历、后根遍历和层次遍历。
1、二叉树的定义
二叉树(Binary Tree)是一种特殊的树型结构,每个节点至多有两棵子树,且二叉树的子树有左右之分,次序不能颠倒。
由定义可知,二叉树中不存在度(结点拥有的子树数目)大于2的节点。二叉树形状如下下图所示: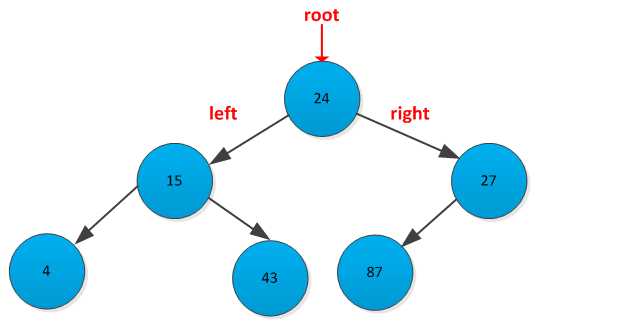
2、二叉树的性质
(1)在二叉树中的第i层上至多有2^(i-1)个结点(i>=1)。备注:^表示此方
(2)深度为k的二叉树至多有2^k-1个节点(k>=1)。
(3)对任何一棵二叉树T,如果其终端结点数目为n0,度为2的节点数目为n2,则n0=n2+1。
满二叉树:深度为k且具有2^k-1个结点的二叉树。即满二叉树中的每一层上的结点数都是最大的结点数。
完全二叉树:深度为k具有n个结点的二叉树,当且仅当每一个结点与深度为k的满二叉树中的编号从1至n的结点一一对应。
可以得到一般结论:满二叉树和完全二叉树是两种特殊形态的二叉树,满二叉树肯定是完全二叉树,但完全二叉树不不一定是满二叉树。
举例如下图是所示:
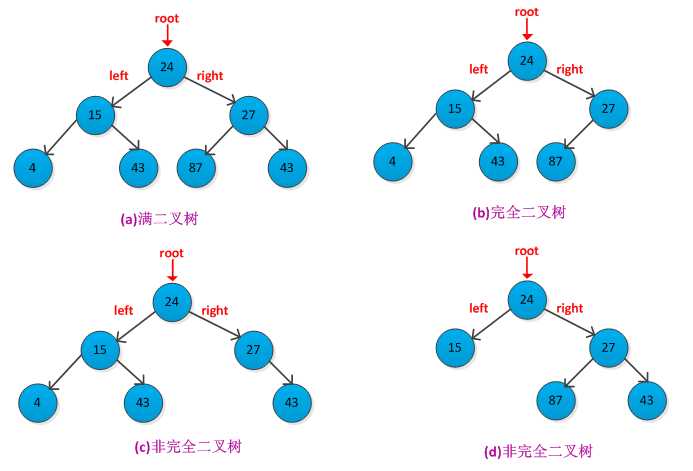
(4)具有n个节点的完全二叉树的深度为log2n + 1。
3、二叉树的存储结构
可以采用顺序存储数组和链式存储二叉链表两种方法来存储二叉树。经常使用的二叉链表方法,因为其非常灵活,方便二叉树的操作。二叉树的二叉链表存储结构如下所示:
1 typedef struct binary_tree_node
2 {
3 int elem;
4 struct binary_tree_node *left;
5 struct binary_tree_node *right;
6 }binary_tree_node,*binary_tree;
举例说明二叉链表存储过程,如下图所示:
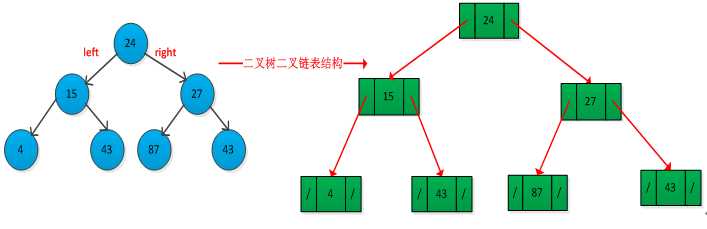
从图中可以看出:在还有n个结点的二叉链表中有n+1个空链域。
4、遍历二叉树
遍历二叉树是按照指定的路径方式访问书中每个结点一次,且仅访问一次。由二叉树的定义,我们知道二叉数是由根结点、左子树和右子树三部分构成的。通常遍历二叉树是从左向右进行,因此可以得到如下最基本的三种遍历方法:
(1)先根遍历(先序遍历):如果二叉树为空,进行空操作;否则,先访问根节点,然后先根遍历左子树,最后先根遍历右子树。采用递归形式实现代码如下:
1 void preorder_traverse_recursive(binary_tree root)
2 {
3 if(NULL != root)
4 {
5 printf("%d ",root->elem);
6 preorder_traverse_recursive(root->left);
7 preorder_traverse_recursive(root->right);
8 }
9 }
具体过程如下图所示:
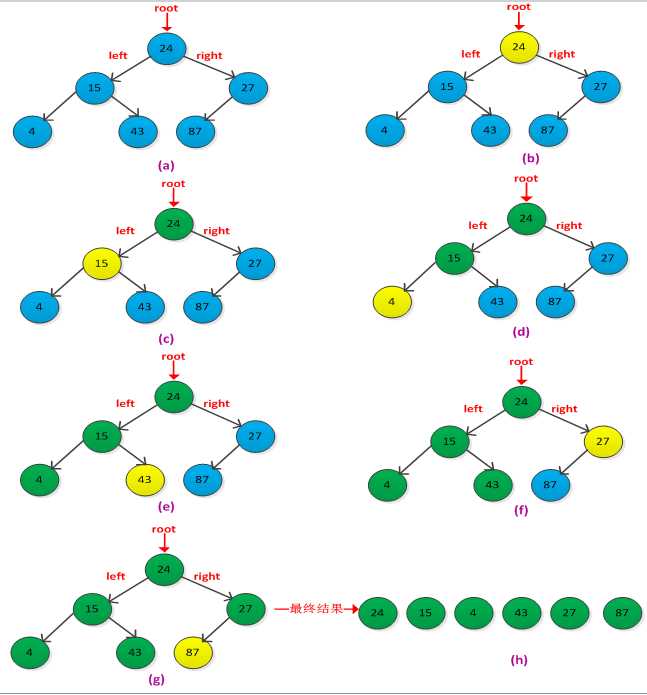
(2)中根遍历(中序遍历):如果二叉树为空,进行空操作;否则,先中根遍历左子树,然后访问根结点,最后中根遍历右子树。递归过程实现代码如下:
1 void inorder_traverse_recursive(binary_tree root)
2 {
3 if(NULL != root)
4 {
5 inorder_traverse_recursive(root->left);
6 printf("%d ",root->elem);
7 inorder_traverse_recursive(root->right);
8 }
9 }
具体过程如下图所示:
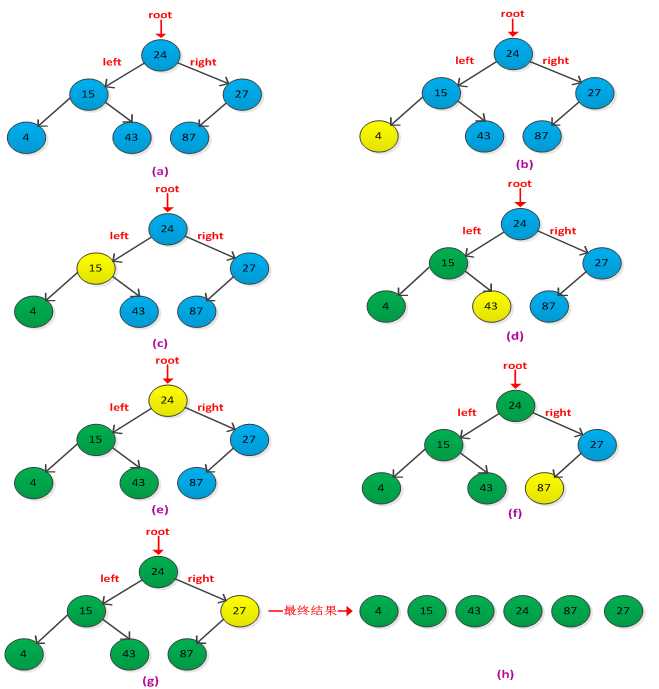
(3)后根遍历(后序遍历):如果二叉树为空,进行空操作;否则,先后根遍历左子树,然后后根遍历右子树,最后访问根结点。递归实现代码如下:
1 void postorder_traverse_recursive(binary_tree root)
2 {
3 if(NULL != root)
4 {
5 postorder_traverse_recursive(root->left);
6 postorder_traverse_recursive(root->right);
7 printf("%d ",root->elem);
8 }
9 }
具体过程如下图所示:
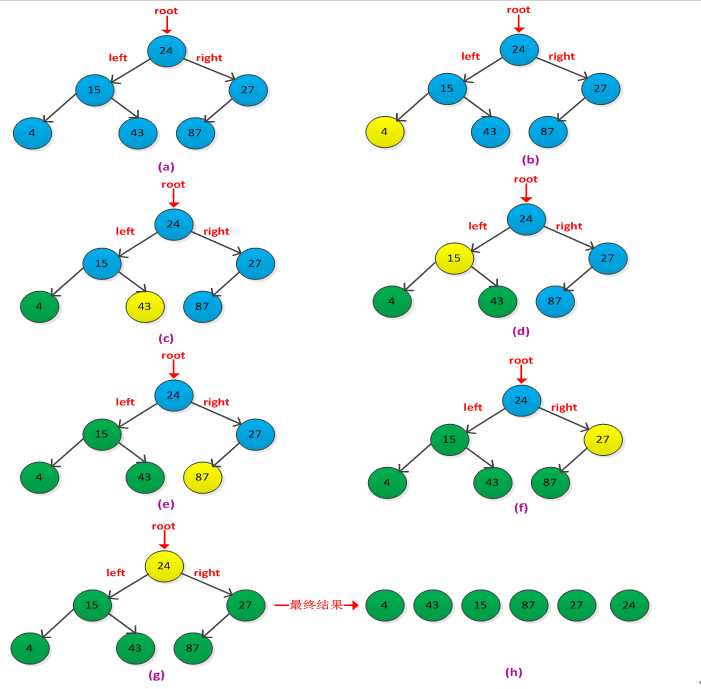
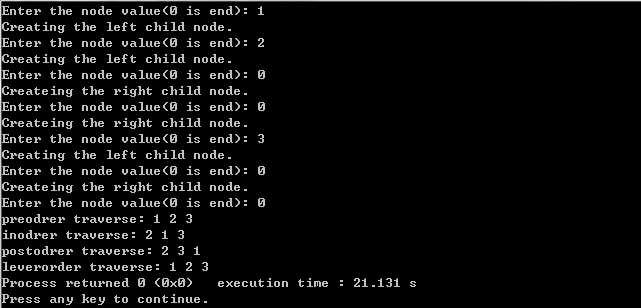
写一个完整的程序练习二叉树的三种遍历,采用递归形式创建二叉树,然后以递归的形式遍历二叉树,后面会接着讨论如何使用非递归形式实现这三种遍历,程序采用C语言实现,完整程序如下:
 View Code
View Code程序测试结果如下:
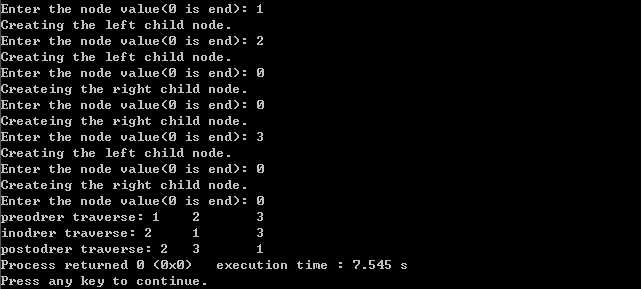
现在来讨论一下如何采用非递归实现这以上三种遍历。将递归形式转换为非递归形式,引入了额外的辅助结构栈。另外在讨论一次二叉树的层次遍历,可以借助队列进行实现。具体讨论如下:
(1)先根遍历非递归实现
先根遍历要求顺序是根左右,可以借助栈s来实现。先将根root入栈,然后循环判断s是否为空,非空则将结点出栈,记为节点p,然后依次先将结点p的右子树结点入栈,然后将结点p的左子树结点入栈,循环操作直到栈中所有元素都出栈为止,出栈顺序即是先根遍历的结果。采用C++中模板库stack实现先根遍历如下:
1 void preorder_traverse(binary_tree root)
2 {
3 if(NULL != root)
4 {
5 stack<binary_tree_node*> s;
6 binary_tree_node *ptmpnode;
7 s.push(root);
8 while(!s.empty())
9 {
10 ptmpnode = s.top();
11 cout<<ptmpnode->elem<<" ";
12 s.pop();
13 if(NULL != ptmpnode->right)
14 s.push(ptmpnode->right);
15 if(NULL != ptmpnode->left)
16 s.push(ptmpnode->left);
17
18 }
19 }
20 }
(2)中根遍历非递归实现
中根遍历要求顺序是左根右,借助栈s实现。先将根root入栈,接着从根root开始查找最左的子孩子结点直到为空为止,然后将空节点出栈,再将左子树节点出栈遍历,然后判断该左子树的右子树节点入栈。循环此过程,直到栈为空为止。此时需要注意的是入栈过程中空结点也入栈了,用以判断左孩子是否结束和左孩子是否有右孩子结点。采用C++中模板库stack实现先根遍历如下:
1 void inorder_traverse(binary_tree root)
2 {
3 if(NULL != root)
4 {
5 stack<binary_tree_node*> s;
6 binary_tree_node *ptmpnode;
7 s.push(root);
8 while(!s.empty())
9 {
10 ptmpnode = s.top();
11 while(NULL != ptmpnode)
12 {
13 s.push(ptmpnode->left);
14 ptmpnode = s.top();
15 }
16 s.pop();//空结点出栈
17 if(!s.empty())
18 {
19 ptmpnode = s.top();
20 cout<<ptmpnode->elem<<" ";
21 s.pop();
22 //右子树结点如栈
23 s.push(ptmpnode->right);
24 }
25 }
26 }
27 }
另外一种简洁的实现方法如下:
1 void inorder_traverse_two(binary_tree root)
2 {
3 if(NULL != root)
4 {
5 stack<binary_tree_node*> s;
6 binary_tree_node *ptmpnode;
7 ptmpnode = root;
8 while(NULL != ptmpnode || !s.empty())
9 {
10 //将左子树结点入栈
11 if(NULL != ptmpnode)
12 {
13 s.push(ptmpnode);
14 ptmpnode = ptmpnode->left;
15 }
16 else
17 {
18 //出栈遍历
19 ptmpnode = s.top();
20 s.pop();
21 cout<<ptmpnode->elem<<" ";
22 //右子树结点
23 ptmpnode = ptmpnode->right;
24 }
25 }
26 }
27 }
(3)后根遍历递归实现
后根遍历要求访问顺序是左右根,采用辅助栈实现时,需要一个标记,判断结点是否访问了,因为右子树是通过跟结点的信息得到的。实现过程是先将根结点及其左子树入栈,并初始标记为0,表示没有访问,然后通过判断栈是否为空和标记的值是否为1来判断是否访问元素。
参考:http://www.cnblogs.com/hicjiajia/archive/2010/08/27/1810055.html
采用C++模板库stack具体实现程序如下:
1 void postorder_traverse(binary_tree root)
2 {
3 if(NULL != root)
4 {
5 stack<binary_tree_node*> s;
6 binary_tree_node *ptmpnode;
7 int flags[100];
8 ptmpnode = root;
9 while(NULL != ptmpnode || !s.empty())
10 {
11 //将结点左子树结点入栈
12 while(NULL != ptmpnode)
13 {
14 s.push(ptmpnode);
15 flags[s.size()] = 0; //标记未访问
16 ptmpnode=ptmpnode->left;
17 }
18 //输出访问的结点
19 while(!s.empty() && flags[s.size()] == 1)
20 {
21 ptmpnode = s.top();
22 s.pop();
23 cout<<ptmpnode->elem<<" ";
24 }
25 //从右子树开始遍历
26 if(!s.empty())
27 {
28 ptmpnode = s.top();
29 flags[s.size()] = 1; //登记访问了
30 ptmpnode = ptmpnode->right;
31 }
32 else
33 break;
34 }
35 }
36 }
(4)层次遍历实现
层次遍历要求从根向下、从左向右进行访问,可以采用队列实现。先将根入队,然后队列进程出队操作访问结点p,再将结点p的左子树和右子树结点入队,循环执行此过程直到队列为空。出队顺序即是层次遍历结果。采用C++的模板库queue实现如下:
1 void levelorder_traverse(binary_tree root)
2 {
3 if(NULL != root)
4 {
5 queue<binary_tree_node*> q;
6 binary_tree_node *ptmpnode;
7 q.push(root);
8 while(!q.empty())
9 {
10 ptmpnode = q.front();
11 q.pop();
12 cout<<ptmpnode->elem<<" ";
13 if(NULL != ptmpnode->left)
14 q.push(ptmpnode->left);
15 if(NULL != ptmpnode->right)
16 q.push(ptmpnode->right);
17 }
18 }
19 }
综合上面的分析过程写个完整的程序测试二叉树遍历的非递归实现,采用C++语言,借助stack和queue实现,完整程序如下所示:
 View Code
View Code程序测试结果如下: