线性变换
Posted pluslius
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性变换相关的知识,希望对你有一定的参考价值。
线性变换
2D旋转
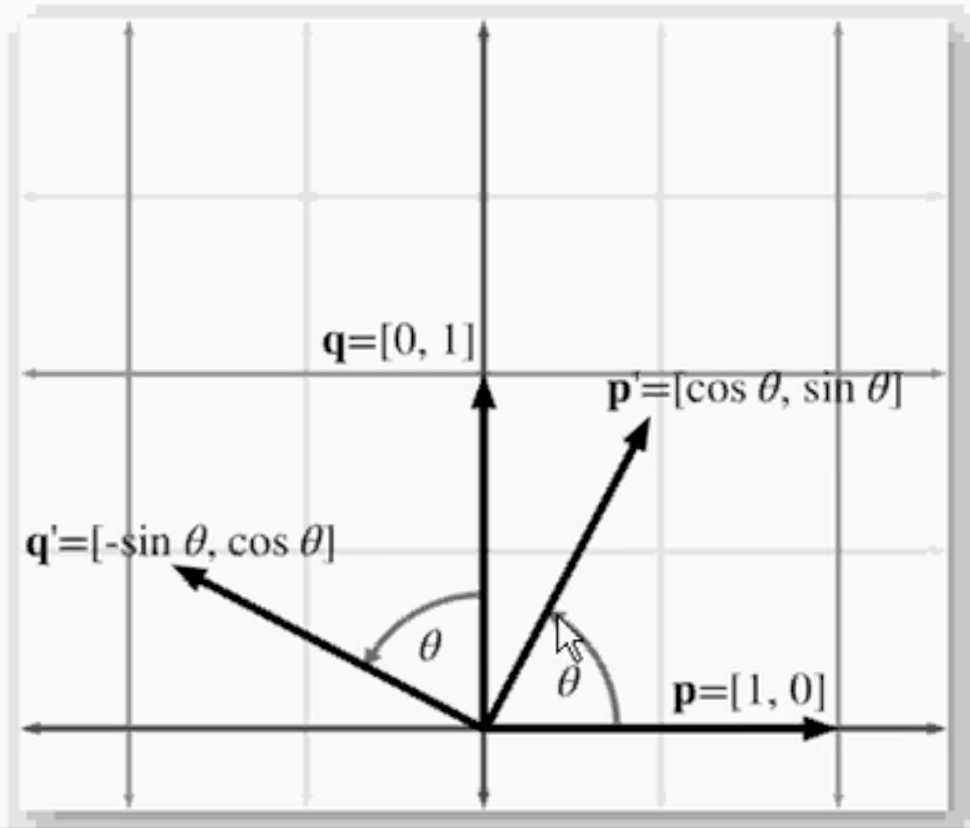
aM = b
2D旋转矩阵
[left[
egin{matrix}
x \\
y
end{matrix}
ight] imes
left[
egin{matrix}
cos heta & sin heta -sin heta & cos heta
end{matrix}
ight]
]
角度与弧度互转
弧度:Math.PI / 180 * deg
角度:180 / Math.PI * radian
div {
width: 100px;
height: 100px;
background: red;
transform:matrix(0.7853981633974483,0.7853981633974483,-0.7853981633974483,0.7853981633974483,0,0);
transform: rotate(45deg);
}
3D旋转
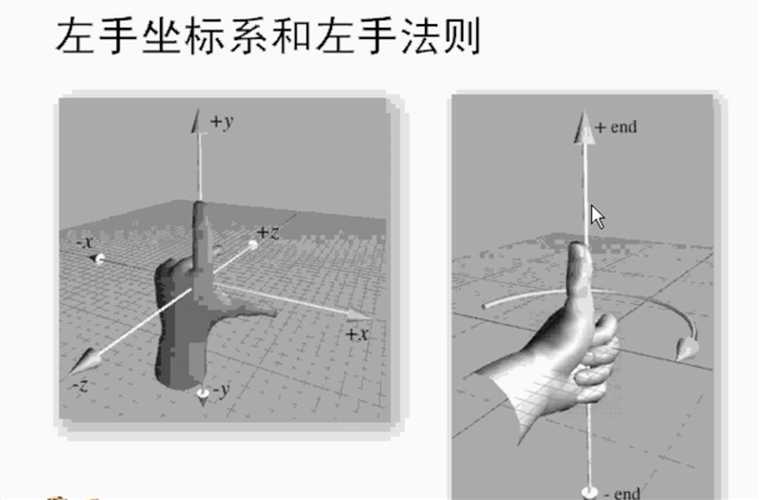
左手坐标系和左手法则
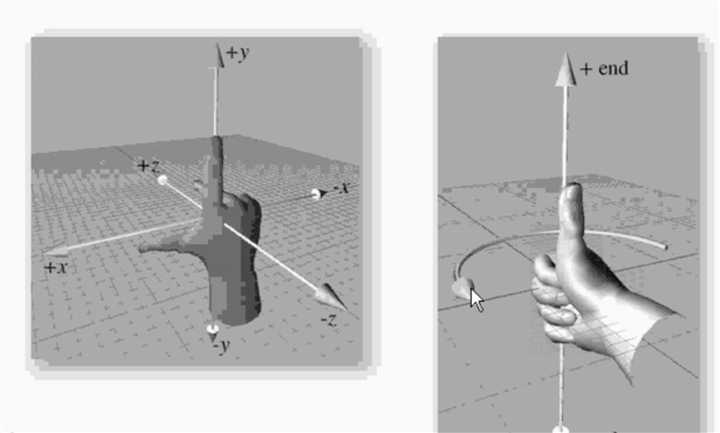
右手坐标系和右手法则
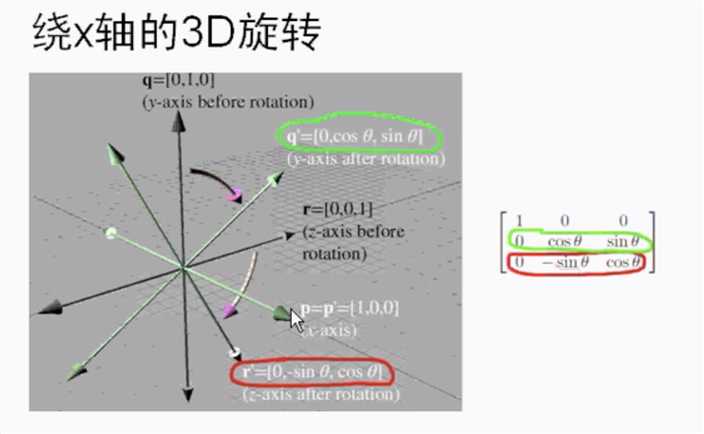
绕x轴旋转
[left[
egin{matrix}
x \\
y z
end{matrix}
ight] imes
left[
egin{matrix}
1 & 0 & 0 � & cos heta & sin heta � & -sin heta & cos heta
end{matrix}
ight]
]
绕y轴旋转
[left[
egin{matrix}
x \\
y z
end{matrix}
ight] imes
left[
egin{matrix}
cos heta & 0 & -sin heta � & 1 & 0 sin heta & 0 & cos heta
end{matrix}
ight]
]
div {
width: 100px;
height: 100px;
background: red;
transform: matrix3d(
0.7853981633974483,0,-0.7853981633974483,0,
0,1,0,0,
0.7853981633974483,0,0.7853981633974483,0,
0,0,0,1
);
}
绕z轴旋转
[left[
egin{matrix}
x \\
y z
end{matrix}
ight] imes
left[
egin{matrix}
cos heta & sin heta & 0 -sin heta & cos heta & 0 � & 0 & 1
end{matrix}
ight]
]
以上是关于线性变换的主要内容,如果未能解决你的问题,请参考以下文章