30 双向链表的实现

Posted 2020-12-11 lh03061238

原文：https://www.cnblogs.com/wanmeishenghuo/p/9655599.html  参考狄泰软件相关教程

 

 

 由上图可以看出来，插入和遍历的时间复杂度是不一样的。

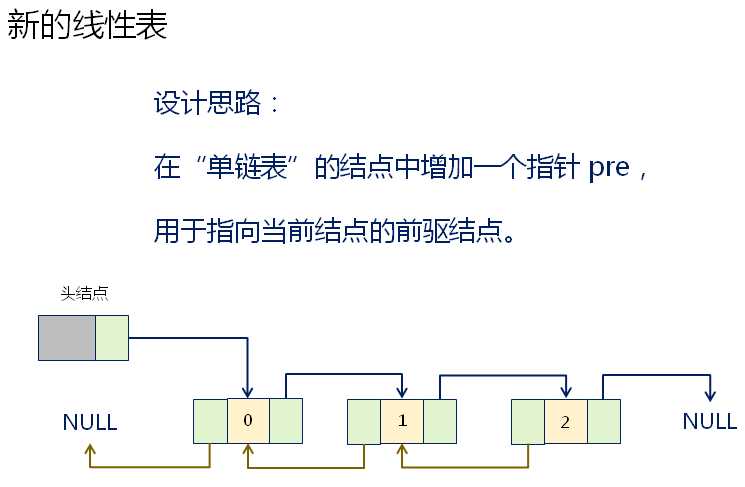
这样不管游标在哪一个位置上，都可以通过后继或者前驱指针任意访问。

双向链表的继承层次：

 

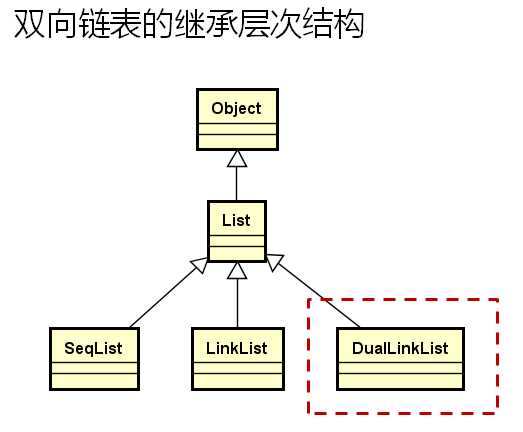
 单链表和双向链表应该是兄弟关系，而不应该是继承关系，因为它们的内部机制是完全不同的了。

 插入新节点图解：

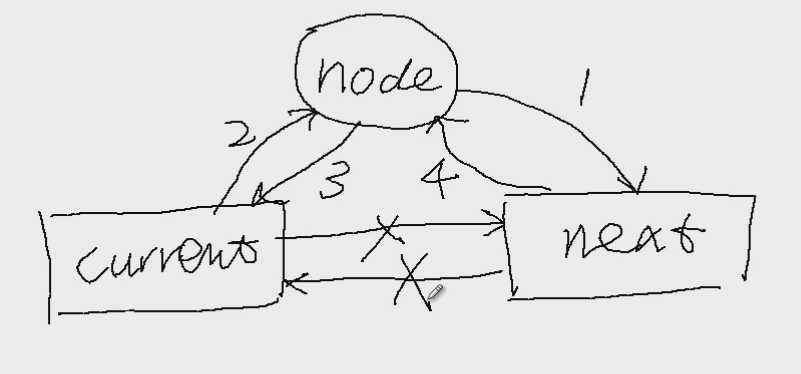
删除节点的步骤：

 

 

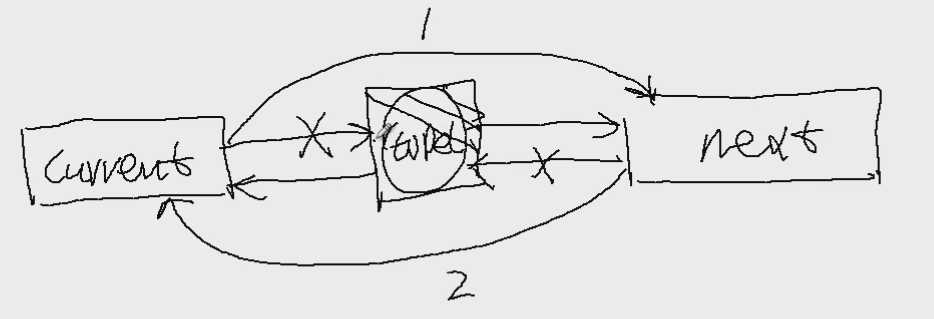
添加DualLinkList.h文件：

#ifndef DUALLINKLIST_H
#define DUALLINKLIST_H

#include "List.h"
#include "Exception.h"

namespace DTLib
{

template < typename T >
class DualLinkList : public List<T>
{
protected:
    struct Node : public Object
    {
        T value;
        Node* next;
        Node* pre;
    };

    mutable struct : public Object
    {
        char reserved[sizeof(T)];
        Node* next;
        Node* pre;
    }m_header;

    int m_length;
    int m_step;
    Node* m_current;

    Node* position(int i) const    //  O(n)
    {
        Node* ret = reinterpret_cast<Node*>(&m_header);

        for(int p = 0; p < i; p++)
        {
            ret = ret->next;
        }

        return ret;
    }

    virtual Node* create()
    {
        return new Node();
    }

    virtual void destroy(Node* pn)
    {
        delete pn;
    }

public:
    DualLinkList()
    {
        m_header.next = NULL;
        m_header.pre = NULL;
        m_length = 0;
        m_step = 1;
        m_current = NULL;
    }

    bool insert(const T& e)
    {
        return insert(m_length, e);
    }

    bool insert(int i, const T& e)   // O(n)
    {
        bool ret = ((0 <= i) && (i <= m_length));

        if( ret )
        {
            Node* node = create();

            if( node != NULL )
            {
                Node* current = position(i);
                Node* next = current->next; //即将插入的节点的后继节点

                node->value = e;

                node->next = next;  //第1步
                current->next = node; //第2步

                if( current != reinterpret_cast<Node*>(&m_header))  //判断是否是头结点
                {
                    node->pre = current;  // 第3步
                }
                else
                {
                    node->pre = NULL;
                }

                if( next != NULL )
                {
                    next->pre = node;   //第4步
                }

                m_length++;
            }
            else
            {
                THROW_EXCEPTION(NoEnoughMemoryException, "No memery to insert new element...");
            }
        }

        return ret;
    }

    bool remove(int i)   // O(n)
    {
        bool ret = ((0 <= i) && (i < m_length));

        if( ret )
        {
            Node* current = position(i);
            Node* toDel = current->next;
            Node* next = toDel->next;

            if( m_current == toDel )
            {
                m_current = next;
            }

            current->next = next;  //第1步

            if( next != NULL )
            {
                next->pre = toDel->pre;  //第2步
            }

            m_length--;

            destroy(toDel);

        }

        return ret;
    }

    bool set(int i, const T& e)   //  O(n)
    {
        bool ret = ((0 <= i) && (i < m_length));

        if( ret )
        {
            position(i)->next->value = e;
        }

        return ret;
    }

    virtual T get(int i) const   // O(n)
    {
        T ret;

        if( get(i, ret) )
        {
            return ret;
        }
        else
        {
            THROW_EXCEPTION(IndexOutOfBoundsException, "Invalid parameter i to get element ...");
        }

        return ret;
    }

    bool get(int i, T& e) const    // O(n)
    {
        bool ret = ((0 <= i) && (i < m_length));

        if( ret )
        {
            e = position(i)->next->value;
        }

        return ret;
    }

    int find(const T& e) const    //  O(n)
    {
        int ret = -1;
        int i = 0;

        Node* node = m_header.next;

        while( node )
        {
            if( node->value == e )
            {
                ret = i;
                break;
            }
            else
            {
                node = node->next;
                i++;
            }
        }

        return ret;
    }

    int length() const   // O(1)
    {
        return m_length;
    }

    void clear()    //  O(n)
    {
        while( m_length > 0 )
        {
            remove(0);
        }
    }

    virtual bool move(int i, int step = 1)
    {
        bool ret = (0 <= i) && (i < m_length) && (step > 0);

        if( ret )
        {
            m_current = position(i)->next;
            m_step = step;
        }

        return ret;
    }

    virtual bool end()
    {
        return (m_current == NULL);
    }

    virtual T current()
    {
        if( !end() )
        {
            return m_current->value;
        }
        else
        {
            THROW_EXCEPTION(InvalidOperationException, "No value at current position ...");
        }
    }

    virtual bool next()   //每次移动step步
    {
        int i = 0;

        while((i < m_step) && !end())
        {
            m_current = m_current->next;
            i++;
        }

        return (i == m_step);
    }

    virtual bool pre()
    {
        int i = 0;

        while((i < m_step) && !end())
        {
            m_current = m_current->pre;
            i++;
        }

        return (i == m_step);
    }

    ~DualLinkList()   //  O(n)
    {
        clear();
    }
};

}

#endif // DUALLINKLIST_H

和LinkList的不同只在于Node的元素，我们新添加了pre成员。

insert函数和remove函数是改动最大的。

新增加了pre函数。

测试程序如下：

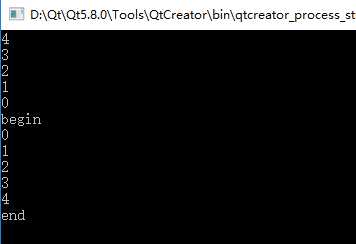
#include <iostream>
#include "DualLinkList.h"

using namespace std;
using namespace DTLib;


int main()
{
    DualLinkList<int> dl;

    for(int i = 0; i < 5; i++)
    {
        dl.insert(0, i);
    }

    for(int i = 0; i < dl.length(); i++)
    {
        cout << dl.get(i) << endl;
    }

    cout << "begin" << endl;

    for(dl.move(dl.length() - 1); !dl.end(); dl.pre())
    {
        cout << dl.current() << endl;
    }

    cout << "end" << endl;

    return 0;
}

　

第一个for循环时间复杂度是O(n*n)，第二个for循环的时间复杂度是O(n)。

结果如下：

 

 

测试程序2：

#include <iostream>
#include "DualLinkList.h"

using namespace std;
using namespace DTLib;


int main()
{
    DualLinkList<int> dl;

    for(int i = 0; i < 5; i++)
    {
        dl.insert(0, i);
        dl.insert(0, 5);
    }

    for(dl.move(0); !dl.end(); dl.next())
    {
        cout << dl.current() << endl;
    }

    cout << "begin" << endl;

    dl.move(dl.length() - 1);

    while(!dl.end())
    {
        if( dl.current() == 5 )
        {
            cout << dl.current() << endl;

            dl.remove(dl.find(dl.current()));
        }
        else
        {
            dl.pre();
        }
    }

    cout << "end" << endl;

    for(dl.move(0); !dl.end(); dl.next())
    {
        cout << dl.current() << endl;
    }

    return 0;
}

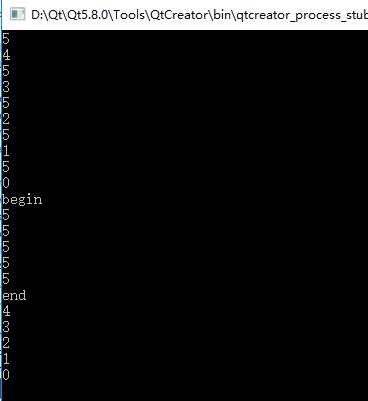
结果如下：

 

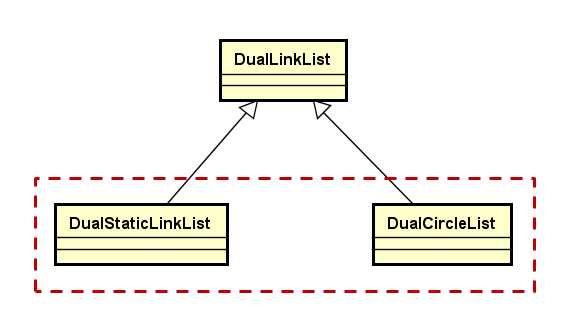
小结：

 

 

 

 双向链表的子类：