P3355 骑士共存问题最小点覆盖网络流24题

Posted 2020-12-11 orangeko

 

 

 

思路

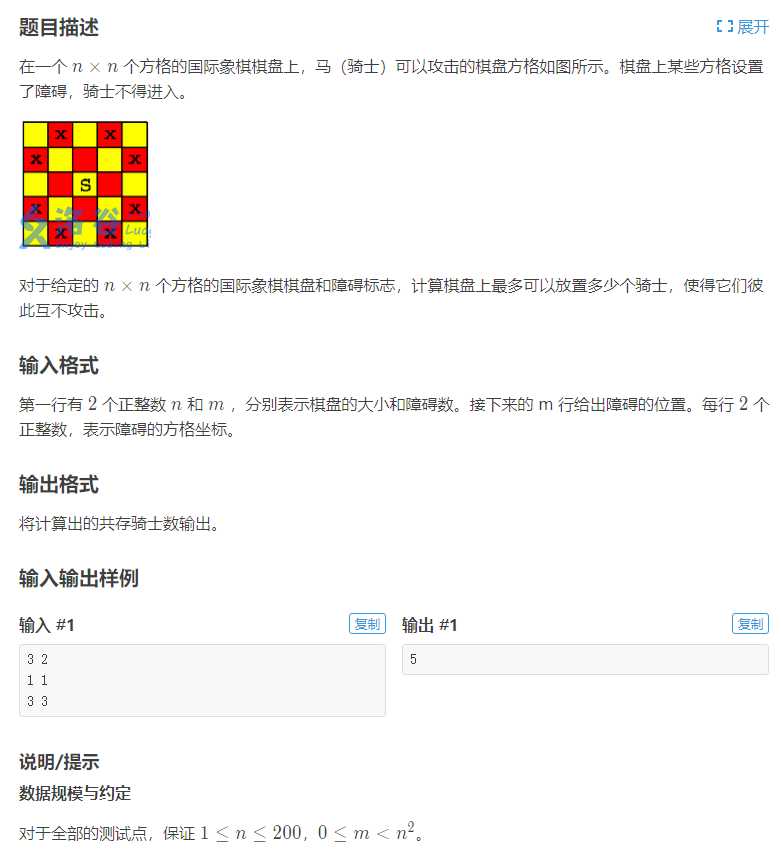
　　显然棋盘上的每个点有三种形态：障碍物，马，已存的马能跳到的不能放马的点

　　显然1、3在处理时可以归为一类，则共有两种点态。

　　所以这题可以看成一个二分图来做

　　每个马最多能覆盖棋盘上的八个点位

　　这就形似最大独立集的概念了

　　把所有独立集和障碍物都染色，剩下的就是就是可以放马的点

 

CODE

 

  1 #include <bits/stdc++.h>
  2 
  3 using namespace std;
  4 
  5 
  6 
  7 const int maxn = 1e6 + 7;
  8 
  9 const int inf = 0x3f3f3f3f;
 10 
 11 
 12 
 13 template<class T>inline void read(T &res)
 14 
 15 {
 16 
 17     char c;T flag=1;
 18 
 19     while((c=getchar())<‘0‘||c>‘9‘)if(c==‘-‘)flag=-1;res=c-‘0‘;
 20 
 21     while((c=getchar())>=‘0‘&&c<=‘9‘)res=res*10+c-‘0‘;res*=flag;
 22 
 23 }
 24 
 25 
 26 
 27 struct edge{int from,to,cap,flow;};
 28 
 29 int s, t, n, m;
 30 
 31 struct isap
 32 
 33 {
 34 
 35     int n,s,t,p[maxn],d[maxn],cur[maxn],num[maxn];
 36 
 37     bool vis[maxn];
 38 
 39     vector<int>g[maxn];
 40 
 41     vector<edge>edges;
 42 
 43     void init(int n,int s,int t) {
 44 
 45         this->n = n;
 46 
 47         this->s = s;
 48 
 49         this->t = t;
 50 
 51         for(int i = 1;i <= n;i++) g[i].clear();
 52 
 53         edges.clear();
 54 
 55     }
 56 
 57     void addegde(int from,int to,int cap) {
 58 
 59         edges.push_back((edge){from, to, cap, 0});
 60 
 61         edges.push_back((edge){to, from, 0, 0});
 62 
 63         int m = edges.size();
 64 
 65         g[from].push_back(m-2);
 66 
 67         g[to].push_back(m-1);
 68 
 69     }
 70 
 71 
 72 
 73     int augment() {///找增广路
 74 
 75         int x = t,a = inf;
 76 
 77         while(x!=s) {
 78 
 79             a = min(a, edges[p[x]].cap - edges[p[x]].flow);
 80 
 81             x = edges[p[x]].from;
 82 
 83         }
 84 
 85         x=t;
 86 
 87         while(x != s) {
 88 
 89             edges[p[x]].flow += a;
 90 
 91             edges[p[x]^1].flow = -a;
 92 
 93             x = edges[p[x]].from;
 94 
 95         }
 96 
 97         return a;
 98 
 99     }
100 
101     int maxflow() {///更新最大流
102 
103         int flow = 0;
104 
105         memset(num, 0, sizeof(num));
106 
107         memset(cur, 0, sizeof(cur));
108 
109         for(int i = 1; i <= n; i++) num[d[i]]++;
110 
111         int x = s;
112 
113         while(d[s] < n) {///最长的一条链上，最大的下标是nv-1，如果大于等于nv说明已断层
114 
115             if(x == t) {
116 
117                 flow += augment();
118 
119                 x = s;//回退
120 
121             }
122 
123             bool ok = 0;
124 
125             for(int i = cur[x]; i < g[x].size(); i++) {
126 
127                 edge &e = edges[g[x][i]];
128 
129                 if(d[x] == d[e.to] + 1 && e.cap > e.flow) {
130 
131                     p[e.to] = g[x][i];
132 
133                     cur[x] = i;x = e.to;
134 
135                     ok = 1;
136 
137                     break;
138 
139                 }
140 
141             }
142 
143             if(!ok) {
144 
145                 int m = n-1;
146 
147                 for(int i = 0; i < g[x].size();i++) {
148 
149                     edge &e=edges[g[x][i]];
150 
151                     if(e.cap>e.flow) m=min(m,d[e.to]);
152 
153                 }
154 
155                 num[d[x]]--;
156 
157                 if(!num[d[x]]) break;
158 
159                 d[x] = m+1;
160 
161                 num[d[x]]++;
162 
163                 cur[x] = 0;
164 
165                 if(x != s) x = edges[p[x]].from;
166 
167             }
168 
169         }
170 
171         return flow;
172 
173     }
174 
175 }ISAP;
176 
177 inline int id(int x, int y) {
178     return (x-1) * n + y;
179 }
180 
181 int a[507][507];
182 
183 int dr[8] = {-2, -2, -1, -1, 1, 1, 2, 2};
184 int dc[8] = {1, -1, 2, -2, 2, -2, 1, -1};
185 
186 int main()
187 {
188     read(n); read(m);
189     
190     memset(a, 0, sizeof(a));
191     s = 0, t = n * n + 1;
192     ISAP.init(n * n * 2, s, t);
193     for ( int i = 1; i <= m; ++i ) {
194         int x, y;
195         read(x); read(y);
196         a[x][y] = 1;
197     }
198     for ( int i = 1; i <= n; ++i ) {
199         for ( int j = 1; j <= n; ++j ) {
200             if(a[i][j])
201                 continue;
202             if((i + j) & 1) {
203                 ISAP.addegde(s, id(i, j), 1);
204                 for ( int k = 0; k <= 7; ++k ) {
205                     int x = i + dr[k], y = j + dc[k];
206                     if(x < 1 || x > n || y < 1 || y > n) {
207                         continue;
208                     }
209                     ISAP.addegde(id(i, j), id(x, y), inf);
210                 }
211             }
212             else {
213                 ISAP.addegde(id(i, j), t, 1);
214             }
215         }
216     }
217     int maxflow = ISAP.maxflow();
218     //dbg(maxflow);
219     int ans = n * n - m - maxflow;
220     cout << ans << endl;
221     return 0;
222 }

View Code