在空域对图片加性噪声的去噪处理
Posted cyssmile
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了在空域对图片加性噪声的去噪处理相关的知识，希望对你有一定的参考价值。
此部分实验包含：
1、算术均值滤波去噪算法
2、几何均值滤波去噪算法
3、谐波均值滤波去噪算法
4、反谐波均值滤波去噪算法
5、中值滤波去噪算法
6、自适应中值滤波去噪算法
7、自适应局部降低噪声滤波器去噪算法
当一副图片中唯一存在的退化是噪声时，就有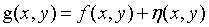
和
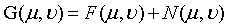这两个公式，其中
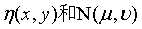是噪声项，且是未知的。所以从
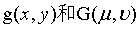中减去噪声项是不可能的。这里我们只讨论存在加性噪声，我们可以使用空间滤波的方法来去噪。
1、算术均值滤波去噪算法
这是一种简单的均值滤波器，令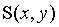
是中心点在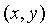
处，大小为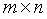
的矩阵子图像的一组坐标。算术均值就是计算
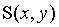定义区域中被污染图像
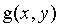的均值，即是
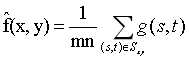
这个操作可以使用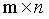
的空间滤波器实现，滤波器的所有的系数都为其值的
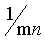，这种方式可以模糊结果，但同时也降低噪声。
1.1、 算术均值滤波编码实现
void arithmeticMeanBlur(Mat& src, Mat& dst, int m, int n)
{
double weight = 1.0 / ((double)m * (double)n);
//根据m*n 大小的核填充处理图像
//填充边缘大小
int row = src.rows;
int col = src.cols;
int rowPadding = getBordValue(row, 1, n);
int colPadding = getBordValue(col, 1, m);
Mat t_src;
copyMakeBorder(src, t_src, rowPadding, rowPadding, colPadding, colPadding, BORDER_DEFAULT);
//进行算术均值滤波
int channels = src.channels();
int cols = t_src.cols - rowPadding;
int rows = t_src.rows - colPadding;
for (int i = rowPadding; i < rows; i++) {
for (int j = colPadding; j < cols; j++) {
double sum[3] = { 0 };
for (int k = -rowPadding; k <= rowPadding; k++) {
for (int m = -colPadding; m <= colPadding; m++) {
if (channels == 1) {
sum[0] += weight * t_src.at<uchar>(i + k, j + m);
}
else if (channels == 3) {
Vec3b rgb = t_src.at<Vec3b>(i + k, j + m);
sum[0] += weight* rgb[0];
sum[1] += weight * rgb[1];
sum[2] += weight * rgb[2];
}
}
}
//限定像素值在0-255之间
for (int i = 0; i < channels; i++) {
if (sum[i] < 0)
sum[i] = 0;
else if (sum[i] > 255)
sum[i] = 255;
}
//
if (channels == 1) {
dst.at<uchar>(i - rowPadding, j - colPadding) = static_cast<uchar>(sum[0]);
}
else if (channels == 3) {
Vec3b rgb;
rgb[0] = static_cast<uchar>(sum[0]);
rgb[1] = static_cast<uchar>(sum[1]);
rgb[2] = static_cast<uchar>(sum[2]);
dst.at<Vec3b>(i - rowPadding, j - colPadding) = rgb;
}
}
}
}
void comparedMeanBlur(Mat& sapSrc, Mat& sSrc, Mat& pSrc, Mat& gSrc)
{
//5*5 的算术均值滤波处理椒盐噪声
Mat dst1 = sapSrc.clone();
arithmeticMeanBlur(sapSrc, dst1, 5, 5);
imshow("5*5算术均值处理椒盐噪声结果", dst1);
//5*5 的算术均值滤波处理椒噪声
Mat dst2 = pSrc.clone();
arithmeticMeanBlur(pSrc, dst2, 5, 5);
imshow("5*5算术均值处理椒噪声结果", dst2);
//5*5 的算术均值滤波处理盐噪声
Mat dst3 = sSrc.clone();
arithmeticMeanBlur(sSrc, dst3, 5, 5);
imshow("5*5算术均值处理盐噪声结果", dst3);
//5*5 的算术均值滤波处理高斯噪声
Mat dst4 = gSrc.clone();
arithmeticMeanBlur(gSrc, dst4, 5, 5);
imshow("5*5算术均值处理高斯噪声结果", dst4);
}
3.1.2 算术均值滤波实验效果
原图
添加噪声的图片,这里椒盐噪声、胡椒噪声、盐粒噪声比例为0.1， 高斯噪声 均值为15 方差为25。
5*5 算术均值滤波的结果
2 几何均值滤波器
使用几何均值滤波器复原的一副图片的表达式：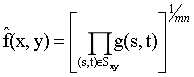
其中，每个复原的像素由窗口中像素的乘积的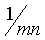
次幂给出。
2.1 几何均值滤波编码实现
void geometricMean(Mat& src, Mat& dst, int m, int n)
{
double weight = 1.0 / ((double)m * (double)n);
//根据m*n 大小的核填充处理图像
//填充边缘大小
int row = src.rows;
int col = src.cols;
int rowPadding = getBordValue(row, 1, n);
int colPadding = getBordValue(col, 1, m);
//这里不要直接填充src,因为这里是引用，可能后面的实验会重复填充
Mat t_src;
copyMakeBorder(src, t_src, rowPadding, rowPadding, colPadding, colPadding, BORDER_DEFAULT);
int channels = src.channels();
int cols = t_src.cols - rowPadding;
int rows = t_src.rows - colPadding;
for (int i = rowPadding; i < rows; i++) {
for (int j = colPadding; j < cols; j++) {
double sum[3] = { 1,1,1 };
for (int k = -rowPadding; k <= rowPadding; k++) {
for (int m = -colPadding; m <= colPadding; m++) {
if (channels == 1) {
sum[0] *= (double)t_src.at<uchar>(i + k, j + m);
}
else if (channels == 3) {
Vec3b rgb = t_src.at<Vec3b>(i + k, j + m);
sum[0] *= rgb[0];
sum[1] *= rgb[1];
sum[2] *= rgb[2];
}
}
}
//乘以1/mn次幂
for (int i = 0; i < channels; i++) {
sum[i] = pow(sum[i], weight);
}
//限定像素值在0-255之间
for (int i = 0; i < channels; i++) {
if (sum[i] < 0)
sum[i] = 0;
else if (sum[i] > 255)
sum[i] = 255;
}
//
if (channels == 1) {
dst.at<uchar>(i - rowPadding, j - colPadding) = static_cast<uchar>(sum[0]);
}
else if (channels == 3) {
Vec3b rgb;
rgb[0] = static_cast<uchar>(sum[0]);
rgb[1] = static_cast<uchar>(sum[1]);
rgb[2] = static_cast<uchar>(sum[2]);
dst.at<Vec3b>(i - rowPadding, j - colPadding) = rgb;
}
}
}
}
void comparedGeometricMeanBlur(Mat& sapSrc, Mat& sSrc, Mat& pSrc, Mat& gSrc)
{
//5*5 的几何均值滤波处理椒盐噪声
Mat dst1 = sapSrc.clone();
geometricMean(sapSrc, dst1, 5, 5);
imshow("5*5几何均值处理椒盐噪声结果", dst1);
//5*5 的几何均值滤波处理椒噪声
Mat dst2 = pSrc.clone();
geometricMean(pSrc, dst2, 5, 5);
imshow("5*5几何均值处理椒噪声结果", dst2);
//5*5 的几何均值滤波处理盐噪声
Mat dst3 = sSrc.clone();
geometricMean(sSrc, dst3, 5, 5);
imshow("5*5几何均值处理盐噪声结果", dst3);
//5*5 的几何均值滤波处理高斯噪声
Mat dst4 = gSrc.clone();
geometricMean(gSrc, dst4, 5, 5);
imshow("5*5几何均值处理高斯噪声结果", dst4);
}
2.2 几何均值处理结果
原图
添加噪声的图片,这里椒盐噪声、胡椒噪声、盐粒噪声比例为0.1， 高斯噪声 均值为15 方差为25。
5*5 几何均值处理图片结果
- 结果分析：由于这种方式处理图片可以保留细节信息，所以对胡椒，盐粒噪声更加敏感，所有处理结果中前两个效果并不是很好。其次这种方式处理计算量大。
3谐波均值滤波
谐波均值滤波操作给出如下的表达式：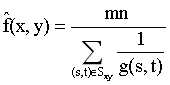
谐波均值对盐粒噪声，高斯噪声处理的效果比较好，但是不善于处理胡椒噪声。
3.1 谐波均值滤波编码实现
/*
* 谐波均值
* 谐波均值 适合处理盐噪声，不适合处理胡椒噪声，也擅长处理高斯噪声
*/
void harmonicMeanBlur(Mat& src, Mat& dst, int m, int n)
{
double weight = ((double)m * (double)n);
//根据m*n 大小的核填充处理图像
//填充边缘大小
int row = src.rows;
int col = src.cols;
int rowPadding = getBordValue(row, 1, n);
int colPadding = getBordValue(col, 1, m);
//这里不要直接填充src,因为这里是引用，可能后面的实验会重复填充
Mat t_src;
copyMakeBorder(src, t_src, rowPadding, rowPadding, colPadding, colPadding, BORDER_DEFAULT);
int channels = src.channels();
int cols = t_src.cols - rowPadding;
int rows = t_src.rows - colPadding;
for (int i = rowPadding; i < rows; i++) {
for (int j = colPadding; j < cols; j++) {
double sum[3] = { 0,0,0 };
for (int k = -rowPadding; k <= rowPadding; k++) {
for (int m = -colPadding; m <= colPadding; m++) {
if (channels == 1) {
sum[0] += 1.0/(double)t_src.at<uchar>(i + k, j + m);
}
else if (channels == 3) {
Vec3b rgb = t_src.at<Vec3b>(i + k, j + m);
sum[0] += 1.0/rgb[0];
sum[1] += 1.0/rgb[1];
sum[2] += 1.0/rgb[2];
}
}
}
//mn/sum[]
for (int i = 0; i < channels; i++) {
sum[i] = weight/sum[i];
}
//限定像素值在0-255之间
for (int i = 0; i < channels; i++) {
if (sum[i] < 0)
sum[i] = 0;
else if (sum[i] > 255)
sum[i] = 255;
}
//
if (channels == 1) {
dst.at<uchar>(i - rowPadding, j - colPadding) = static_cast<uchar>(sum[0]);
}
else if (channels == 3) {
Vec3b rgb;
rgb[0] = static_cast<uchar>(sum[0]);
rgb[1] = static_cast<uchar>(sum[1]);
rgb[2] = static_cast<uchar>(sum[2]);
dst.at<Vec3b>(i - rowPadding, j - colPadding) = rgb;
}
}
}
}
void comparedHarmonicMeanBlur(Mat& sapSrc, Mat& sSrc, Mat& pSrc, Mat& gSrc)
{
//5*5 的谐波均值滤波处理椒盐噪声
Mat dst1 = sapSrc.clone();
harmonicMeanBlur(sapSrc, dst1, 5, 5);
imshow("5*5谐波均值处理椒盐噪声结果", dst1);
//5*5 的几何均值滤波处理椒噪声
Mat dst2 = pSrc.clone();
harmonicMeanBlur(pSrc, dst2, 5, 5);
imshow("5*5谐波均值处理椒噪声结果", dst2);
//5*5 的算术均值滤波处理盐噪声
Mat dst3 = sSrc.clone();
harmonicMeanBlur(sSrc, dst3, 5, 5);
imshow("5*5谐波均值处理盐噪声结果", dst3);
//5*5 的算术均值滤波处理高斯噪声
Mat dst4 = gSrc.clone();
harmonicMeanBlur(gSrc, dst4, 5, 5);
imshow("5*5谐波均值处理高斯噪声结果", dst4);
}
3.2 谐波均值滤波实验效果
原图
添加噪声的图片,这里椒盐噪声、胡椒噪声、盐粒噪声比例为0.1， 高斯噪声 均值为15 方差为25。
5*5谐波均值处理效果
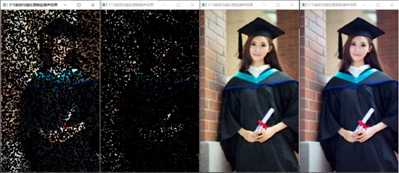
结果分析：我们可以明显看出谐波均值在处理盐粒噪声和高斯噪声上有很好的效果，但是处理椒盐噪声，胡椒噪声的效果很差。
4、逆谐波均值滤波器
逆谐波均值滤波器基于如下产生一副复原的图像：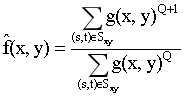
其中Q为滤波器的阶数，这种滤波器适合在实际中处理椒盐噪声。当Q为正的时候可以处理胡椒噪声，当Q为负的时候，可以消除盐粒噪声，当Q=0时，就是算术均值滤波器。注意逆谐波均值滤波器无法同时消除胡椒和盐粒噪声。
4.1 逆谐波均值滤波器代码实现
void inverseHarmonicMeanBlure(Mat& src, Mat& dst, int m, int n, double Q)
{
double weight = ((double)m * (double)n);
//根据m*n 大小的核填充处理图像
//填充边缘大小
int row = src.rows;
int col = src.cols;
int rowPadding = getBordValue(row, 1, n);
int colPadding = getBordValue(col, 1, m);
//这里不要直接填充src,因为这里是引用，可能后面的实验会重复填充
Mat t_src;
copyMakeBorder(src, t_src, rowPadding, rowPadding, colPadding, colPadding, BORDER_DEFAULT);
int channels = src.channels();
int cols = t_src.cols - rowPadding;
int rows = t_src.rows - colPadding;
for (int i = rowPadding; i < rows; i++) {
for (int j = colPadding; j < cols; j++) {
double sum[3] = { 0,0,0 };
double sum1[3] = { 0,0,0 };
for (int k = -rowPadding; k <= rowPadding; k++) {
for (int m = -colPadding; m <= colPadding; m++) {
if (channels == 1) {
sum[0] += pow( (double)t_src.at<uchar>(i + k, j + m),Q+1);
sum1[0] += pow((double)t_src.at<uchar>(i + k, j + m), Q);
}
else if (channels == 3) {
Vec3b rgb = t_src.at<Vec3b>(i + k, j + m);
sum[0] += pow(rgb[0],Q+1);
sum[1] += pow(rgb[1], Q + 1);
sum[2] += pow(rgb[2], Q + 1);
sum1[0] += pow(rgb[0], Q);
sum1[1] += pow(rgb[1], Q);
sum1[2] += pow(rgb[2], Q);
}
}
}
double result[3] = { 0,0,0 };
//限定像素值在0-255之间
for (int t = 0; t < channels; t++) {
result[t] = (double)sum[t] / sum1[t];
if (result[t] < 0)
result[t] = 0;
else if (result[t] > 255)
result[t] = 255;
}
//
if (channels == 1) {
dst.at<uchar>(i - rowPadding, j - colPadding) = static_cast<uchar>(result[0]);
}
else if (channels == 3) {
Vec3b rgb;
rgb[0] = static_cast<uchar>(result[0]);
rgb[1] = static_cast<uchar>(result[1]);
rgb[2] = static_cast<uchar>(result[2]);
dst.at<Vec3b>(i - rowPadding, j - colPadding) = rgb;
}
}
}
}
void comparedInverseHarmonicMeanBlur(Mat& sapSrc, Mat& sSrc, Mat& pSrc, Mat& gSrc, double Q)
{
//5*5 的反谐波均值滤波处理椒盐噪声
Mat dst1 = sapSrc.clone();
inverseHarmonicMeanBlure(sapSrc, dst1, 5, 5, Q);
imshow("5*5反谐波均值处理椒盐噪声结果", dst1);
//5*5 的反谐波均值滤波处理椒噪声
Mat dst2 = pSrc.clone();
inverseHarmonicMeanBlure(pSrc, dst2, 5, 5, Q);
imshow("5*5反谐波均值处理椒噪声结果", dst2);
//5*5 的反谐波均值滤波处理盐噪声
Mat dst3 = pSrc.clone();
inverseHarmonicMeanBlure(sSrc, dst3, 5, 5, Q);
imshow("5*5反谐波均值处理盐粒噪声结果", dst3);
//5*5 的反谐波滤波处理高斯噪声
Mat dst4 = gSrc.clone();
inverseHarmonicMeanBlure(gSrc, dst3, 5, 5, Q);
imshow("5*5反谐波均值处理高斯噪声结果", dst4);
}
4.2 逆谐波均值滤波实验效果
原图
添加噪声的图片,这里椒盐噪声、胡椒噪声、盐粒噪声比例为0.1， 高斯噪声 均值为15 方差为25。
当 Q = 1时，对胡椒噪声处理效果明显。
当Q = -1时，对盐粒噪声处理效果明显。
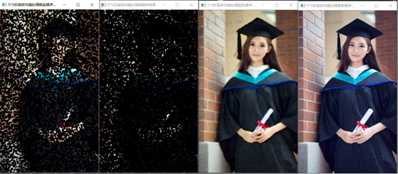
当Q = 0时，这时候相当于算术均值滤波。
5 中值滤波器
中值滤波是基于统计排序的滤波器，它使用一个像素的领域的中值来代替该点的像素值，即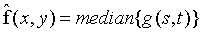
这种方式可以有效处理椒盐噪声，盐粒噪声，胡椒噪声。
5.1 中值滤波器编码实现
/*
*中值滤波
* 中值滤波对处理椒盐噪声 胡椒 盐粒噪声的效果很好
*/
void iMidBlur(Mat& src, Mat& dst, int m, int n)
{
double weight = ((double)m * (double)n);
//根据m*n 大小的核填充处理图像
//填充边缘大小
int row = src.rows;
int col = src.cols;
int rowPadding = getBordValue(row, 1, n);
int colPadding = getBordValue(col, 1, m);
//这里不要直接填充src,因为这里是引用，可能后面的实验会重复填充
Mat t_src;
copyMakeBorder(src, t_src, rowPadding, rowPadding, colPadding, colPadding, BORDER_DEFAULT);
int channels = src.channels();
int cols = t_src.cols - rowPadding;
int rows = t_src.rows - colPadding;
for (int i = rowPadding; i < rows; i++) {
for (int j = colPadding; j < cols; j++) {
vector<double> mid0,mid1,mid2;
mid0.clear();
mid1.clear();
mid2.clear();
for (int k = -rowPadding; k <= rowPadding; k++) {
for (int m = -colPadding; m <= colPadding; m++) {
if (channels == 1) {
mid0.push_back((double)t_src.at<uchar>(i + k, j + m));
}
else if (channels == 3) {
Vec3b rgb = t_src.at<Vec3b>(i + k, j + m);
mid0.push_back((double)rgb[0]);
mid1.push_back((double)rgb[1]);
mid2.push_back((double)rgb[2]);
}
}
}
sort(mid0.begin(), mid0.end());
sort(mid1.begin(), mid1.end());
sort(mid2.begin(), mid2.end());
int r = m * n / 2;
if (channels == 1) {
dst.at<uchar>(i - rowPadding, j - colPadding) = static_cast<uchar>(mid0[r]);
}
else if (channels == 3) {
Vec3b rgb;
rgb[0] = static_cast<uchar>(mid0[r]);
rgb[1] = static_cast<uchar>(mid1[r]);
rgb[2] = static_cast<uchar>(mid2[r]);
dst.at<Vec3b>(i - rowPadding, j - colPadding) = rgb;
}
}
}
}
void comparedMidBlur(Mat& sapSrc, Mat& sSrc, Mat& pSrc, Mat& gSrc)
{
//5*5 的中值滤波处理椒盐噪声
Mat dst1 = sapSrc.clone();
iMidBlur(sapSrc, dst1, 5, 5);
imshow("5*5中值滤波处理椒盐噪声结果", dst1);
//5*5 的中值滤波处理椒噪声
Mat dst2 = pSrc.clone();
iMidBlur(pSrc, dst2, 5, 5);
imshow("5*5中值滤波处理椒噪声结果", dst2);
//5*5 的中值滤波处理盐噪声
Mat dst3 = pSrc.clone();
iMidBlur(sSrc, dst3, 5, 5);
imshow("5*5中值滤波处理盐粒噪声结果", dst3);
//5*5 的中值滤波处理高斯噪声
Mat dst4 = gSrc.clone();
iMidBlur(gSrc, dst3, 5, 5);
imshow("5*5中值滤波处理高斯噪声结果", dst4);
}
5.2 中值滤波实验效果
原图
添加噪声的图片,这里椒盐噪声、胡椒噪声、盐粒噪声比例为0.1， 高斯噪声 均值为15 方差为25。
5*5中值滤波器
结果分析：中值滤波对脉冲型噪声处理效果很好。
6 自适应局部降低噪声滤波
自适应局部降低噪声滤波可以由如下的公式定义：
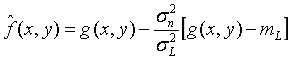
其中，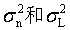
分别为全局的方差和选择窗口的局部方差，
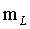为窗口的均值。这种方式主要用于处理加性高斯噪声。
6.1 自适应局部降低噪声滤波代码实现
/*
* 自适应均值滤波器
*/
void adaptiveMeanBlur(Mat& src, Mat& dst, int n, int m)
{
//根据m*n 大小的核填充处理图像
//填充边缘大小
int row = src.rows;
int col = src.cols;
int rowPadding = getBordValue(row, 1, n);
int colPadding = getBordValue(col, 1, m);
//这里不要直接填充src,因为这里是引用，可能后面的实验会重复填充
Mat t_src;
copyMakeBorder(src, t_src, rowPadding, rowPadding, colPadding, colPadding, BORDER_DEFAULT);
//计算全局的方差
vector<Mat> splitMat;
split(src,splitMat);
double stdDevValue[3] = { 0,0,0 };
int channels = src.channels();
for (int i = 0; i < channels;i++)
{
Mat mt, dt;
meanStdDev(splitMat[i], mt, dt);
stdDevValue[i] = pow(dt.at<double>(0, 0), 2);
}
int cols = t_src.cols - rowPadding;
int rows = t_src.rows - colPadding;
int roiSize = m * n;
for (int i = rowPadding; i < rows; i++) {
for (int j = colPadding; j < cols; j++) {
//先算选择的ROI区域的均值
double totalPiex[3] = { 0,0,0 };
for (int k = -rowPadding; k <= rowPadding; k++)
{
for (int m = -colPadding; m <= colPadding; m++)
{
if (channels == 1)
{
totalPiex[0] += (double)t_src.at<uchar>(i + k, j + m);
}
else {
Vec3b rgb = t_src.at<Vec3b>(i + k, j + m);
totalPiex[0] += (double)rgb[0];
totalPiex[1] += (double)rgb[1];
totalPiex[2] += (double)rgb[2];
}
}
}
for (int t = 0; t < channels; t++) {
//计算得到均值
totalPiex[t] = (double)totalPiex[t] / roiSize;
}
//接下来要算局部方差
double roiDev[3] = { 0,0,0 };
for (int k = -rowPadding; k <= rowPadding; k++) {
for (int m = -colPadding; m <= colPadding; m++) {
if (channels == 1) {
roiDev[0] += pow((double)t_src.at<uchar>(i + k, j + m)-totalPiex[0],2);
}
else if (channels == 3) {
Vec3b rgb = t_src.at<Vec3b>(i + k, j + m);
roiDev[0] += pow((double)rgb[0] - totalPiex[0], 2);
roiDev[1] += pow((double)rgb[1] - totalPiex[1], 2);
roiDev[2] += pow((double)rgb[2] - totalPiex[0], 2);
}
}
}
for (int t = 0; t < channels; t++) {
//计算得到方差
roiDev[t] = roiDev[t] / roiSize;
}
//计算每个像素的值 自适应均值法
double result[3] = { 0,0,0 };
for (int k = -rowPadding; k <= rowPadding; k++) {
for (int m = -colPadding; m <= colPadding; m++) {
if (channels == 1) {
result[0] = t_src.at<uchar>(i + k, j + m)-(stdDevValue[0]/roiDev[0])*(t_src.at<uchar>(i + k, j + m)-totalPiex[0]);
}
else if (channels == 3) {
Vec3b rgb = t_src.at<Vec3b>(i + k, j + m);
result[0] = rgb[0] - (stdDevValue[0] / roiDev[0]) * (rgb[0] - totalPiex[0]);
result[1] = rgb[1] - (stdDevValue[1] / roiDev[1]) * (rgb[1] - totalPiex[1]);
result[2] = rgb[2] - (stdDevValue[2] / roiDev[2]) * (rgb[2] - totalPiex[2]);
}
}
}
//限定像素值在0-255之间
for (int t = 0; t < channels; t++) {
if (result[t] < 0)
result[t] = 0;
else if (result[t] > 255)
result[t] = 255;
}
//
if (channels == 1) {
dst.at<uchar>(i - rowPadding, j - colPadding) = static_cast<uchar>(result[0]);
}
else if (channels == 3) {
Vec3b rgb;
rgb[0] = static_cast<uchar>(result[0]);
rgb[1] = static_cast<uchar>(result[1]);
rgb[2] = static_cast<uchar>(result[2]);
dst.at<Vec3b>(i - rowPadding, j - colPadding) = rgb;
}
}
}
}
void comparedAdaptiveMeanBlur(Mat& sapSrc, Mat& sSrc, Mat& pSrc, Mat& gSrc)
{
//3*3 的自适应均值滤波处理椒盐噪声
Mat dst1 = sapSrc.clone();
adaptiveMeanBlur(sapSrc, dst1, 3, 3);
imshow("3*3自适应均值滤波处理椒盐噪声结果", dst1);
//5*5 的自适应均值滤波处理椒噪声
Mat dst2 = pSrc.clone();
adaptiveMeanBlur(pSrc, dst2, 3, 3);
imshow("3*3自适应均值滤波处理椒噪声结果", dst2);
//3*3 的自适应均值滤波处理盐噪声
Mat dst3 = pSrc.clone();
adaptiveMeanBlur(sSrc, dst3, 3, 3);
imshow("3*3自适应均值滤波处理盐粒噪声结果", dst3);
//3*3 的自适应均值滤波处理高斯噪声
Mat dst4 = gSrc.clone();
adaptiveMeanBlur(gSrc, dst3, 3, 3);
imshow("3*3自适应均值滤波处理高斯噪声结果", dst4);
}
3.6.2 自适应局部降低噪声滤波实验效果
原图
添加噪声的图片,这里椒盐噪声、胡椒噪声、盐粒噪声比例为0.1， 高斯噪声 均值为15 方差为25。
3*3自适应局部降低噪声滤波
结果分析：这种方式的滤波，很适合处理高斯噪声。
7 自适应中值滤波器
前面使用中值滤波器对处理空间密度不大的脉冲噪声效果很好，但是当脉冲噪声的空间密度大时效果不佳。
所以这里有自适应中值滤波器来处理更大空间密度的脉冲噪声。
符号定义：
自适应中值滤波器以两个进程进行工作分别为进程A和进程B,如下方式：
进程A:
进程B:
7.1 自适应中值滤波编码实现
/*
* adaptive median filtering
* Anchor Point at top left corner
* S_Min =3,S_Max=5
* cyssmile
* 2020/3/19
*/
void adaptiveMedianBlur(Mat &images)
{
int S_Max = 5;
int S_Min = 3;
int row = images.rows;
int col = images.cols;
Mat images_clone = images.clone();
autoCopyMakeBorder(images, BORDER_DEFAULT, 1, S_Min);
vector<Mat> sub_images;
split(images,sub_images);
vector<Mat> sub_images_clone;
split(images_clone, sub_images_clone);
for (int i=0;i<images.channels();i++)
{
dealMainSplitImages(sub_images[i], sub_images_clone[i]);
}
Mat dst;
merge(sub_images_clone,dst);
dealDstEdges(dst, S_Max);
imshow("dst_output", dst);
}
/*
* get the min and max value in images
* cyssmile
* 2020/03/19
*/
void getMinMaxSplitChannel(Mat &images,double &min_val,double &max_val)
{
Point minloc, maxloc;
minMaxLoc(images, &min_val, &max_val, &minloc, &maxloc);
}
/*
* get the median value in images(roi)
* cyssmile
* 2020/03/19
*/
void getMedianSplitChannel(Mat &images,double &median_val)
{
vector<double> images_data;
for (int i =0;i<images.rows;i++)
{
for (int j = 0; j < images.cols; j++)
{
images_data.push_back(images.at<uchar>(i, j));
}
}
sort(images_data.begin(),images_data.end());
median_val = images_data[images.rows*images.cols/2];
}
/*
* process_B
* cyssmile
* 2020/03/19
*/
double process_B(double Z_xy,double min_val,double max_val,double median_val)
{
if (Z_xy-min_val>0 && Z_xy-max_val<0)
{
return Z_xy;
}
else
{
return median_val;
}
}
/*
* give a roi images and then return in (x,y) its (maybe) value
* cyssmile
* 20/03/19
*/
double dealSplitSubImages(Mat &split_images,int &S_now)
{
double min = split_images.at<uchar>(0, 0);
double &min_val = min;
double max = split_images.at<uchar>(0, 0);
double &max_val = max;
getMinMaxSplitChannel(split_images, min_val, max_val);
double median = split_images.at<uchar>(0, 0);
double &median_val = median;
getMedianSplitChannel(split_images, median_val);
double result_piexl= split_images.at<uchar>(0, 0);
if (median - min_val > 0 && median - max_val < 0)
{ // turn process B
result_piexl = process_B(split_images.at<uchar>(0, 0), min_val, max_val, median_val);
}else {
S_now = S_now + 2;
}
return result_piexl;
}
/*
* deal a splited channel images
* cyssmile
* 20/03/19
*/
void dealMainSplitImages(Mat &split_images,Mat &split_images_clone)
{
int S_Min = 3, S_Max = 7;
for (int i = 0; i < split_images_clone.rows; i++)
{
for (int j = 0; j < split_images_clone.cols; j++)
{
int S_now = S_Min;
double median;
double result_piexl = split_images_clone.at<uchar>(i, j);
if ((i + S_Max < split_images.rows )&& (j + S_Max < split_images.cols))
{
while (S_now <= S_Max)
{ //重复A处理过程
Rect rec;
rec.x = j;
rec.y = i;
rec.width = S_now;
rec.height = S_now;
if ((rec.x + S_now >= split_images.rows) && (rec.y + S_now >= split_images.cols))
{
break;
}
Mat sub = split_images(rec);
int S_old = S_now;
result_piexl = dealSplitSubImages(sub, S_now);
if (S_old == S_now)
{
break;
}
else
{
getMedianSplitChannel(sub, median);
result_piexl = median;
}
}
}
split_images_clone.at<uchar>(i, j) = result_piexl;
}
}
}
/*
* deal edges int dst images
* cyssmile
* 20/03/19
*/
void dealDstEdges(Mat &src,int edges)
{
Rect rec;
rec.x = src.cols - edges;
rec.y = 0 ;
rec.width = edges;
rec.height = src.rows;
Mat NeedDealMat = src(rec);
medianBlur(NeedDealMat, NeedDealMat, 3);
Rect rec_bottom;
rec_bottom.x = 0;
rec_bottom.y = src.rows - edges;
rec_bottom.width = src.cols;
rec_bottom.height = edges;
Mat NeedDealMat_bottom = src(rec_bottom);
medianBlur(NeedDealMat_bottom, NeedDealMat_bottom, 3);
}
7.2 自适应中值滤波处理效果
这里我选择的添加椒盐噪声的比例为0.25,前面的几个实验中添加的椒盐噪声比例只为0.1.
附
1、由于这次实验时间比较近，有很多细节没有完善好，有问题可以提醒我。
2、完整代码：https://github.com/cyssmile/openCV_learning_notes/tree/master/opencv_test/exercise9以上是关于在空域对图片加性噪声的去噪处理的主要内容，如果未能解决你的问题，请参考以下文章
图像去噪基于matlab GUI空域+频域滤波图像去噪含Matlab源码 029期