暑期集训第四天（6-25）题解及总结

Posted 2020-12-10 li-jia-hao

原本以为昨天老师考的已经够难了，弄了那么多的状压DP但是今天老师好像比昨天还狠，弄的状压题比昨天还多，还难，还额外弄了两道没做过的额外的题，还弄了两道tarjan......

 

 

 

 

 

 

 

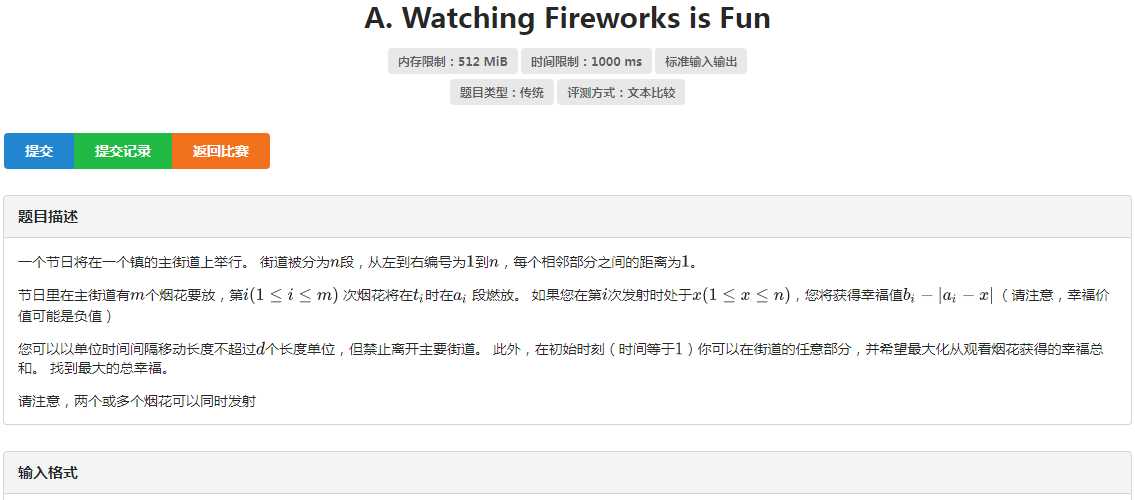
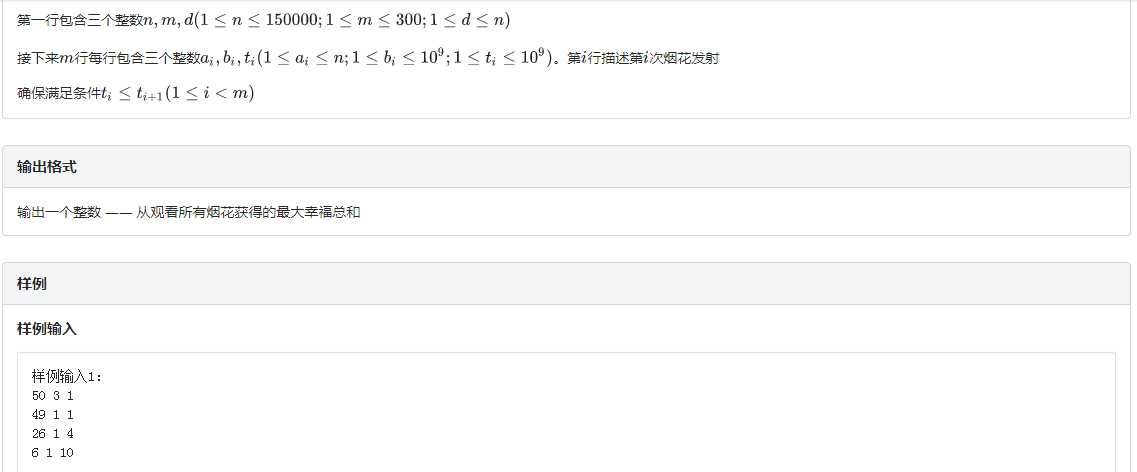
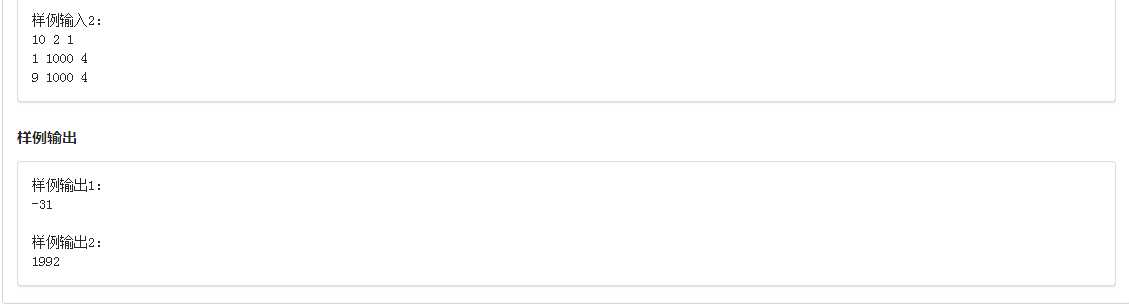
 这道题虽然是第一道题,但却是我最后改的(考试的时候没做出来),其实看完题解后觉得这道题也没有那么难,看来以后这类类似的对dp式子进行分析的题还要多做.

分析: 读完题目后考虑递推公式，dp[i][j]=max(dp[i-1][k])+b[i]-|a[i]-j|在这个式子之中b[i]的值是已经确定的，i一旦确定a[i]也就没有问题了，所以我们把目光聚焦在d[i][j]上我们当然可以用一个多重循环来解决这个问题，但是根据题目中的数据范围这样写是一定会超时的，但是假设我们最后站在j点，设h=(t1-t2)*d,那么我们的k的活动范围就在j+h和j-h之间,区间移动求一个最值,我们想到来使用单调队列来进行优化就可以了,dp如果硬开是开不下的,但是只和上一行的状态有关,所以用滚动数组优化.

 

 1 #include<cstring>
 2 #include<algorithm>
 3 #include<cstdio>
 4 #include<queue>
 5 typedef long long ll;
 6 using namespace std;
 7 const int maxn=15e4+5;
 8 ll dp[2][maxn];
 9 void Solve(){
10     int n,m,d;
11     scanf("%d%d%d",&n,&m,&d);
12     int t0=1,k=0; 
13     while(m--){
14         int a,t,b;
15         scanf("%d%d%d",&a,&b,&t);
16         ll h=(ll)1*(t-t0)*d;
17         h=min(h,(ll)n);
18         t0=t;
19         k=!k;
20         deque<int>q;//单调队列 
21         for(int i=1,j=1;i<=n;++i){
22             for(;j<=i+h&&j<=n;++j){
23                 while(!q.empty()&&dp[!k][q.back()]<=dp[!k][j]) q.pop_back();
24                 q.push_back(j);
25             }
26             while(!q.empty()&&q.front()<i-h) q.pop_front();
27             dp[k][i]=dp[!k][q.front()]+b-abs(a-i);
28         }
29     }
30     ll ans=dp[k][1];
31     for(int i=2;i<=n;++i)
32         ans=max(ans,dp[k][i]);
33     printf("%lld
",ans);
34 }
35 int main(){
36     //freopen("a.in","r",stdin);
37     Solve();
38     return 0;
39 }

Watching Fireworks is Fun

 

 

 

 

 

 

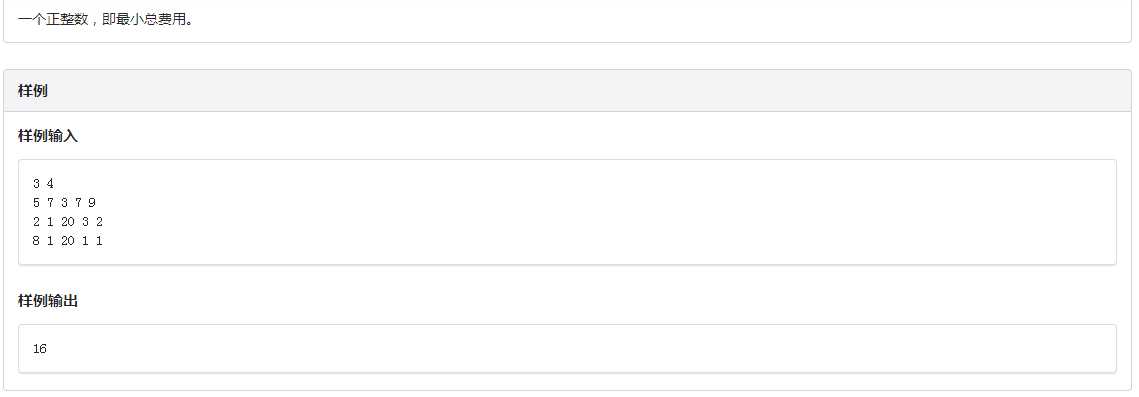
这道题在考场上不是没做出来,但是我写的dp太繁琐了,虽然只有三层循环,但是其中有两层是2^n级的,时间当然吃不住.

我们用dp[i][j]来表示在第i个店买了第j件物品的花费,在递推时考虑f[i][j]=min(f[i][j],f[i-1][j^(1<<(k-1))]+lf[i]+a[i][k]),其中lf表示路费,这个东西当然我们只在第一次进店时加一次就可以了,这样我们用三层循环n*m*2^n就可以求出最终的答案了，我当时考虑的是先把每个点每个状态都先预处理出来，最后再进行dp，导致在进行转移时十分麻烦，转移方程还是十分重要的呀。

 1 #include<map>
 2 #include<stack>
 3 #include<cstdio>
 4 #include<cstring>
 5 #include<algorithm>
 6 const int N=5e2+10;
 7 using namespace std;
 8 #define debug printf("-debug-
")
 9 struct Node{
10     int dis,next,to;
11 }edge[N];
12 int Head[N],tot;
13 int dian[N][20];
14 int dp[N][1<<17],f[2][1<<17];
15 signed main(){
16     //freopen("a.in","r",stdin);
17     //freopen("a.out","w",stdout);
18     int n,m;
19     scanf("%d%d",&n,&m);
20     int t=(1<<(m))-1;
21     for(int i=1;i<=n;++i){
22         scanf("%d",&dian[i][0]);
23         for(int j=1;j<=m;++j){
24             scanf("%d",&dian[i][j]);
25         }
26     }
27     for(int i=1;i<=n;++i)
28         for(int j=0;j<=t;++j){
29             dp[i][j]+=dian[i][0];
30             for(int k=0;(j>>k)>0;++k){
31                 if((j>>k)&1) dp[i][j]+=dian[i][k+1];
32             }
33         }
34     memset(f,0x3f,sizeof(f));
35     f[0][0]=f[1][0]=0;
36     int p=0;
37     for(int i=1;i<=n;++i){
38         p=!p;
39         for(int j=0;j<=t;++j)
40             for(int k=0;k<=t;++k){
41                 f[p][j]=min(f[p][j],f[!p][j]);
42                 f[p][j|k]=min(f[p][j|k],f[!p][j|k]);
43                 f[p][j|k]=min(f[p][j|k],f[!p][j]+dp[i][k]);
44                 //printf("%d
",f[][j|k]);
45             }
46     }
47     printf("%d
",f[p][t]);
48     return 0;
49 }

蒟蒻的超时代码

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 ll f[105][1<<17],a[105][105],lf[105];
 5 int main(){
 6     memset(f,0x3f,sizeof(f));
 7     int n,m;
 8     scanf("%d%d",&n,&m);
 9     for(int i=1;i<=n;i++){
10         f[i][0]=0;
11         scanf("%lld",&lf[i]);
12         for(int j=1;j<=m;j++){
13             scanf("%lld",&a[i][j]);
14         }
15     }
16     int mmax=(1<<m)-1;
17     f[0][0]=1;
18     for(int i=1;i<=n;i++){
19         for(int j=0;j<=mmax;j++){
20             for(int k=1;k<=m;k++){
21                 if(j&(1<<(k-1))){
22                     if(i>=2) f[i][j]=min(f[i][j],f[i-1][j^(1<<(k-1))]+lf[i]+a[i][k]);
23                     if((j^(1<<(k-1)))==0) f[i][j]=min(f[i][j],lf[i]+a[i][k]);
24                     else f[i][j]=min(f[i][j],f[i][j^(1<<(k-1))]+a[i][k]);
25                 }
26             }
27         }
28         for(int j=0;j<=mmax;j++){
29             f[i][j]=min(f[i][j],f[i-1][j]);
30         }
31     }
32     printf("%lld
",f[n][mmax]);
33     return 0;
34 }

The Prices

 

 

 

 

 

 

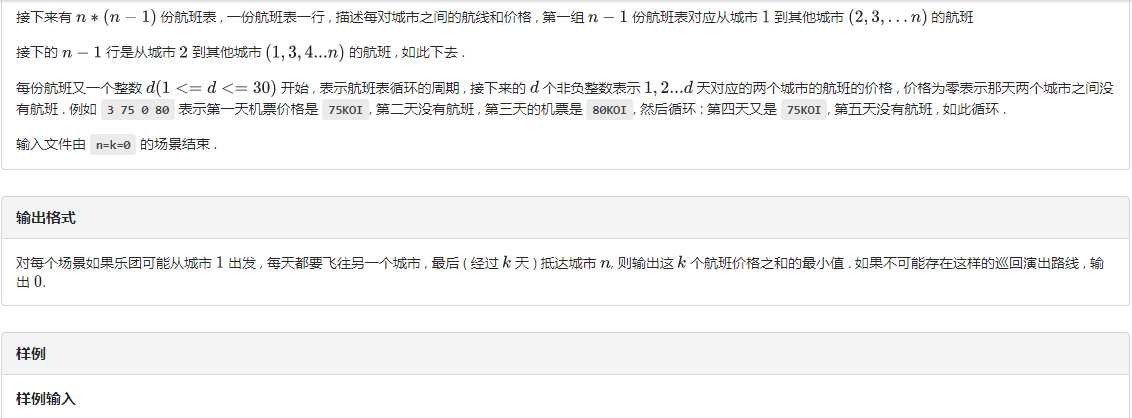
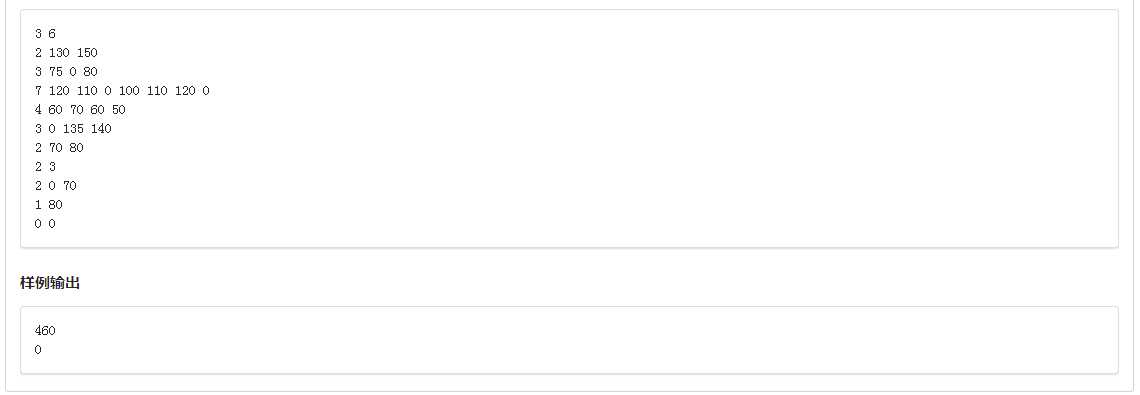
 这道破题让我调了一下午，周围的人都看了题解也不知道我错在了那里，之后向大佬请教才知道是题意理解错了（明明是它说的不清），我的方法调出来之后和别人对比后发现时间大概比别人多跑了30倍，内存多了20倍.......

考虑dp[i][j][k]表示第i天最后在j地时的状态为k时的答案,于是有转移方程:dp[i][v][k|(1<<(v-1))]=min(dp[i][v][k|(1<<(v-1))],dp[i-1][u][k]+cost[u][v][D]);(其中的u表示出发点,v表示到达点),四层循环枚举i,u,v,k(看起来就很麻烦对不对?我也这么觉得,难怪它跑得这么慢),之后枚举dp[m][n]的第三维求出最小值就可以了,需要注意的几点:天数要取模是当然的,但是取完模后数可能变成0,输出会变为一句话:浮点数除外,另外,if语句能少写就少写把,在你调代码时你会感谢你自己的.

 1 #include<map>
 2 #include<stack>
 3 #include<cstdio>
 4 #include<cstring>
 5 #include<algorithm>
 6 #include<iostream>
 7 const int N=5e2+10;
 8 using namespace std;
 9 typedef long long ll;
10 #define debug printf("-debug-
")
11 int count(ll x){
12     int cnt=0;
13     while(x){
14         if(x & 1) cnt++;
15         x>>=1;
16     }
17     return cnt;
18 }
19 ll dp[1001][11][1<<10];
20 int cost[11][11][1001];
21 int main(){
22     //freopen("a.in","r",stdin);
23     //freopen("a.out","w",stdout);
24     int n,m;
25     while(scanf("%d%d",&n,&m)==2 && n && m){
26         for(int i=1;i<=n;++i)
27             for(int j=1;j<=n;++j){
28                 if(i==j) continue;
29                 scanf("%d",&cost[i][j][0]);
30                 for(int k=1;k<=cost[i][j][0];++k){
31                     scanf("%d",&cost[i][j][k]);
32                     //printf("%d %d %d %d
",i,j,k,cost[i][j][k]);
33                 }
34             }
35         memset(dp,0x3f,sizeof(dp));
36         dp[0][1][1]=0;
37         int t=(1<<n)-1;
38         for(int i=1;i<=m;++i)
39             for(int u=1;u<=n;++u)
40                 for(int v=1;v<=n;++v)
41                     for(int k=0;k<=t;++k){
42                         if(!(k&(1<<(u-1)))) continue;
43                         if(v==u) continue;
44                         int D=(i+cost[u][v][0])%cost[u][v][0];
45                         if(D==0) D=cost[u][v][0];
46                         if(!cost[u][v][D]) continue;
47                         dp[i][v][k|(1<<(v-1))]=min(dp[i][v][k|(1<<(v-1))],dp[i-1][u][k]+cost[u][v][D]);
48                     }
49         ll ans=0x3f3f3f3f3f3f3f3f;
50         for(int i=0;i<=t;++i)
51             ans=min(ans,dp[m][n][i]);
52         if(ans==0x3f3f3f3f3f3f3f3f){
53             printf("0
");
54             continue;
55         }
56         else printf("%lld
",ans);
57     }
58     return 0;
59 }

Perform巡回演出

 

 

 

 

 

 

(篇幅限制删去了一些图)

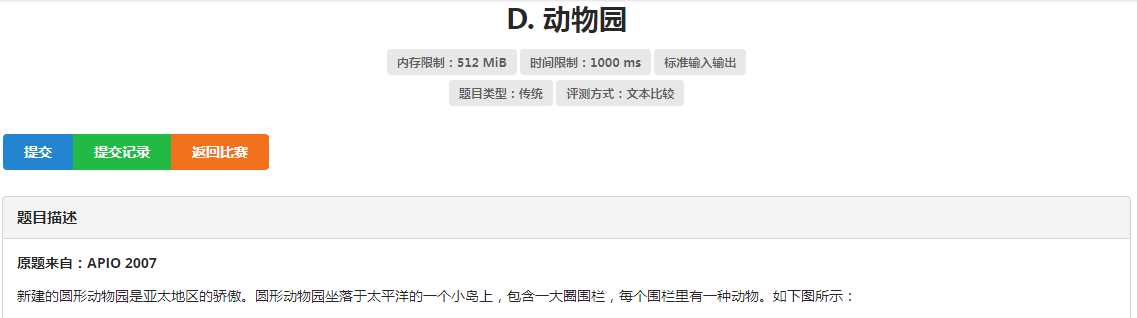
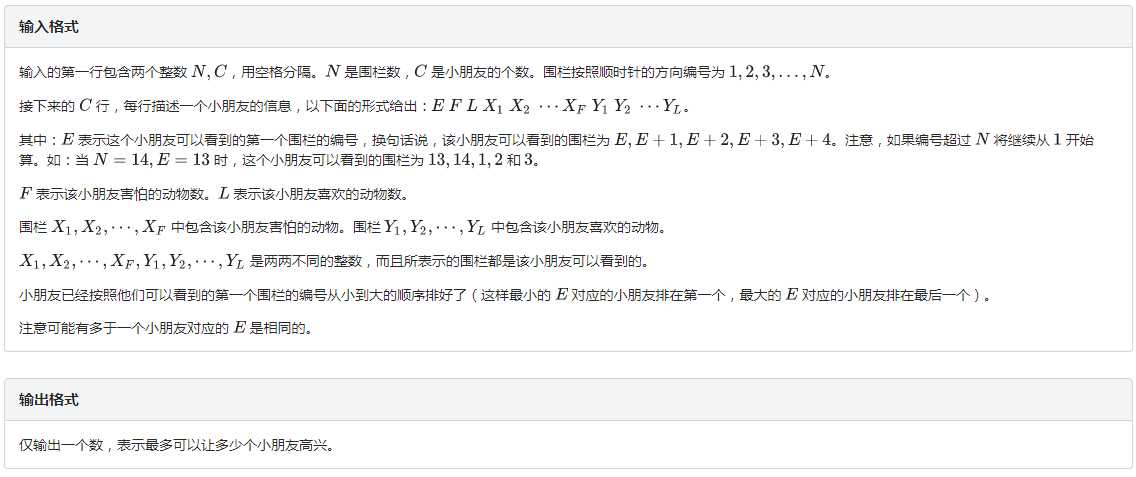
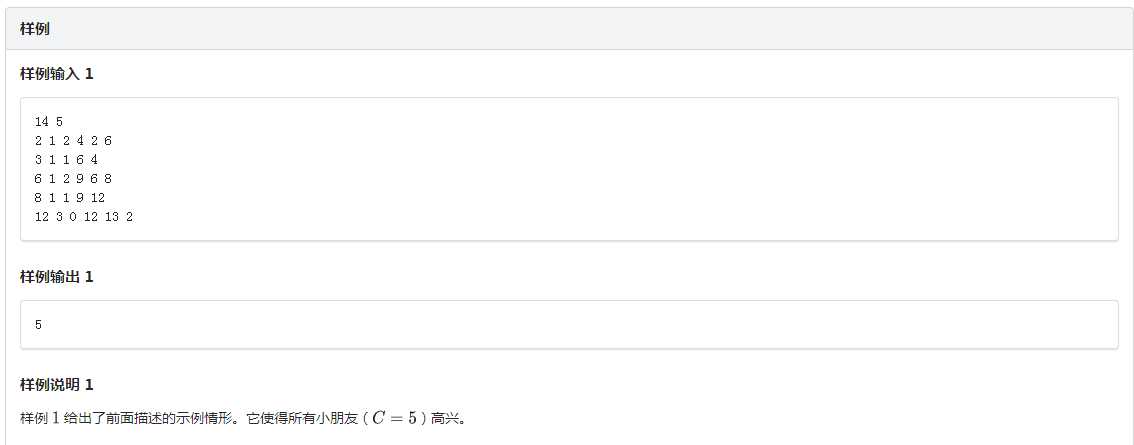
其实这是挺久远的一道题了,这也是我集训以来第一道首A的题(我才不会说是因为提前复习了).

考虑现将每一个小盆友的喜欢和讨厌的状态转化到num数组上,来表示对应字母开头的状态的可以让小盆友满意的人数,这道题的核心部分我认为是在dp的部分,我们有dp[k][j]=max(dp[k-1][(j&15)<<1],dp[k-1][(j&15)<<1|1])+num[k][j];通过&15的计算我们可以取出上一状态的四位数,再对第五位来进行决策,即该位是否为1,在加上之前处理出的num数组,就可以完成这道题的转移了,另外由于这道题的起始状态不好进行确定,那就都试一遍就行了,注意每次实验的初始化和答案比较.

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 const int N=1e5+10;
 5 using namespace std;
 6 int num[N][35],dp[N][35];
 7 int main(){
 8     int n,m;
 9     scanf("%d%d",&n,&m);
10     for(int i=1;i<=m;++i){
11         int a,b,c;
12         int fear=0,like=0;
13         scanf("%d%d%d",&a,&b,&c);
14         while(b--){
15             int x;
16             scanf("%d",&x);
17             fear|=(1<<((x-a+n)%n));
18         }
19         while(c--){
20             int x;
21             scanf("%d",&x);
22             like|=(1<<((x-a+n)%n));
23         }
24         for(int j=0;j<32;++j)
25             if((j&fear)||(~j&like)) num[a][j]++;
26     }
27     int ans=0;
28     for(int i=0;i<32;++i){
29         memset(dp[0],128,sizeof(dp[0]));
30         dp[0][i]=0;
31         for(int k=1;k<=n;++k)
32             for(int j=0;j<32;++j)
33                 dp[k][j]=max(dp[k-1][(j&15)<<1],dp[k-1][(j&15)<<1|1])+num[k][j];
34         ans=max(ans,dp[n][i]);
35     }
36     printf("%d
",ans);
37     return 0;
38 }

动物园

 

 

 

 

 

 

 

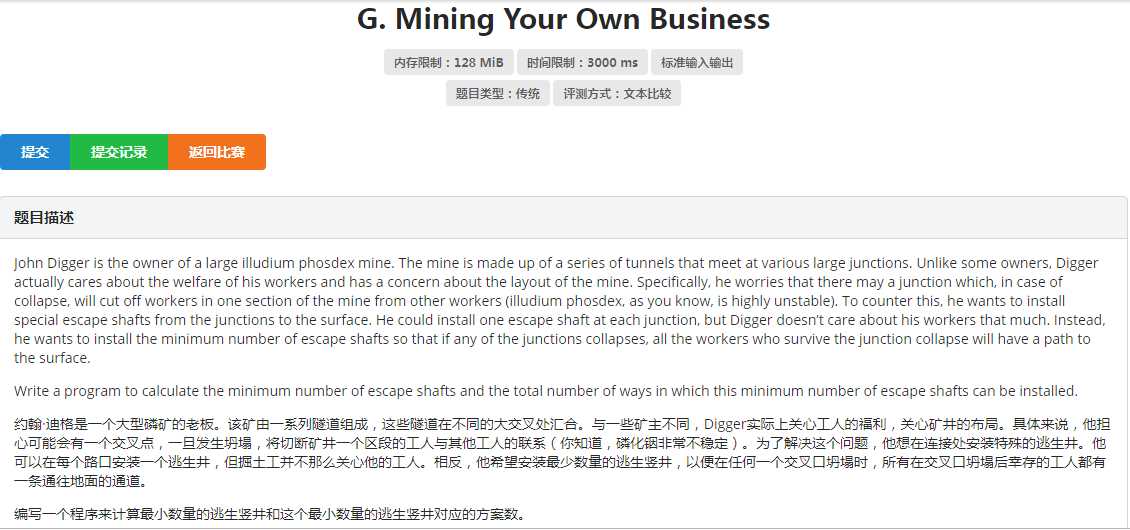
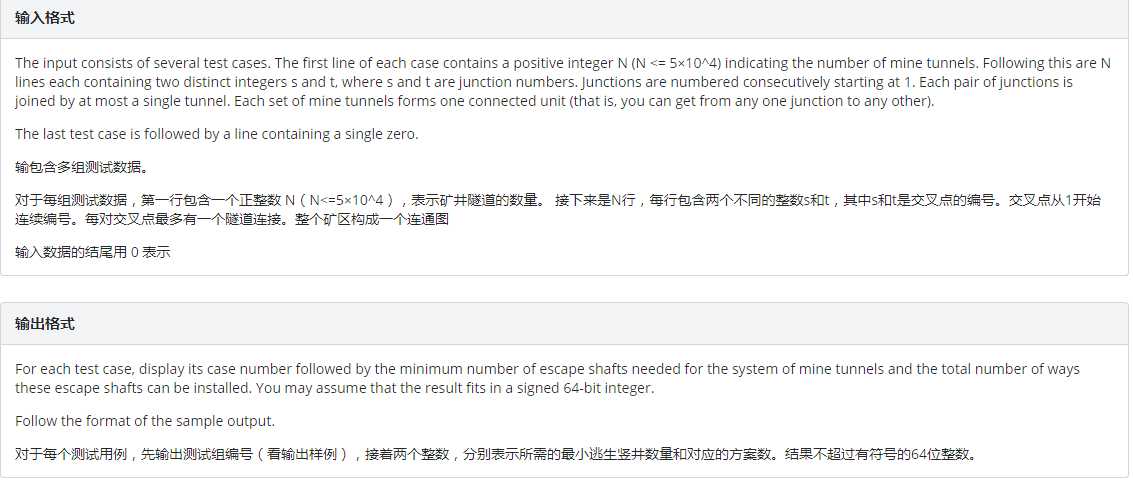
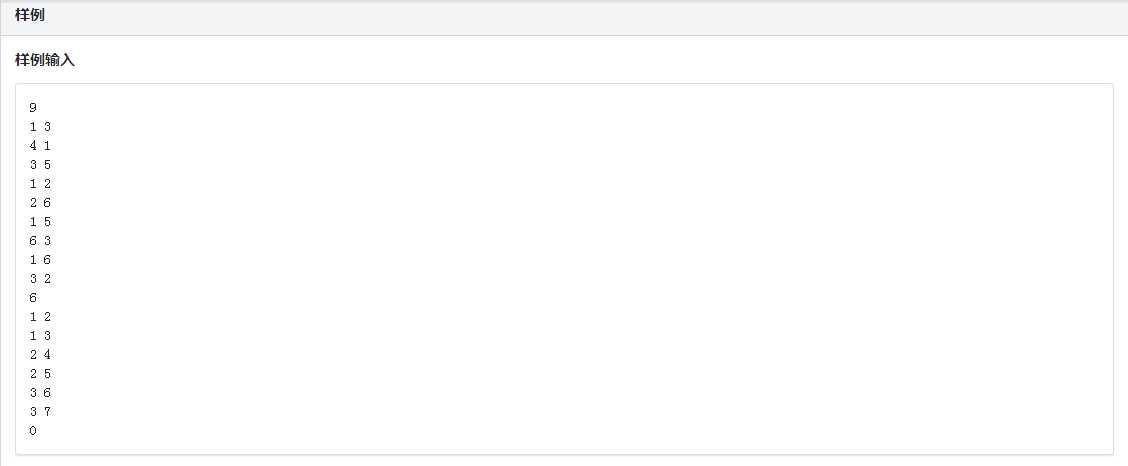
 我原本以为老姚和虎哥都挺和善的,最近出的tarjan的题也都不怎么难,直到我看见了这道题,也理解了他们是真的‘核‘善.

记得刚学完tarjan的时候这是lc大佬Wa的次数最多的一道题,每次我进入题库都能看见他的记录:听取WA声一片(lc大佬:我没有,你瞎说).

想做这道题会写tarjan的板子是最基础的,之后才能来进行考虑之后的处理,我们考虑,如果这个图之中没有割点,那么我们只要去开设两个点就行了,因为开一个点万一这个点塌了点就废了,答案为2和n*(n-1)/2，我们主要处理的应该是有数个割点的情况，我们把一张图分为几个联通块来处理，如果一个带有数个割点的联通块的一个割点塌了，里面的工人还可以跑到其他联通块，所以里面不用设点，关键就是只有一个割点缩完点在外面吊着的联通块，割点塌了里面的人就出不来了，所以必须在这里面进行设点，答案贡献是乘以bcc[i].size()-1，第一个答案的值就是在外面吊着的联通快的个数，这样这道题就解决了。

 1 #include<cstdio>
 2 #include<algorithm>
 3 #include<stack>
 4 #include<vector>
 5 #include<cstring>
 6 using namespace std;
 7 #define int long long
 8 const int N=1e6+10;
 9 struct Node{
10     int next,to;
11 }edge[N];
12 int Head[N],tot;
13 void Add(int x,int y){
14     edge[++tot].to=y;
15     edge[tot].next=Head[x];
16     Head[x]=tot;
17 }
18 stack<int>sta;
19 vector<int>bcc[N];
20 int dfn[N],low[N],dfn_cnt,bcc_cnt,cut[N];
21 void tarjan(int u){
22     dfn[u]=low[u]=++dfn_cnt;
23     sta.push(u);int flag=0;
24     for(int i=Head[u];i;i=edge[i].next){
25         int v=edge[i].to;
26         if(!dfn[v]){
27             tarjan(v);flag++;
28             low[u]=min(low[u],low[v]);
29             if(low[v]>=dfn[u]){
30                 bcc_cnt++;bcc[bcc_cnt].clear();
31                 int t;
32                 do{
33                     t=sta.top();sta.pop();
34                     bcc[bcc_cnt].push_back(t);
35                 }while(t!=v);
36                 bcc[bcc_cnt].push_back(u);
37                 if(u!=1||flag>1) cut[u]=1;
38             }
39         }
40         else low[u]=min(low[u],dfn[v]);
41     }
42 }
43 signed main(){
44     //freopen("a.in","r",stdin);
45     int m,Case=0;
46     while(scanf("%lld",&m)==1 && m){
47         printf("Case %lld: ",++Case);
48         memset(Head,0,sizeof(Head)); tot=0; 
49         memset(cut,0,sizeof(cut));bcc_cnt=0;dfn_cnt=0;
50         memset(low,0,sizeof(low));
51         memset(dfn,0,sizeof(dfn));
52         int n=0;
53         memset(cut,0,sizeof(cut));
54         for(int i=1;i<=m;++i){
55             int x,y;
56             scanf("%lld%lld",&x,&y);
57             n=max(n,max(x,y));
58             Add(x,y);Add(y,x);
59         }
60         for(int i=1;i<=n;++i)
61             if(!dfn[i]) tarjan(i);
62         int ans1=0,ans2=1;
63         if(bcc_cnt==1){
64             ans1=2;
65             ans2=n*(n-1)/2;
66         }
67         else{
68             for(int i=1;i<=bcc_cnt;++i){
69                 int cnt=0;
70                 for(int j=0;j<bcc[i].size();++j){
71                     if(cut[bcc[i][j]]) cnt++;
72                 }
73                 if(cnt==1){
74                     ans1++;ans2*=(bcc[i].size()-1);
75                 };
76             }
77         }
78         printf("%lld %lld
",ans1,ans2);
79     }
80 }

Mining Your Own Business

总结：  其实今天还是可以的，但是值得反思的地方还有很多，比如今天下午我感觉效率就十分低下，一道现在看来不难的题硬是调了一个下午，老姚说的想好再交我还是没有落实好呀，此外，在今天晚上做额外的题时候还是会忍不住看题解，以后可以尝试去一些没有题解的题库网站来严格要求一下自己，比如在做内部题库时我就没想过看题解，在洛谷时那个题解按钮特别吸引人，以后我会严格要求自己的