考研线性代数

Posted 2020-12-10 xxhao

行列式

行列式就是一个数或者一个式子

定义

• 逆序： 若(i<j - (i,j))称为正序，若(i>j - (i,j))称为逆序
• 逆序数：一个排列里面包括的逆序的总个数
• n阶行列式：n阶行列式等于所有取自不同行不同列的n个元素的乘积的代数和，逆序数为偶数时带正号，逆序数为奇数时带负号，共有n!项
• 余子式：行列式划去该元素所在的行与列的各元素,剩下的元素按原样排列,得到的新行列式
• 代数余子式：行列式某元素的余子式与该元素对应的正负符号的乘积
• (A_{ij}=(-1)^{(i+j)}M_{ij}) 其中 (A_{ij})为代数余子式，(M_{ij})为余子式

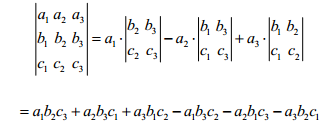
易算行列式

• 对角行列式：上三角，下三角，对角都为主对角线乘积
• 范德蒙行列式

[V_n= left[ egin{matrix} 1 & 1 & cdots & 1 a_1 & a_2 & cdots & a_n a^2_1 & a^2_2 & cdots & a^2_n vdots & vdots & ddots & vdots a^{n-1}_1 & a^{n-1}_2 & cdots & a^{n-1}_n \end{matrix} ight]=prod_{1leq j<ileq n}(a_i-a_j) ]

(V_n!=0) 充分必要 (a_1,a_2,a_3 cdots a_n)两两不等

计算性质

• 行列式与其转化行列式相等，即(D=D^T)
• 对调两行或者两列改变符号
• 行列式某行（或列）有公因子可以提取到行列式的外面
• 若行列式某行（或列）元素全为零，则该行列式值为零
• 若行列式某两行（或列）元素相同或者成比例，则该行列式值为零

[left[ egin{matrix} a_1+b_1 & c_1 a_2+b_2 & c_2 \end{matrix} ight] = left[ egin{matrix} a_1 & c_1 a_2 & c_2 \end{matrix} ight] + left[ egin{matrix} b_1 & c_1 _2 & c_2 \end{matrix} ight] ]

[left[ egin{matrix} a_{11} & a_{12} & cdots & a_{1n} \vdots & vdots & ddots & vdots a_{i1} & a_{i2} & cdots & a_{in} \vdots & vdots & ddots & vdots a_{j1} & a_{j2} & cdots & a_{jn} \vdots & vdots & ddots & vdots a_{n1} & a_{n2} & cdots & a_{nn} \end{matrix} ight]= left[ egin{matrix} a_{11} & a_{12} & cdots & a_{1n} \vdots & vdots & ddots & vdots a_{i1} & a_{i2} & cdots & a_{in} \vdots & vdots & ddots & vdots a_{j1}+ka_{i1} & a_{j2}+ka_{i2} & cdots & a_{jn}+ka_{in} \vdots & vdots & ddots & vdots a_{n1} & a_{n2} & cdots & a_{nn} \end{matrix} ight] ]

矩阵

向量

线性方程组

矩阵的特征值和特征向量

二次型