6.2符号的模拟——算术

Posted 2020-12-10 character2

6数学与计算

6.1语句与公式

6.2符号的模拟——算术

从历史与逻辑二方面考察，算术——自然数的理论是的基础。今天看来很简单的算术，历史上经历过数千年的发展才成为今天的样式。人类个体学习经历也与此对应，每个正常人从呀呀学语时就开始接触到数数，之后经历过漫长的幼儿园与小学的学习，也是长达近十年的时间我们才算掌握了算术。算术原理上说很简单：就是后续的关系，再加数学完全归纳法，更完整的说法是意大利数学家皮亚诺（peano）的算术公理系统：

1、0是自然数

2、每一个确定的自然数n，都有一个称为n的后继数s（n）的自然数

3、0不是任何自然数的后继

4、任意二个不同的自然数不能有相同的后继数

5、对于命题P(n)，如果下面二个判断同时成立

    P（0）=1

    P(n)=1⇒P(s（n）)=1

    那么∀n∈N，P(n)=1（N为自然数集）

上面是自然语言的陈述，其中第5公理就是数学的完全归纳法。本书在其它位置讲到算术时，为了特定表述的简单，自然数是从1开始而不是从0开始。皮亚诺的工作不仅是整理出算术公理，而且最大程度地实现了希尔伯特倡导的形式化，即不依靠自然词汇，由抽象符号组成系统。不过这不是这里要讲的。算术漫长历史上，关键的进展并不是明白这些原理。

算术之前，早期人类要对事物计数，比如一个牧羊人要对其放牧羊群的数量有所掌握，他可以这样做：早上从羊圈里每放出一只羊，就在羊圈门口的特定位置放置一个石子，所有羊从羊圈出来后所堆成的石堆就是自己羊群的数量，妥善地保管这个石堆；每天晚上放牧回来时，每有一只羊进入羊圈时，就可以从早上的石堆拿开一个石子，最后一只羊进圈时正好拿开石堆的最后一个石子，说明今天的羊没有丢失，也没有其它牧羊人的羊混进自己的羊群或者进出羊的数量相等。石子计数的方法可进一步发展，比如可以匹配二堆石子来比较二群羊数量熟多熟少，或者羊群比猪群数量多出多少。这些方法足够让人满意，自然人们会去寻找如小鹅卵石那样方便操作、易于保管、甚至让人喜欢的石子作为这里的工具，还可以制作羊皮袋，专门用于收纳石子。如果牧羊人第二年改为牧牛了，他也仍会先尝试石子来对牛记数。这不是完全虚拟的描述，英文中的计算为“Calculation”，来自拉丁文中的“Calculus”，指的是计算用的小石头。

通常认为数的抽象是算术发展上的一个难点，考察自然语言，3只羊与3头牛，或3 匹马通常是不同的数量词。数的抽象性对心智是个挑战，对抽象性的克服更可能是实践上不同物品计数可以是相同操作：拿来拿去石子；在木头上一道道地刻痕；在绳子上打结。这些操作的适用性最终让心智顺应了数的抽象性，不太可能是其它方式上导致意识上的突进。

小鹅卵石、小木棍等可视为后来的数字。它们都是一种中介物，对这种中介物的操作帮助我们从数量上掌握实际的事物。鹅卵石对羊群的计数，只是一种离散事物对另一种离散事物的模拟操作，在这里鹅卵石与羊群相比，只是具有更容易为我们人类掌管与操作的性质。二个大小差不多，数量相近的石堆，只是看到它们，我们并不能意识到各是多少，谁多谁少，但它们的性质可以让我们去做匹配操作，区分出谁多谁少。

我们考察下古代书写1、2、3、4、5…这些数字的符号。

 

中文里它们是这样写的：

一、二、三、四、五

更早的写法是：

  

古玛雅文明里1-4就分别是对应数量的圆点来表示，5很可能是5个点，后面演化成了一条线。其它的古代文明大致都是这样的写法。从数的表示符号推测：历史上人类可能首先是尝试一进制的数字表示，这可能是源自实物记数。一进制的数字，它都不是象形字，它就是纸面上鹅卵石，另一种形式的离散事物，只是它是完全人造的，表示于某一平面，且操作上会与鹅卵石不一样：主要是书写与擦除的操作。加法、减法的原型很可能就是拿过来拿过去这样的动作或类似的动作，在古代埃及的符号表示中，就是用人脚走近、走远的象形文字表示加法与减法的。

真正成为符号，一进制并不是好主意。符号系统的一个要求是要制造更明显的区别来产生分立以表征对应内容上的差异，一进制在符号的辨别上没有什么技巧，数字稍微大些，辨识与书写就变得同样不可能。从一进制到多进制，确立多进制的位置记数法，是算术发展历史上决定性的步骤。因为人类有二只手十个指头，十进制位置记数法最终为全人类通用。如果说是一进制方法用于计数、计算是一种离散事物对别的离散事物的模拟操作，十进制位置记数法同样如此，一进制与其它的进制原理上并无改变，改变的是形式，形式的变化是整体性的协变，不同进制的位置记数法是等效的。

从一进制到十进制，辨识上通过位置记数法的技巧得到了改进。首先是个位数上采用了阿拉伯数字，关于阿拉伯数字，另一说法是印度人最先使用的。大于9的数字，通过数字、位置、进位有规则地表示或区分，这使得任意大数值表示不再是个问题。多进制的位置记数法也使得自然数的四则运算也都可以建立简单的规则，遵循这些规则进行机械的操作，我们就可以完成自然数范围内任何复杂的四则运算。

从一进制到多进制，只是加入了一些技巧，让数的表示与识别更容易。同时，所发生的屈折的变化，减弱了原有的直观性，带来理解掌握上的复杂度。在一进制下，加法就是连接起来就可以，十进制下就需要掌握加法表与进位法，位置在一进制里都是同样的，在多进制里，不同位置是不同的“阶”。这种“屈折变化”是数学上常见的方式，比如把连加的计算表示为乘法，这让数学有了不同的等效形式，便于数学本身的衍生，同时让数学变得复杂抽象。

皮亚诺（peano）的算术公理系统并没有刻画位置记数法的实现机制，反过来，位置记数法包含了后续概念，但没有包括完全归纳法外。皮亚诺（peano）的算术公理系统是纯逻辑的，它是理论基础上的研究。实用上位置记数法才是支撑的机制。这是有区别的二个方向，公理化方法可以梳理逻辑的前提与依赖关系，使系统得以完善。位置记数法更多是技巧面的，它们让系统变得实用、适用。从历史与实践来说，算术的成功，不是抽象思维，不是逻辑整理上的成功，而是作为工具构想上的成功。

十进制的采用，让人类可以搬手指与应用如手肘这样的身体部位来计数，这是小学生常见的动作，也是很多人一生离不开的动作。一进制来源于对实物计数的模拟，实物计数是以搬来搬去的动作为基础的，反映于符号上，自然数的后继概念也是以“+1”计算为基础。手指上的计数动作或对实物操作的计数动作，也可以在心理上拟想，简单的计算，我们可以通过心算来进行。一个启发性的观点是：数学上的深层机制是操作，这包括了对实际对象的操作，符号上对实际操作的模拟，以及内化为心理上动作。三个层面相互可转化可能构成理解的基础，而且转化没有固定的方向，实数概念可能先来自心理上分割动作，然后外化为符号上的操作。

我们再来看后续数学的发展，这首先是计算方式的扩展，从四则运算，到平方、开方、指数、对数的运算，微分、积分的运算……。对应着数系的扩展，并不是人们实际观察到不同类型的数，而是为了让算术运算、代数运算及其它的运算能够闭合，使运算法法则具有普遍性而不断构造出的。为了减法运算的施行构造了负数，为了除法运算的施行构造了分数，为了开方运算的施行构造了无理数、虚数，其中虚数是求负数的平方根时引入的，后面继续构造了复数、四元数等。在这种构建中，计算操作与初始符号同时出现，后续符号可看作计算生成，符号间的关系也可计算来定义。

 

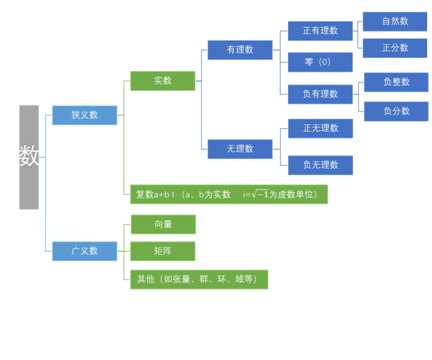
继续这个方向的讨论，会遇到无限产生的难题。对于实数集而言，不可计算甚至不能表示——不包括专名表示—的实数，如各种超越数，实际多于我们熟悉的那些实数，这样大于、小于、极限、无限的阶等这些概念成为基础分析上需要依赖的概念。

（作者（LQS）注：连续地阅读会发现，系列的文章不是对各个问题的解释，而是新的理解视角）