树状数组

Posted 2020-12-09 spciay

目录

• 树状数组
  • 1. 算法分析
  • 2. 板子
    • 2.1 单点修改+区间查询
    • 2.2 区间修改+单点查询
    • 2.3 区间修改+区间查询
  • 3. 例题

树状数组

1. 算法分析

树状数组作用

1. 单点修改
2. 区间查询
3. 区间修改(加上差分)
   

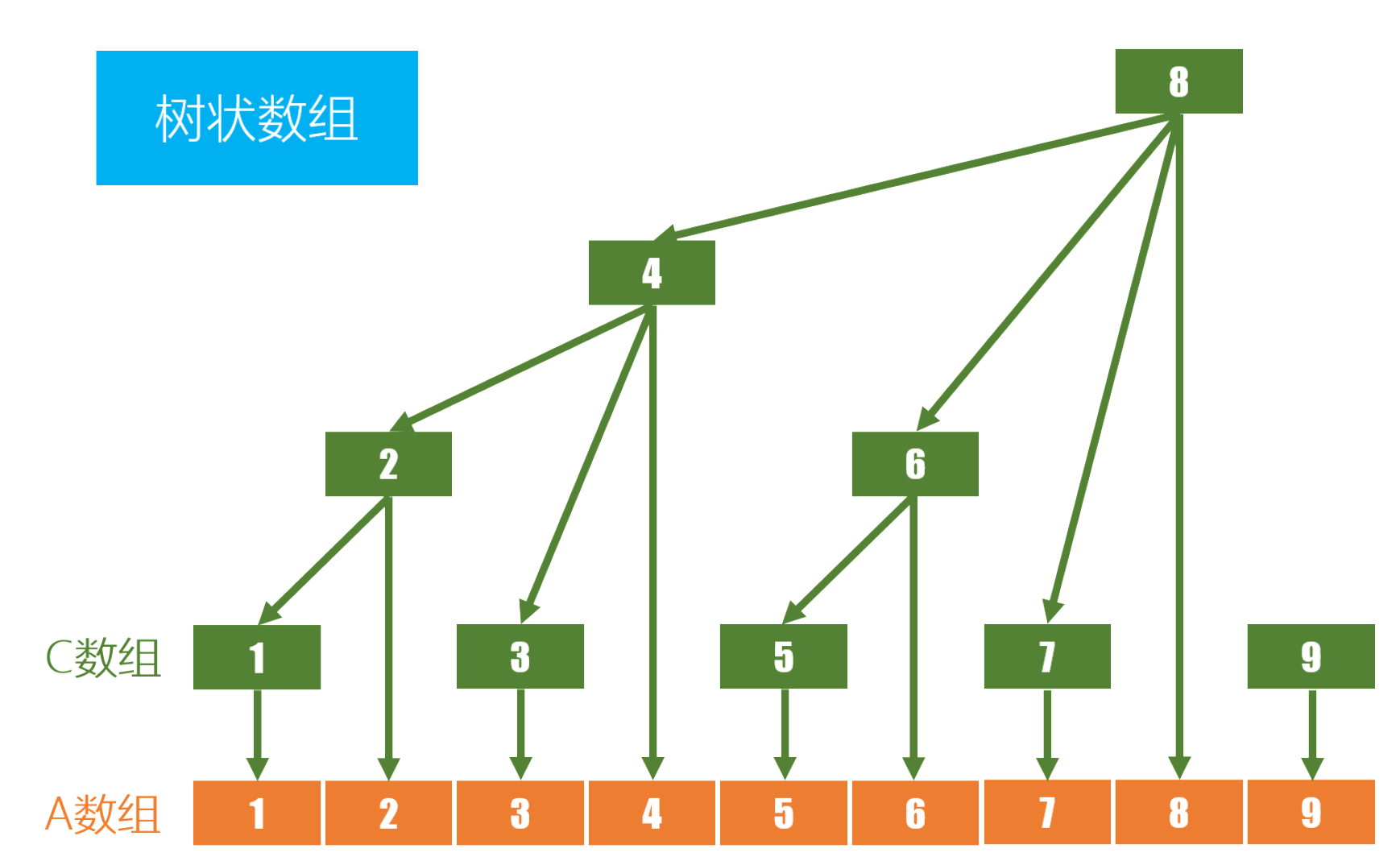
核心思想
????把前n个数划分为log(n)个区间，分别维护这log(n)个区间的和，在求解前缀和S_n的时候，从求解n个数字的和变成求解log(n)个区间的和来加快运算

具体操作
????维护log(n)个区间，每个区间用数组c来维护区间和。单点修改x的时候，修改x所在的c，然后一路向上修改父节点的c；区间查询[1 ~ x]的时候，从x开始向前，把x的所有兄弟节点的c都加起来

c数组性质

1. c[x]数组维护区间[x - lowbit(x) + 1, x]的和
2. c[x]数组维护的区间的长度为lowbit(x)
3. c[x]的父节点为 c[x + lowbit(x)]
4. c[x]前一个兄弟节点为 c[x - lowbit(x)]

2. 板子

2.1 单点修改+区间查询

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
int const N = 5e5 + 10;
int a[N], n, m;
LL c[N], sum[N];  // c[x] = a[x-lowbit(x) + 1] + ... + a[x]，sum[x]=a[1]+...+a[x]

int lowbit(int x) {
    return x & (-x);
}

// 单点修改
void add(int x, int y) {
    for (int i = x; i <= n; i += lowbit(i)) c[i] += y;  // 不断往父节点跳
}

// 查询Sx前缀和
LL query(int x) {
    LL res = 0;
    for (int i = x; i; i -= lowbit(i)) res += c[i];  // 不断往前一个兄弟节点跳
    return res;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);  // 读入每个元素
        sum[i] = sum[i - 1] + a[i];  // 计算前缀和
    }
    
    for (int i = 1; i <= n; ++i) c[i] = sum[i] - sum[i - lowbit(i)];  // 初始化c数组
    
    for (int i = 1, op, x, y; i <= m; ++i) {  // m个操作
        scanf("%d%d%d", &op, &x, &y);  
        if (op == 1) add(x, y);   // 单点修改
        else printf("%lld
", query(y) - query(x - 1));  // 区间查询
    }
    
    return 0;
}

2.2 区间修改+单点查询

/*
本题要进行的是 区间增加+单点询问，而树状数组能进行的操作为 单点增加 + 区间查询
可以通过差分来实现这个转变，使得树状数组可以完成区间增加 + 单点询问
即：维护一个b数组表示当前a数组的增加减少情况，一旦a数组[l, r]增加d， 那么b[l] += d, b[r + 1] -= d
因此我们可以用树状数组维护这个b数组的前缀和，即维护一个c数组，记录b数组的前缀和，那么通过add()操作就能改变前缀和
而后每次询问单点时，我们查询b数组的前缀和就可以知道a点的增加减少情况
*/


#include<bits/stdc++.h>
using namespace std;

typedef long long LL;

int n, m;
int const N = 1e5 + 10;
int c[N], a[N];  // c[x]维护的是b数组的前缀和

int lowbit(int x) {
    return x & -x;
}

// 单点修改
void add(int x, int y) {
    for (int i = x; i <= n; i += lowbit(i)) c[i] += y;  // 不断往父节点跳
}

// 查询Sx前缀和
LL query(int x) {
    LL res = 0;
    for (int i = x; i; i -= lowbit(i)) res += c[i];  // 不断往前一个兄弟节点跳
    return res;
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);  // 读入a[i]
    while (m--) {
        string op;
        int l, r, d, x;
        cin >> op;

        // 单点查询
        if (op[0] == ‘Q‘) {
            scanf("%d", &x);
            printf("%lld
", query(x) + a[x]);  // x点的变化值+a[x]
        }
        else {
            scanf("%d %d %d", &l, &r, &d);
            add(l, d), add(r + 1, -d);  // 区间增加
        }
    }
    return 0;
}

2.3 区间修改+区间查询

/*
对于第一种处理方式，可以利用差分结合acwing242一个简单的整数问题1的方式来处理；
对于问题而求区间和，那么考虑维护a的前缀和
a1+a2+...+ax=(b1)+(b1+b2)+(b1+b2+b3)+...+(b1+b2+b3+..+bx)
=(1+x)累加从1到x(bi)-累加从1~x(i*bi)
我们可以使用两个树状数组分别维护bi和i*bi的前缀和
*/
#include<bits/stdc++.h>
using namespace std;

typedef long long LL;

int n, m;
int const N = 1e5 + 10;
LL c1[N], c2[N];  // c1维护bi的前缀和，c2维护i*bi的前缀和
int a[N];
LL s[N];

int lowbit(int x) {
    return x & -x;
}

// 单点修改
void add(LL c[], int x, int y) {
    for (int i = x; i <= n; i += lowbit(i)) c[i] += (LL)y;
}

// 前缀和
LL query(LL c[], int x) {
    LL res = 0;
    for (int i = x; i; i -= lowbit(i)) res += c[i];
    return res;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);
        s[i] = s[i - 1] + 0ll + a[i];  // 计算原来的a[i]的前缀和
    }
    while (m--) {
        string op;
        int l, r, d;
        cin >> op;
        if (op[0] == ‘C‘) {
            cin >> l >> r >> d;
            add(c1, l, d), add(c1, r + 1, -d);  // 把[l, r]加d对c1来说就是把l和r+1分别增加d和减去d
            add(c2, l, l * d), add(c2, r + 1, -(r + 1) * d);  // 把[l, r]加d对c1来说就是把l和r+1分别增加l*d和减去(r+1)*d
        }
        else {
            cin >> l >> r;
            LL res = s[r] - s[l - 1];  // 原来的区间和
            res += ((1 + r) * query(c1, r) - query(c2, r) - (l * query(c1, l - 1) - query(c2, l - 1)));  // 加上改变值
            printf("%lld
", res );
        }
    }
    return 0;
}

3. 例题

acwing241楼兰图腾
有n个点，坐标分别为(1, y1), (2, y2), (3, y3), ..., (n, yn)
如果三个点(i, yi), (j, yj), (k, yk) 满足1 ≤ i < j < k ≤ n且yi > yj, yj < yk，则称这三个点构成V图腾;
如果三个点(i, yi), (j, yj), (k, yk)满足1 ≤ i < j < k ≤ n 且yi < yj, yj > yk，则称这三个点构成∧图腾;
求有多少个V图腾和∧图腾
n ~ 2e5, yi ~ 2e5

/*
使用树状数组去维护每个数字出现的次数的前缀和，c[i]记录i这个节点管辖的几个点的出现次数
统计时，只要统计每个点左边有多少个比他大，右边有多少个比他大，然后相乘就能够知道出现多少个^;
统计V则相反
*/
#include<bits/stdc++.h>
using namespace std;

typedef long long LL;

int n;
int const N = 2e5 + 10;
int a[N], c[N];
int gre[N], low[N];

int lowbit(int x) {
    return x & -x;
}

void add(int x, int y) {
    for (int i = x; i <= n; i += lowbit(i)) c[i] += y;
}

int query(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += c[i];
    return res;
}

int main() {
    cin >> n;
    for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
    LL res1 = 0, res2 = 0;
    for (int i = 0; i < n; ++i) {
        int y = a[i];
        gre[i] = query(n) - query(y);
        low[i] = query(y - 1);
        add(y , 1);
    }

    memset(c, 0, sizeof c);
    for (int i = n - 1; i >= 0; --i) {
        int y = a[i];
        res1 += (LL)gre[i] * (query(n) - query(y));
        res2 += (LL)low[i] * query(y - 1);
        add(y , 1);
    }
    cout << res1 << " " << res2 << endl;
    return 0;
}

acwing244谜一样的牛
有n头奶牛，已知它们的身高为 1~n 且各不相同，但不知道每头奶牛的具体身高。
现在这n头奶牛站成一列，已知第i头牛前面有Ai头牛比它低，求每头奶牛的身高。
1≤n≤10⁵

/*
本题可以从n往1向前看，如果他的前面有a[i]头牛比他低，那第i头牛的高度就是可以选择的身高的第i+1小。
因此可以给每个身高一个标值，1表示没被选，0表示被选中。那么寻找第a[i]+1个没被选中的牛就可以二分查找
前缀和等于a[i]+1的那个数字，树状数组维护这个前缀和即可
*/
#include<bits/stdc++.h>

using namespace std;

int n;
int const N = 1e5 + 10;
int c[N], a[N], ans[N];

int lowbit(int x) {
    return x & -x;
}

void add(int x, int y) {
    for (int i = x; i <= n; i += lowbit(i)) c[i] += y;
}

int query(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += c[i];
    return res;
}

int main()
{
    cin >> n;
    for (int i = 2; i <= n; ++i) scanf("%d", &a[i]);

    for (int i = 1; i <= n; ++i) c[i] = lowbit(i);  // 初始化，因为每个身高都没备选，那么都初始化为1，Tr数组就是区间的长度，即为lowbit(i)

    for (int i = n; i >= 1; --i)   // 倒着往前看
    {
        // 二分查找a[i]+1小
        int l = 1, r = n;  
        while (l < r)
        {
            int mid = (l + r) >> 1;
            if (query(mid) >= a[i] + 1) r = mid;
            else l = mid + 1;
        }
        ans[i] = l;  // 记录答案 
        add(l, -1);  // 这个牛被选了，从1变成0
    }
    for (int i = 1; i <= n; ++i) printf("%d
", ans[i]);
    return 0;
}

acwing260买票
给定n，表示游客的数目；随后n行，每行两个数，p[i]和v[i],分别表示当这个游客插队后，前面的人数以及这个游客的编号。求出当全部游客完成插队后，队列中的游客编号情况。
n ~ 2e5,P[i]、V[i] ~ short

// 本题的思路和acwing244一样，倒着往前看，插入前面人数+1的位置。
#include <bits/stdc++.h>

using namespace std;

int const N = 2e5 + 10;
int res[N], P[N], V[N], n, c[N];

typedef long long LL;

int lowbit(int x) {
    return x & -x;
}

void add(int x, int y) {
    for (int i = x; i <= n; i += lowbit(i)) c[i] += y;
}

int query(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += c[i];
    return res;
}

int main() {
    while (scanf("%d", &n) != EOF) {
        for (int i = 1; i <= n; ++i) {
            scanf("%d%d", &P[i], &V[i]);
            c[i] = lowbit(i);
        }
        for (int i = n; i >= 1; --i) {
            int pos = P[i] + 1;
            int l = 1, r = n;
            while (l < r) {
                int mid = l + r >> 1;
                if (query(mid) >= pos) r = mid;
                else l = mid + 1;
            }
            res[l] = V[i];
            add(l, -1);
        }
        
        for (int i = 1; i <= n; ++i) printf("%d ", res[i]);
        cout << endl;
    }
    return 0;
}