week4-D-Q老师染砖

Posted 2020-12-09 liuzhuan-xingyun

Description

衣食无忧的 Q老师 有一天突发奇想，想要去感受一下劳动人民的艰苦生活。

具体工作是这样的，有 N 块砖排成一排染色，每一块砖需要涂上红、蓝、绿、黄这 4 种颜色中的其中 1 种。且当这 N 块砖中红色和绿色的块数均为偶数时，染色效果最佳。

为了使工作效率更高，Q老师 想要知道一共有多少种方案可以使染色效果最佳，你能帮帮他吗？

Input

第一行为 T，代表数据组数。(1 ≤ T ≤ 100)

接下来 T 行每行包括一个数字 N，代表有 N 块砖。(1 ≤ N ≤ 1e9)

Output

输出满足条件的方案数，答案模 10007。

Sample Input

2
1
2

Sample Output

2
6

思路：

连续格子染色，很明显有子结构的性质，可以考虑 DP ，但是 n 很大，因此考虑矩阵快速幂优化 DP。
令 A[i] ，B[I] , C[i]表示 i 个格子，红绿均为偶数、均为奇数、有一个为偶数的染色方案数 。
则DP 转移方程 ：
A[i] = 2 * A[i-1] + C[i-1]
B[i] = 2 * B[i-1] + C[i-1]
C[i] = 2 * A[i-1] + 2 * B[i-1] + 2 * C[i-1]
不难看出，A[1]=2，B[1]=0，C[1]=2

矩阵快速幂

 

 

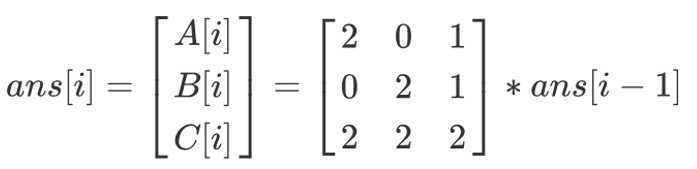
代码：

 1 #include<iostream>
 2 #include<cstring>
 3 using namespace std;
 4 const int  m=10007;
 5 /*
 6        2  0  1
 7 [i] =  0  2  1   [i-1]
 8        2  2  2
 9 
10 */
11 int n;
12 
13 struct Matrix {
14     int v[3][3];
15     Matrix() 
16     {
17         memset(v, 0, sizeof(v));
18     }
19     
20     Matrix operator *(Matrix const &b) const 
21     {
22         Matrix re;
23         for (int i = 0; i < 3; i++)
24         {
25             for (int j = 0; j < 3; j++)
26             {
27                 re.v[i][j] = 0;
28                 for (int k = 0; k < 3; k++)
29                 {
30                     re.v[i][j] += (v[i][k]*b.v[k][j])%m;    
31                 }
32                 re.v[i][j] %= m;
33             }
34                 
35         }            
36         return re;
37     }
38     
39 };
40 void init(Matrix& m){
41     m.v[0][0]=m.v[1][1]=m.v[2][2]=m.v[2][0]=m.v[2][1]=2;
42     m.v[0][1]=m.v[1][0]=0;
43     m.v[0][2]=m.v[1][2]=1;        
44 }
45 
46 Matrix quick_pow(Matrix a, int x) 
47 {
48     Matrix ret ;
49     ret.v[0][0]=2;
50     ret.v[1][0]=0;
51     ret.v[2][0]=2;
52     while (x) {
53         if (x & 1)
54             ret = a * ret;
55         a = a * a;
56         x >>= 1;
57     }
58     return ret;
59 } 
60 
61 int main()
62 {
63     int T;
64     cin>>T;
65     while(T--)
66     {
67         cin>>n;
68         Matrix a;
69         init(a);
70         a = quick_pow(a, n-1);
71         cout<<a.v[0][0]<<endl;
72     }
73  }