P3182 [HAOI2016]放棋子

Posted 2020-12-09 shikeyu

给你一个 N∗N的矩阵，每行有一个障碍，数据保证任意两个障碍不在同一行，任意两个障碍不在同一列，要求你在这个矩阵上放 N 枚棋子（障碍的位置不能放棋子），要求你放 N个棋子也满足每行只有一枚棋子，每列只有一枚棋子的限制，求有多少种方案。

错排问题指考虑一个有 n 个元素的排列，若一个排列中所有的元素都不在自己原来的位置上，那么这样的排列就称为原排列的一个错排。 n个元素的错排数记为 D(n) 。 研究一个排列错排个数的问题，叫做错排问题或称为更列问题。 ---《百度百科》

看上去这就是一个递推问题，那么递推式是如何推出来呢？ 当 n 个编号元素放在n个编号位置，元素编号与位置编号各不对应的方法数用 D(n) 表示，那么 D(n−1)就表示 n−1个编号元素放在 n−1个编号位置，各不对应的方法数，其它类推.
第一步，把第 nnn 个元素放在一个位置，比如位置 kkk ，一共有 n−1n-1n−1 种方法；
第二步，放编号为 k 的元素，这时有两种情况：⑴把它放到位置 n ，那么，对于剩下的 n−1个元素，由于第 k个元素放到了位置 n，剩下 n−2个元素就有 D(n−2) 种方法；⑵第 k个元素不把它放到位置 n，这时，对于这 n−1n-1n−1 个元素，有 D(n−1)D(n-1)D(n−1) 种方法；
综上得到
D(n)=(n−1)∗(D(n−2)+D(n−1))
特殊地，D(1)=0,D(2)=1

知道了这个之后，这题就是一个裸的高精了。

 

 

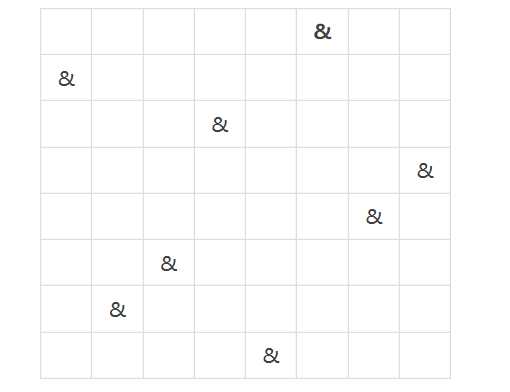
&表示障碍物，那么可以抽象的理解为一个排列：7,2,3,6,1,8,4,5（看表格中每列障碍物的“高度”）

同理，对于所有满足同一列只有一个棋子且同一行只有一个棋子的摆放方式，也可以化为一个排列。

但是题目还有一个条件，棋子不能放在障碍物上。所以这就是个错排问题

#include<cstdio>
using namespace std;
// D(n)=(n-1)*(D(n-1)+D(n-2))
// D(1)=0 D(2)=1

int n;
int D[205][100005];

void ad(int now){
    int x=0;
    for(int i=1;i<100005;i++){
        D[now][i]=D[now-1][i]+D[now-2][i]+x;
        x=D[now][i]/10;
        D[now][i]%=10;
    }
    x=0;
    for(int i=1;i<100005;i++){
        D[now][i]=D[now][i]*(now-1)+x;
        x=D[now][i]/10;
        D[now][i]%=10;
    }
}

signed main(){
    scanf("%d",&n);
    D[2][1]=1;
    if(n==1||n==2){
        printf("%d",n-1);
        return 0;
    }
    for(int i=3;i<=n;i++)
        ad(i);
    int lenc=100004;
    while(D[n][lenc]==0) lenc--;
    while(lenc) printf("%d",D[n][lenc--]);
    return 0;
}