数组稀疏矩阵广义表综合应用

Posted 2020-12-08 wangzheming35

本章节题目在以前学习的算法很美中同步了很多一样的思想，值得去好好思考。

题一

已知R[0，...，n-1]（n>1）为整型数组，设计实现下列算法的递归算法

（1）求数组R中最大整数

（2）求n个整数之和

（3）求n个整数平均值（结果用float表示）

//强调递归
int getMax(int R[],int n)
{
    int m;
    if(n==1)
        return R[0];
    else
    {
        m=getMax(R,n-1);   //此处运用分治法的思想
        if(R[n-1]>m)
            return R[n-1];
        else
        {
            return m;
        }
    }
}

int getSum(int R[],int n)
{
    if(n==1)
        return R[0];
    else
    {
        return (R[n-1]+getSum(R,n-1));
    }
}

float getAvg(int R[],int n)
{
    if(n==1)
        return R[0];
    else
    {
        return (R[n-1]+(n-1)*getAvg(R,n-1))/n;
    }
}

题二

一个n阶矩阵A[0，...n-1，0...，n-1]采用一维数组S[0,1，...，n(n+1)/2-1]按行序为主序存放其上三角各元素，编写一个算法求A[i] [j]在S[k]中位置

//因为是n×n阶矩阵，故i=j,存放至上三角
void find_position(int i,int j,int &k,int n)
{
    k=(i*(2n-i+1)/2+j-i);
    // If下三角：k=(i(i+1)/2+j);
}

题三

设计一个算法，将A[0...n-1]中所有奇数移到偶数之前。要求除数组A[]之外的空间消耗O(1)，且时间复杂度O(n)

//双指针双向扫描，i指向左边偶数，j指向右边奇数
void move(int A[],int n)
{
    int i=0,j=n-1,temp;
    while(i<j)
    {
        while(A[i]%2==1&&i<j)   //A[i]为一个偶数
            ++i;
        while(A[j]%2==0&&i<j)   //A[j]为一个奇数
            --j;
        if(i<j)
        {
            temp=A[i];
            A[i]=A[j];
            A[j]=temp;
            ++i;
            --j;
        }
    }
}

题四

一个m×n矩阵存储在二维数组A[maxSize] [maxSize]中

（1）求数组A靠边元素之和（最外围4条边上的元素和）

（2）求从A[0] [0]开始的互不相邻的各元素之和

（3）m=n时，分别求两条对角线上的元素之和，否则打印m≠n的信息

int get_outEdges(int A[][maxSize],int m,int n)
{
    int s=0,i,j;
    for(i=0;i<m;++i)   //第一列
        s=s+A[i][0];
    for(i=0;i<m;++i)   //最后一列
        s=s+A[i][n-1];
    for(j=0;j<n;++j)   //第一行
        s=s+A[0][j];
    for(j=0;j<n;++j)   //最后一行
        s=s+A[m-1][j];
    //要减去4个角重复元素
    return (s-A[0][0]-A[0][n-1]-A[m-1][0]-A[m-1][n-1]);
}

int nonAdjacent_sum(int A[][maxSize],int m,int n)
{
    int s=0,i,j;
    do{
        j=0;
        do
    	{
        	s=s+A[i][j];
        	j=j+2;   //跳过一列
    	}while(j<n);
    	i=i+2;   //跳过一行
    }while(i<m);
    return s;
}

int diagonal_sum(int A[][msxSize],int m,int n)
{
    int s=0,i;
    if(m!=n)
        printf("m≠n");
    return -1;
    else
    {
        for(i=0;i<m;++i)
            s=s+A[i][i];   //主   
        for(i=0;i<n;++i)
            s=s+A[n-i-1][i];   //副
    }
    return s;
}

题五

已知A和B为两个n×n阶的对称矩阵，输入时，对称矩阵只输入下三角形元素，按行存入一维数组，设计一个算法求对称矩阵A和B的乘积

int getVelue(int a[],int i,int j)
{
    if(i>=j)
        return a[(i*(i-1))/2+j];
    else
        return a[(j*(j-1))/2+i];
}

void mult(int a[],int b[],int c[][maxSize],int n)
{
    int sum=0;
    for(int i=0;i<n;++i)
        for(j=0;j<n;++j)
        {
            for(int k=0;k<n;++k)
                sum+=getValue(a,i,k)*getValue(b,k,j);
            c[i][j]=sum;
        }
}

题六

说明稀疏矩阵的三元组存储结构并实现稀疏矩阵的创建和查找操作

三元组的存储结构是一种顺序结构，顺序表中的每个结点对应稀疏矩阵的一个非0元素，三个字段分别是行下标、列下标和值。这里用第0行第一个元素存储矩阵行数，第0行第二个元素存储矩阵列数，第0行第三个元素存储矩阵非0个数

void create(int (*A)[4],int m,int n,int B[][3])
{
    int i,j,k=1;
    for(i=0;i<m;++i)
        for(j=0;j<n;++j)
            if(A[i][j]!=0)
            {
                B[k][0]=i;
                B[k][1]=j;
                B[k][2]=A[i][j];
                ++k;
            }
    B[0][0]=m;
    B[0][1]=n;
    B[0][2]=k-1;
}

int find(int A[][3],int x)
{
    int i=1,t;
    t=A[0][2];
    while(i<=t&&A[i][2]!=x)
        ++i;
    if(i<=t)
        return 1;
    else
        return 0;
}

题七

//我们可以取到 下标（a2，n-2，n-1，n） ，...，（an-1，1,2,3）
//前i-1行共有非0元素3*(i-1)个
//在非0的ai，j前，本行还有非0元素个数j-(n-i)个
int getValue(int a[],int i,int j)
{
    int add;
    if(i>1&&i<n&&j>=n-i&&j<=n-i+2)
    {	
        add=1+3*(i-2)+(i+j-n);   //B中下标
        return a[add];
    }
}

题八

void matrix_add(int A[],int B[],int C[])
{	
    //i为A的下标，j为B的下标，k为C的下标，皆从0开始
    int i=0,j=0,k=0,m;
    while(A[i]!=-1&&B[j]!=-1)   //循环直到A或B结束
    {
        if(A[i]==B[j])   //行相等
        {
            if(A[i+1]==B[j+1])   //列相等
            {
                m=A[i+2]+B[j+2];
                if(m!=0)
                {
                    C[k]=A[i];
                    C[k+1]=A[i+1];
                    C[k+2]=m;
                    k=k+3;
                }
                i=i+3;
                j=j+3;
            }
            else if(A[i+1]<B[j+1])
            {
                //A的列小于B的列，将A的3个元素直接放入C
                {
                    C[k]=A[i];
                    C[k+1]=A[i+1];
                    C[k+2]=A[i+2];
                    k=k+3;
                    i=i+3;
                }
                else
                {
                    //B的列小于A的列，将B的3个元素直接放入C
                    C[k]=B[j];
                    C[k+1]=B[j+1];
                    C[k+2]=B[j+2];
                    k=k+3;
                    j=j+3;
                }
            }
            else if(A[i]<B[i])
            {
                //A的行小于B的行，将A的3个元素直接放入C
                C[k]=A[i];
                C[k+1]=A[i+1];
                C[k+2]=A[i+2];
                k=k+3;
                i=i+3;
            }
            else
            {
                //B的行小于A的行，将B的3个元素直接放入C
                C[k]=B[j];
                C[k+1]=B[j+1];
                C[k+2]=B[j+2];
                k=k+3;
                j=j+3;
            }
        }
        //循环结束
        if(A[i]==-1)
            while(B[j]!=-1)
            {
                C[k]=B[j];
                C[k+1]=B[j+1];
                C[k+2]=B[j+2];
                k=k+3;
                j=j+3;
            }
        else
            while(A[i]!=-1)
                C[k]=A[i];
                C[k+1]=A[i+1];
                C[k+2]=A[i+2];
                k=k+3;
                i=i+3;
    }
    C[k]=-1;
}

题九

写出广义表的结点结构设计，在此基础上编写遍历广义表的递归算法，按照广义表的逻辑结构顺序，打印广义表所有原子结点上的数据域，如，广义表(a,(b,c,d),e,(f,g))输出结果：a,b,c,d,e,f,g

结构体设计：

typedef struct gNode()
{
    int tag;   //0代表原子结点，1代表表结点
    struct gNode *link;
    union
    {
    	char data;
        struct gNode *sList;
    }val;
}gNode;

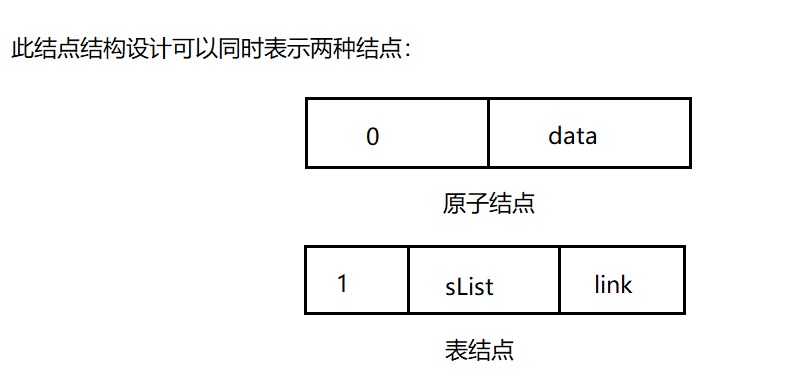
运用union关键字，使val变量中的两个分量data和slist共享同一片存储空间，这里是因为广义表结点不可能既是原子结点又是表结点，如果data和slist各用一个空间太浪费

遍历算法：

void travel(gNode *p)
{
    if(p!=NULL)
    {
        if(p->tag==0)
            printf("%c",p->val.data);
        else
            travle(p->val.sList);
        if(p->link!=NULL)
            travle(p->link);
    }
}

题十

设计一个计算广义表长度（指其第一层元素个数）的算法，如：(a,(b,c,d),((e),f)) 长度为3

int getLength(gNode *p)
{
    int n=0;
    if(p!=NULL&&p->tag==1)
    {
        while(p!=NULL)
        {
            p=p->link;
            ++n;
        }
        return n;
    }
    else
        return 0;
}