机器学习算法原理与实践-朴素贝叶斯（文章迁移）

Posted 2020-12-08 gdut1425

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习算法原理与实践-朴素贝叶斯（文章迁移）相关的知识，希望对你有一定的参考价值。

文章迁移说明：此文已由lightinglei于2019-02-18发布，是本人的另外一个账号，现同步迁移至本账号

一、朴素贝叶斯原理介绍

书籍上对概念的介绍，因引入了很多数学符号，看起来比较晦涩难懂，下面我们以案例的形式先带大家回顾下概率的一些基本知识点，下表为互联网行业不同岗位、不同体重是否会被女神喜欢（纯属虚构，哈哈~）

技术图片

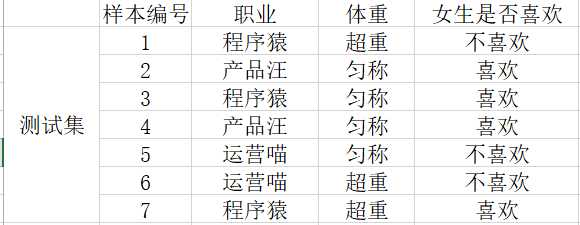
先通过几个小问题回顾下知识点：

1）女生喜欢的概率：用P代表概率，“喜欢”占4个，“不喜欢”占3个，则P（喜欢）=4/7

2）职业是产品汪并且体型匀称的概率：样本总共7个，匀称的产品汪有2个，则P（产品汪，匀称）=2/7

3) 女生喜欢的条件下，职业是程序猿的概率：样本中满足女生“喜欢”的样本有4个，其中是程序猿的概率有2个，则：P（程序猿|喜欢）=1/2

4）女生喜欢的条件下，职业是程序猿，体重超重的概率：样本中满足女生“喜欢”的样本有4个，超重的程序猿只有1个，则：P（程序猿，超重|喜欢）=1/4

这时候再来认识联合概率、条件概率就好理解了，将P（产品汪，匀称）称之为联合概率，P（程序猿|喜欢）称之为条件概率，其具体定义如下：

联合概率：包含多个条件，且所有条件同时成立的概率，记为：P(A,B)

条件概率：事件A在另外一个时间B已经发生的条件下发生的概率，记为:P(A|B)，如P（产品汪，超重|喜欢）也属于条件概率

还有一个知识点，在朴素贝叶斯中非常重要，就是特征的相互独立

相互独立：如果P(A,B)=P(A)*P(B)，则称事件A和事件B相互独立，这是个充分必要条件，“朴素”一词就是在假定各个特征相互独立的条件下

接下来，再来解决这样一个问题，已知小王是产品汪，体重超重，是否会被女神喜欢？

通过前面的知识点，化成求解的目标为：P（喜欢|产品汪，超重)，求解这个目标，就需要引入贝叶斯公式了，先来看下公式的具体定义：

贝叶斯公式：

技术图片

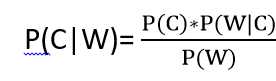
其中，W为特征值（如职业、体重），C为类别（如女生是否喜欢），则：

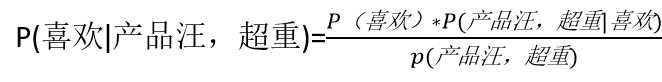技术图片，P（喜欢）=4/7，则还需要求出P（产品汪，超重）和P(产品汪，超重|喜欢）

因表格训练集样本数量有限，不能直接求出P（产品汪，超重），朴素贝叶斯可解决这个问题，前面提到，“朴素”是特征相互独立的意思，而相互独立的特征的公式P(A,B)=P(A)*P(B)

因此，可将P（产品汪，超重）=P（产品汪）*P（超重）=2/7*3/7=6/49，

同理：P(产品汪，超重|喜欢）=P(产品汪|喜欢）*P（超重|喜欢）=1/2*1/4=1/8，假设前提：产品汪这个专业与体重超重无关

则P(喜欢|产品汪，超重）=7/12，从结论来看，超重的产品汪有超过一半的概率会被女生喜欢，与现实应该会存在差异（haha~~），出现的这样情况主要是因为两个原因，一个是训练样本量太少，还有一个是刚才的假设前提，事实上可能产品汪与体重超重并不独立，而我们强制假设独立成立，所以有时候会牺牲掉一定的分类准确率，这也是朴素贝叶斯的特点。

注意：如果需要求P(运营喵|喜欢)的概率呢，由于样本少，则按照上表计算是0，与事实会有差异，为了解决这个问题，需要引入拉普拉斯平滑系数，以下为其详细定义:

拉普拉斯平滑系数:

,a为指定的系数一般为1，m为训练集中不同职业的个数

则P(运营喵|喜欢)通过拉普拉斯系数变化后：

二、朴素贝叶斯实践

本节采用scikit-learn库，其API为sklearn.naive_bayes.MultinomialNB(alpha=1.0)，朴素贝叶斯分类，alpha为拉普拉斯平滑系数

以下案例为sklearn中的数据集，20newsgroups数据集是用于文本分类、文本挖据和信息检索研究的国际标准数据集之一。数据集收集了大约20,000左右的新闻组文档，均匀分为20个不同主题的新闻组集合

其算法实现流程为：获取数据集->特征工程->训练模型->模型评估

"""
date:2019.1.25
author：lightinglei
朴素贝叶斯学习总结：
1.贝叶斯公式：P(Y|X)=P(X|Y)P(Y)/P(X)
P(X|Y)=P(x1|Y)P(x2|Y)?P(xn|Y)
X：为特征向量，Y:类别
先验概率P（X)：是指根据以往经验和分析得到的概率
后验概率P(Y|X)：事情已经发生，要求这件事情发生的原因是由某个因素引起的可能性大小
条件概率P(X|Y)：在已知类别的情况下，出现特征值X的概率密度
朴素：特征相互独立，贝叶斯值的是贝叶斯公式，其朴素贝叶斯公式可以如下所示：
那么贝叶斯公式中P(X|Y)可写成 P(X|Y)=P(x1|Y)P(x2|Y)?P(xn|Y)
其中P（A,B)=P(A)*P(B)是A和B相互独立的充分必要条件
所以朴素贝叶斯公式也可生成：
P(Y|X)=P(x1|Y)P(x2|Y)?P(xn|Y)P(Y)/P(X)
2.优缺点分析：
1）优点：朴素贝叶斯来源于古典的数学理论，有稳定的分类效率；对缺失数据不太敏感，算法也比较简单，常用语文本分类；
分类准确度高，速度快
缺点：因假定特征之间是相互独立，若实际存在关联，则效果不好
"""
from sklearn.naive_bayes import GaussianNB 
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB #朴素贝叶斯
from sklearn.model_selection import GridSearchCV
def nb_news():
    # 1.获取数据
    news=fetch_20newsgroups(subset="all")
    # 2.划分数据集
    x_train,x_test,y_train,y_test=train_test_split(news.data,news.target)
    # 3.特征工程:文本特征抽取tf-idf
    transfer=TfidfVectorizer() #统计特征词出现的个数
    x_train=transfer.fit_transform(x_train)
    x_test=transfer.transform(x_test)
    # 4.训练朴素贝叶斯模型
    estimator=MultinomialNB() # 实例化对象
    estimator.fit(x_train,y_train)#训练模型
    predict_y = estimator.predict(x_test)
    # 5. 模型评估
    print("测试集的预测值为：
", predict_y)
    print("真实值与预测值的对比为：
", y_test == predict_y)
    accuracy = estimator.score(x_test, y_test)  # 测试集在训练集上的准确率
    print("准确率为：
", accuracy)

    return None

if __name__=="__main__":
    nb_news()
542020373514432


"""
其运行结果为：
测试集的预测值为：
 [10 17  9 ... 15 14  1]
真实值与预测值的对比为：
 [ True  True  True ...  True  True  True]
准确率为：
 0.8542020373514432
"""