max_heap与min_heap

Posted 2020-12-07 yuanwebpage

1. 基本概念

max_heap，min_heap是一颗堆树。其定义如下：

(1) 堆树是一颗完全二叉树;

(2) 根节点的值大于子节点(max_heap)；对于·min_heap，根节点的值小于子节点；

(3) 左右子树也是一颗堆树。

比如下面的完全二叉树，就是一个max_heap:

                                                     

 

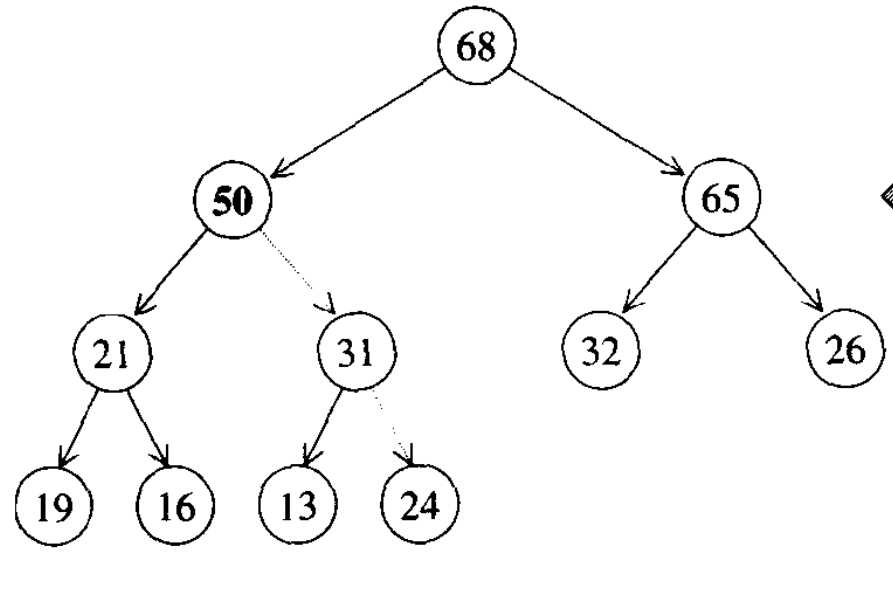
　　回想完全二叉树的性质(一个节点编号为i，如果其左右子树和父节点存在，那么左子树编号2i,右子树编号2i+1,父节点编号i/2)，可以用数组来存储完全二叉树。令数组a[0]为空，从a[1]开始存储，那么就是一个完全二叉树。因此，max_heap或min_heap的底层存储结构就是一个数组(数组从编号1开始存储)，下面的讲解都将以max_heap为例。对于一个max_heap，主要的操作有四个：make_heap(构造一个max_heap)，

push_heap(向二叉树添加节点)，pop_heap(取最大值，即根节点)，sort_heap(对一个max_heap排序)。

2. 基本操作

2.1 push_heap

　　将一个数放入max_heap采用一种上溯(percolate up)的方法。首先将数存到max_heap数组末尾，然后与其父节点比较，如果大于父节点则与其交换，此时完成一层上溯；然后继续与父节点比较，继续上溯，直到小于父节点的值。以下图的max_heap为例：

                                      

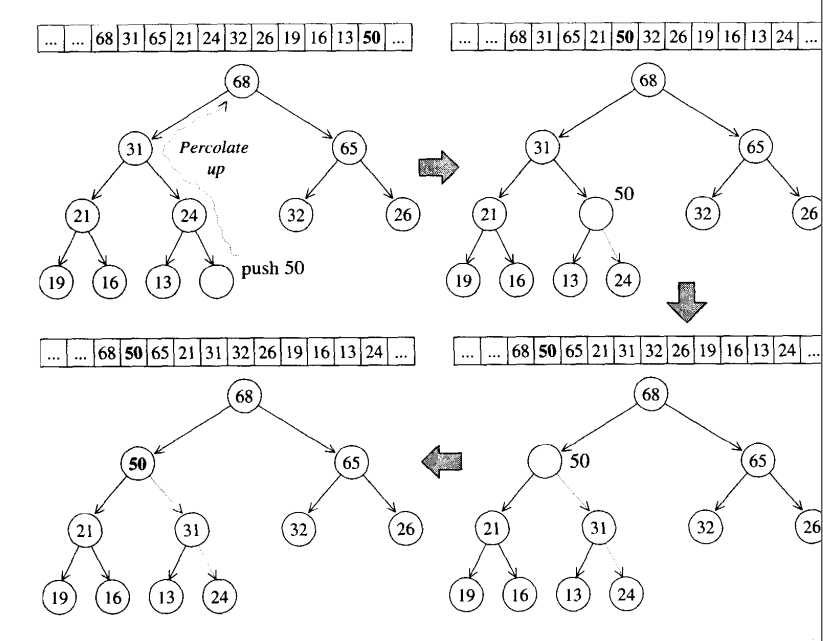
设存储max_heap数组的名字为max_heap

(a) 在原max_heap[11]中插入50;

(b) max_heap[11]与max_heap[11/2]比较，大于父节点，交换；

(c) max_heap[11/2]即max_heap[5]继续与max_heap[5/2]比较，大于父节点，交换；

(d) max_heap[2]与max_heap[2/2]比较，小于父节点，停止，push_heap成功 。

2.2 pop_heap

　　将最大元素即max_heap首元素删除，采用下溯(percolate down)的方法。首先将数组首元素与尾元素交换，相当于尾元素变成了根节点。然后根节点与其左右子节点比较，将其与大于它的最大子节点交换位置，下溯一层；然后重复以上操作。以下图的max_heap为例：

                                                

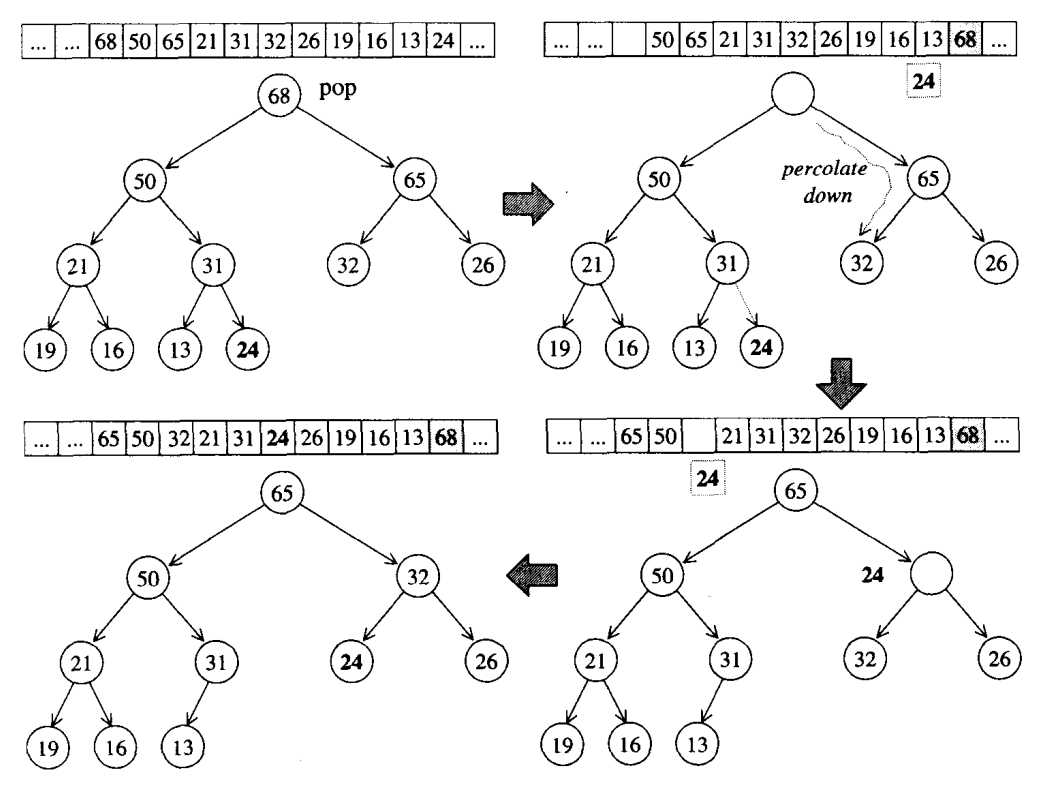
设存储max_heap数组的名字为max_heap

(a) 将根节点max_heap[1]与max_heap[max_heap.size()-1]交换，即68和24交换；

(b) 此时24在根节点，与其子节点比较，与较大的子节点交换位置，即24(max_heap[1])和65(max_heap[1*2+1])交换；

(c) 24接着与其子节点比较并与大于它的最大子节点交换，即24与32交换；

(d) 此时24没有子节点，交换完成。

注：通过pop_heap之后，最大根节点到了数组末尾，此时删除或取值都行。

2.3 sort_heap

由于pop_heap可以将最大节点放置到数组末尾，所以对一个max_heap一直执行pop_heap操作，就能得到一个递增的排序后的数组。

2.4 make_heap

make_heap给定一个数组，构造max_heap,主要步骤如下：

假设给定数组元素个数为n

(1) 构造完全二叉树，即从max_heap[1]开始存储数组元素；

(2) 从第一个有子节点的数组出发(序号为n/2)，将其构在为max_heap(将其与最大子节点交换位置);

(3) 从n/2开始往前遍历(for i=n/2;i>0;i++)，对每个节点，都进行max_heap的构造(即对当前节点采用percolate down的方法)。

以数组a=[ 20，12，35，15，10，80，30，17，2，1 ]为例，其完全二叉树构造如下图：

                                                   

 

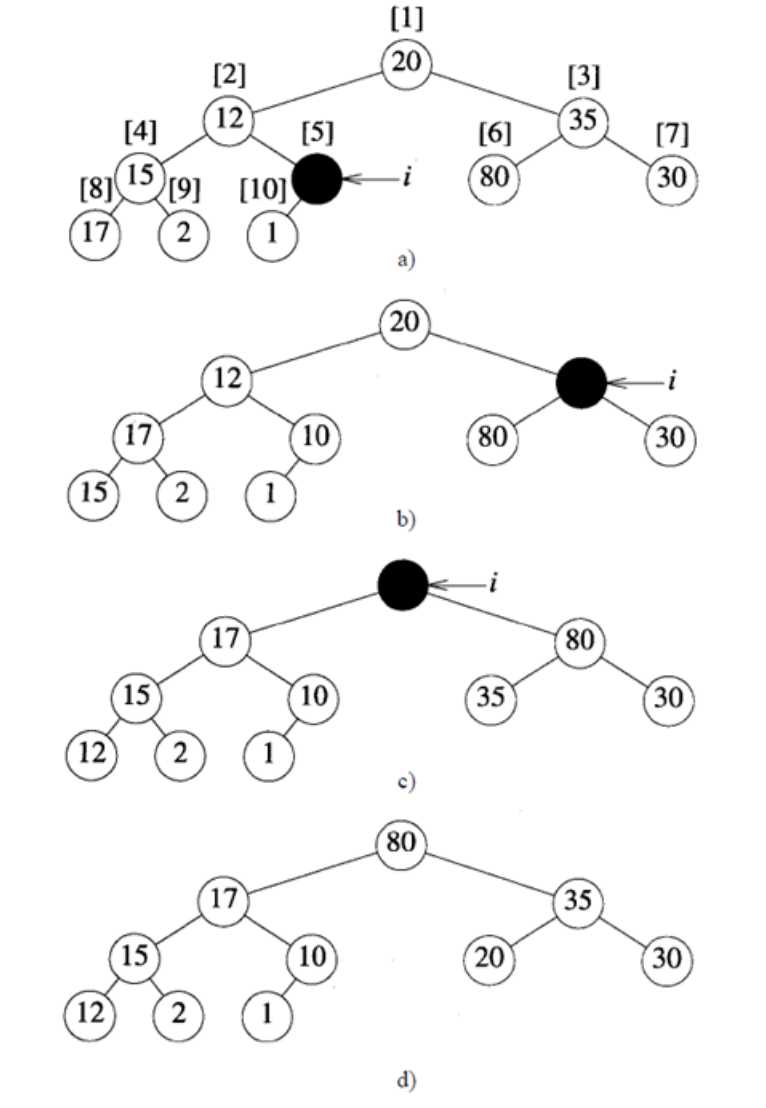
(a) 从5开始，由于a[5]>a[10]已经是max_heap; 再看a[4]，由于a[4]<a[8],交换a[4],a[8],此时以a[4]为根节点的子树已经是max_heap。经过以上两步，新的树如图b)。

(b) 再看a[3],由于a[3]<a[6]，交换a[3],a[6]; 再看a[2]，由于a[2]<a[4]，交换a[2]，a[4]。经过以上两步，新的树如图c)。

(c) 再看a[1]，由于a[1]<a[3]，交换a[1],a[3]，此时遍历完成，最终的max_heap如图d)所示。

3. 算法实现

 根据2中的算法思想，编写代码实现以上四个函数。C++实现如下：

  1 template<class T>
  2 
  3 //首先调用makeHeap，将数据成员heap变成最大堆，才能接着使用popHeap,pushHeap
  4 //sortHeap将输入的最大堆变成递增输出
  5 class MaxHeap
  6 {
  7 public:
  8     MaxHeap();
  9     vector<T>& getMaxHeap()
 10     {
 11         return heap;
 12     }
 13     void printHeap()   //访问heap数据成员
 14     {
 15         if (heap.size() < 1) return;
 16         for (int i = 1; i < heap.size(); i++)
 17             cout << heap[i] << "  ";
 18         cout << endl;
 19     }
 20 
 21     void pushHeap(T value);
 22     T popHeap();  //返回最大元素，并删除最大元素
 23     void sortHeap(vector<T>& oldHeap);
 24     void makeHeap(vector<T> vec);
 25 private:
 26     vector<T> heap;
 27     int maxIdx; //最后一个元素的下标
 28 };
 29 
 30 template<class T>
 31 MaxHeap<T>::MaxHeap()
 32 {
 33 }
 34 
 35 template<class T>
 36 void MaxHeap<T>::makeHeap(vector<T> vec)
 37 {
 38     int n = vec.size();
 39     heap.resize(n + 1);
 40     maxIdx = n;
 41     for (int i = 1; i < n + 1; i++)
 42         heap[i] = vec[i - 1];
 43     for (int i = maxIdx / 2; i > 0; i--)
 44     {
 45         int parentIdx = i; //父节点下标
 46         int childIdx = 2 * i; //孩子节点的下标
 47         while (childIdx <= maxIdx) {
 48             if (childIdx + 1 <= maxIdx && heap[childIdx + 1] >= heap[childIdx] && heap[childIdx + 1] > heap[parentIdx]) //右孩子最大
 49             {
 50                 swap(heap[parentIdx], heap[childIdx + 1]);
 51                 parentIdx = childIdx + 1;
 52             }
 53             else if (heap[childIdx] > heap[parentIdx]) //左孩子最大
 54             {
 55                 swap(heap[parentIdx], heap[childIdx]);
 56                 parentIdx = childIdx;
 57             }
 58             else
 59                 break;
 60             childIdx = 2 * parentIdx;
 61         }
 62     }
 63 }
 64 
 65 template<class T>
 66 void MaxHeap<T>::pushHeap(T value)
 67 {
 68     heap.push_back(value); //先构造完全二叉树
 69     maxIdx++;
 70     int i = maxIdx;
 71     while (i!=1 && heap[i] > heap[i / 2]) {
 72         swap(heap[i], heap[i / 2]);
 73         i = i / 2;
 74     }
 75 }
 76 
 77 template<class T>
 78 T MaxHeap<T>::popHeap()
 79 {
 80     if (maxIdx == 0) {
 81         cout << "empty MaxHeap" << endl;
 82     }
 83     swap(heap[1], heap[maxIdx]);
 84     int i = 1;
 85     int ci = 2 * i; //左孩子节点
 86     while (ci<maxIdx) {
 87         if (ci + 1 < maxIdx && heap[ci] < heap[ci + 1] && heap[i] < heap[ci + 1]) //右孩子最大
 88         {
 89             swap(heap[i], heap[ci + 1]);
 90             i = ci + 1;
 91         }
 92         else if (heap[ci] > heap[i]) //左孩子最大
 93         {
 94             swap(heap[i], heap[ci]);
 95             i = ci;
 96         }
 97         else
 98             break;
 99         ci = 2 * i;
100     }
101     T tmp = heap.back();
102     heap.pop_back();
103     maxIdx--;
104     return tmp;
105 }
106 
107 template<class T>
108 void MaxHeap<T>::sortHeap(vector<T>& oldheap) //传入参数必须是maxHeap
109 {
110     oldheap.insert(oldheap.begin(), oldheap[0]); //0为填充
111     int n = size(oldheap)-1;
112     int endIdx = n;
113     for (int k = 1; k < n; k++)
114     {
115         //此段代码与pop_heap基本一致
116         swap(oldheap[1], oldheap[endIdx]);
117         int i = 1;
118         int ci = 2 * i; //左孩子节点
119         while (ci < endIdx) {
120             if (ci + 1 < endIdx && oldheap[ci] < oldheap[ci + 1] && oldheap[i] < oldheap[ci + 1]) //右孩子最大
121             {
122                 swap(oldheap[i], oldheap[ci + 1]);
123                 i = ci + 1;
124             }
125             else if (oldheap[ci] > oldheap[i]) //左孩子最大
126             {
127                 swap(oldheap[i], oldheap[ci]);
128                 i = ci;
129             }
130             else
131                 break;
132             ci = 2 * i;
133         }
134         endIdx--; //每次排序后，最后一个元素就是最大，所以无序数组的下标要减少
135     }
136     oldheap.erase(oldheap.begin()); //去掉填充位
137 }

为了验证以上代码合理性，利用STL自带的make_heap，sort_heap，pop_heap，push_heap进行对照：

 1 int main()
 2 {
 3     vector<int> heap1 = { 0,1,2,3,4,8,9,3,5 };
 4     make_heap(heap1.begin(), heap1.end()); //STL自带的
 5     for (int i = 0; i < size(heap1); i++)
 6         cout << heap1[i] << "  ";
 7     cout << endl;
 8 
 9     vector<int> vec = { 0,1,2,3,4,8,9,3,5 };
10     MaxHeap<int> heap2;
11     heap2.makeHeap(vec);
12     heap2.printHeap();
13 
14     
15     heap1.push_back(7);
16     push_heap(heap1.begin(), heap1.end());
17     for (int i = 0; i < size(heap1); i++)
18         cout << heap1[i] << "  ";
19     cout << endl;
20 
21     heap2.pushHeap(7);
22     heap2.printHeap();
23 
24 
25     pop_heap(heap1.begin(), heap1.end());
26     cout << heap1.back()<<endl; //自带的库函数不会删除最大的元素
27     heap1.pop_back();
28     for (int i = 0; i < size(heap1); i++)
29         cout << heap1[i] << "  ";
30     cout << endl;
31 
32     cout << heap2.popHeap() << endl;
33     heap2.printHeap();
34 
35 
36     vector<int> tmpheap = heap1;
37     sort_heap(heap1.begin(), heap1.end());
38     for (int i = 0; i < size(heap1); i++)
39         cout << heap1[i] << "  ";
40     cout << endl;
41 
42     heap2.sortHeap(tmpheap);
43     for (int i = 0; i < size(tmpheap); i++)
44         cout << tmpheap[i] << "  ";
45     cout << endl;
46     
47 
48     system("pause");
49 }

PS: STL的最大堆函数需要包含头文件#include <algorithm>