《非线性科学中的现代数学方法：综述》

Posted 2020-12-07 cx2016

非线性科学中的现代数学方法：综述

Ch0【引言】

本文是作者作为数理经济学博士毕业后，对于自己在数学领域多年所学的一个总结，力图在极度繁杂的数理知识体系中摘选出那些最广泛应用的核心工具及思想。
本文主要关注的问题都是非线性的、动态的。具体地讲，主要涉及的是：微分动力系统、泛函的最优化初步（但不涉及最优控制及微分博弈，这块内容会另立文章。）

Ch1【动态系统理论】

——1.1 局部理论
线性系统的动态行为是人类研究得比较透彻的领域，而非线性动力学的研究则是相当困难的。实践中，我们面对一个非线性动力学系统，总是首先想到在工作点附近将其线性化，将其作为一个局部线性的系统加以研究（Hartman-Grobman 定理）。可线性化的非线性动力学系统局部拓扑等价于其线性化系统（下图清楚地展示了非线性系统与线性系统的拓扑等价）。在这里，研究可线性化系统局部稳定性问题时，非线性映射的 Jacobi 矩阵及其谱半径（请与线性泛函理论联系起来）的估计起到了核心作用。

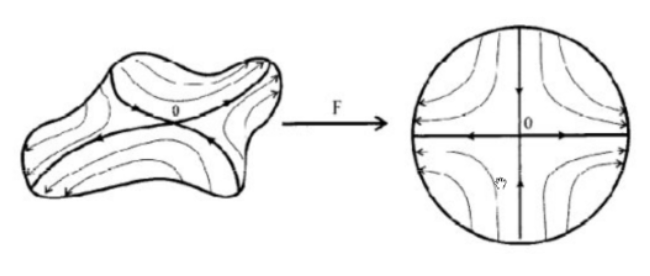
对于 Jaboci 矩阵特征值为 0 的特殊情况，我们就不能使用强大的 Hartman 线性化定理，这时候需要所谓的 "中心流形定理"。该定理的思想是将原本的复杂高维非线性系统降维到它的中心流形上，研究它在中心流形上的拓扑性质（比如稳定性、分岔等），从而得出原系统的局部动态行为。

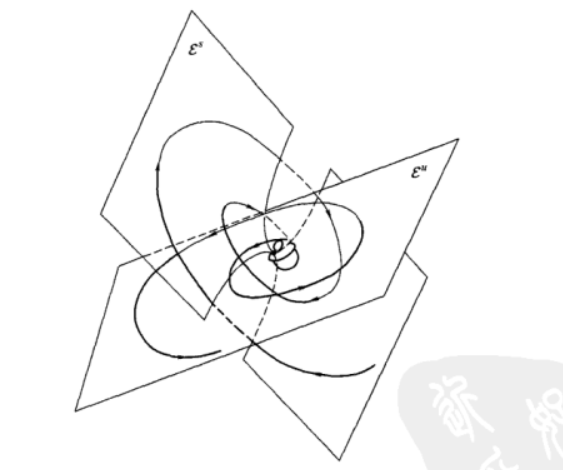
上图展示的一个线性系统具备有稳定子空间 

 和不稳定子空间 

 。对于非线性系统，相应的稳定流形

 与不稳定流形 

 ，与线性化系统的稳定子空间与不稳定子空间相切。如下图所示。

 

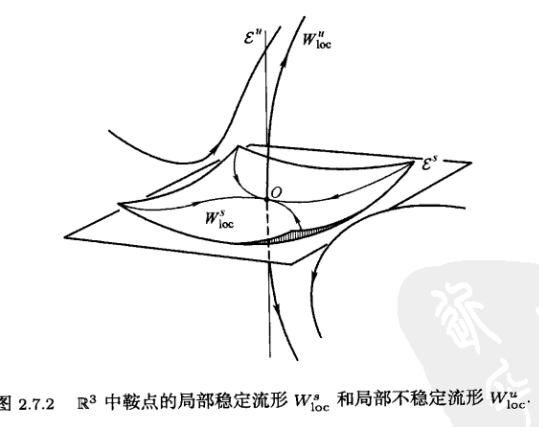
——1.2 全局理论
研究紧流形上动态系统的全局性质，我们常用的方法就是李雅普诺夫（Liapunov）函数法。但要注意，紧流形的紧性是不可或缺的。

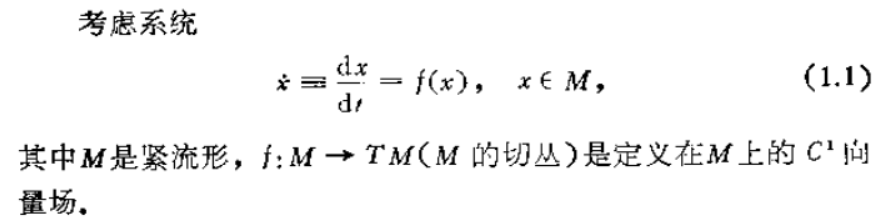
下面这段的内容可能是艰深的。
除此之外，微分拓扑中的 Poincare-Hopf 定理将流形上动态系统孤立零点（孤立平衡点）的拓扑度（Brouwer 度）与同调群的维数联系起来，非常深刻。工程类以及数理经济类的学者可能对同调论非常陌生，但并不影响本文的阅读体验。我们可以用这个定理来估计高维流形上非线性动态系统的平衡点的个数。可以设想，如果系统有非常多的孤立零点，那么它的相轨迹可能是极端复杂的。一般地，我们都是研究紧流形上的动态系统，想办法构造在边界上指向流形内部的向量场，依据 Hopf 定理，我们可以导出孤立零点 Brouwer 指数和为 1 的结论，为高维流形上非线性动力学相轨迹的全局性态奠定了 "拓扑" 的基调。

这些内容光说肯定不行，看图。

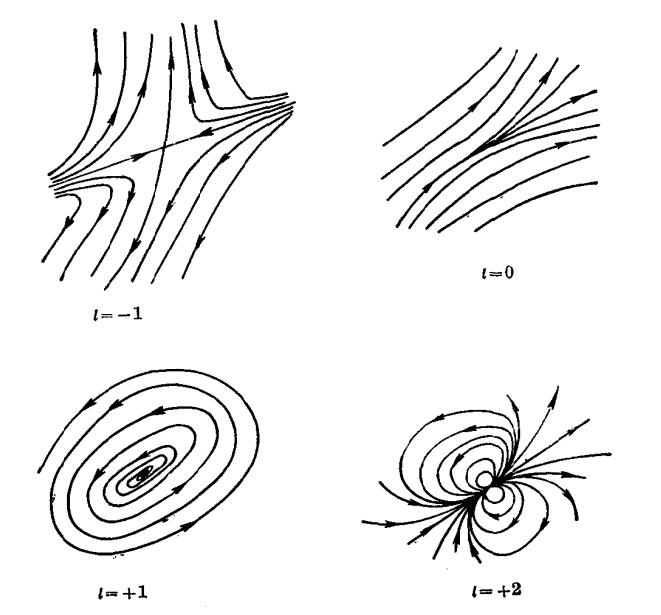
比如，如果孤立零点的指数是 - 1，那么该平衡点就是动力系统的鞍点。

接下来考察一个 3 维欧几里德空间中的 2 维流形（一个半球面），你一定会深有感触：

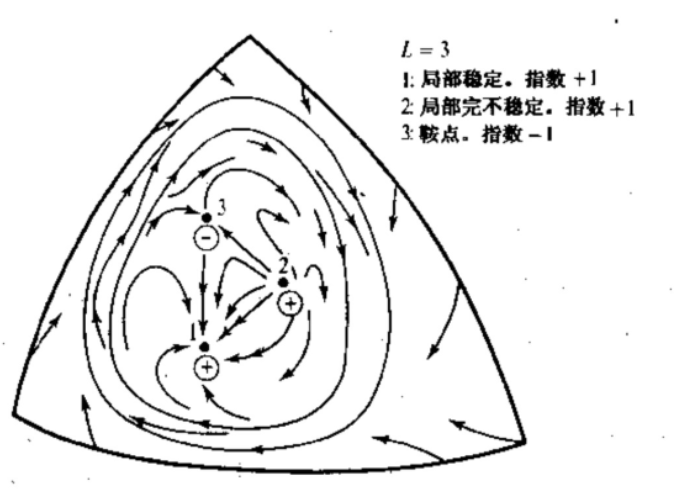
由于向量场边界指向内部，由 Poincare-Hopf 定理，其指数和为 1。第三个平衡点是鞍点，第 2 个、第 1 个是源和汇。系统形成了一个流形上的极限环。

事实上，上述方法是经济学中一般均衡研究的前沿。而该向量场，就被称为 “看不见的手”，引导着我们去追寻那个“一般” 均衡点（市场出清）。

【Ch2. 最优化理论】
这里主要还是总结非线性规划。非线性规划的核心在于 Kuhn-Tucker 定理。这个定理直观的几何图景就是: 目标函数（包括泛函!）水平集的梯度应当与约束流形的切空间垂直。为了保证约束条件可以构成一个光滑流形（从而有切空间）而非其他什么乱七八糟的拓扑流形，我们要求约束条件应当满足约束规范，即所谓的 Jacobi 矩阵满秩。

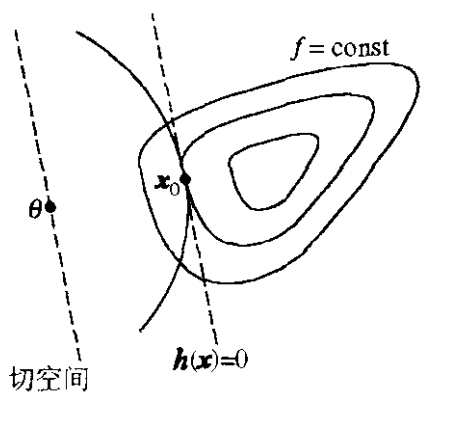
值得一提的是，Kuhn-Tucker 定理对于泛函依旧是成立的。为什么？问题的关键在于分离超平面定理在无穷维线性空间也是成立的!（也即所谓的 Hahn-Banach 定理，泛函分析的基石之一），其次的原因就是泛函分析中的 Frechet 微分保留了几乎所有初等微分学中我们熟悉的性质（链式法则与隐函数定理）。

下面列举一个将 Kuhn-Tucker 定理应用于无穷维空间非线性规划的例子。（读硕士时的笔记）

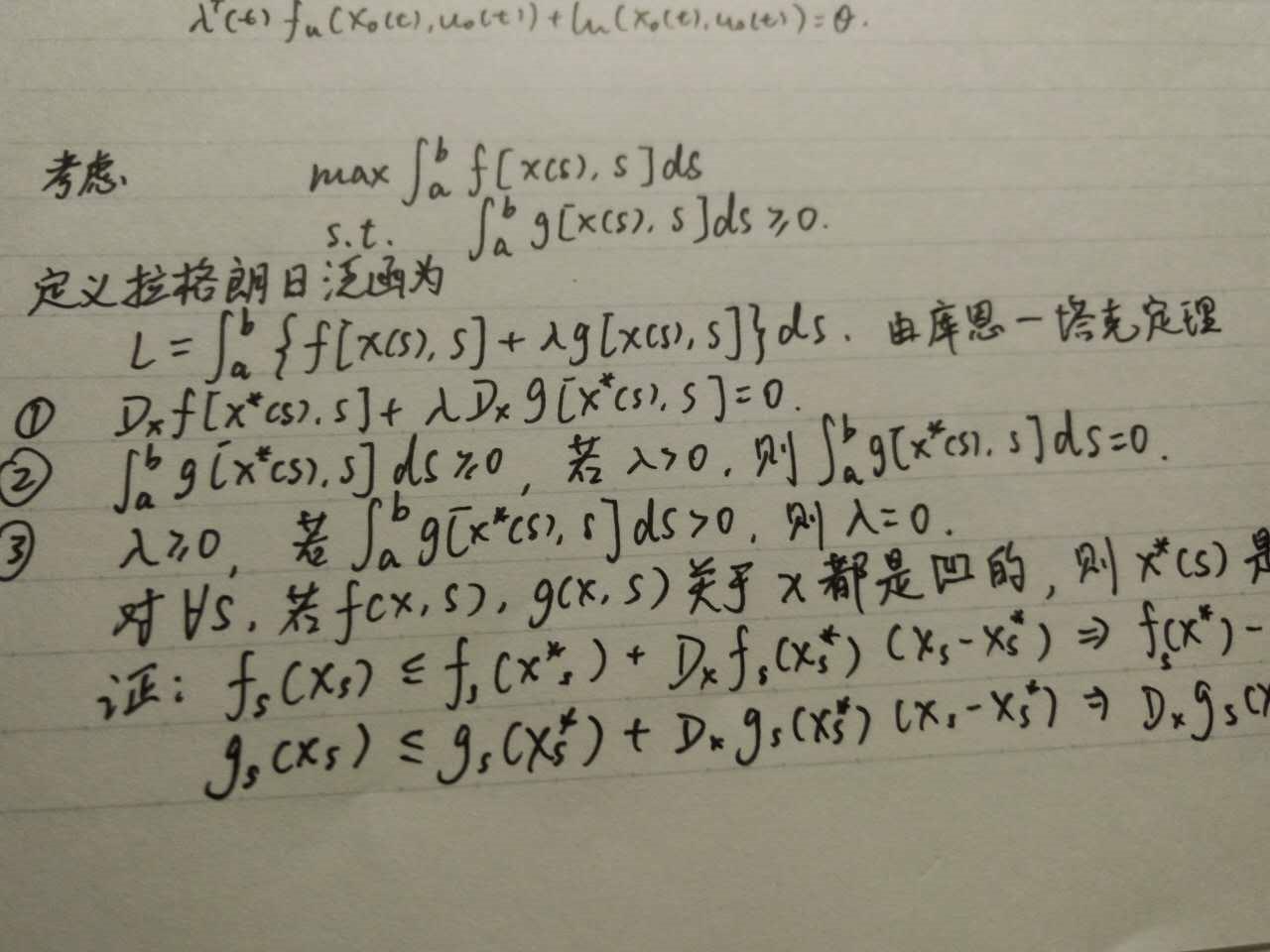
Kuhn-tucker 条件就是 1、2、3，与有限维非线性规划一样。

当然我们可以将它运用到随机优化中，只要注意到数学期望是一个积分算子。

对于最优控制的泛函理论，我会专门另立文章加以阐述。这是一类特殊的变分问题。分段连续最优控制需要泛函分析的对偶空间理论以及 Frechet 微分、无限维空间的反函数定理。

【Ch3. 拓扑方法】

这块内容比较高深，但也算不上艰深。面对许多算子方程（比如系统建模中经常遇到的微分方程、积分方程、随机动态规划的基本方程: Bellman 方程等，还有在非线性动态系统中，研究周期轨道，我们需要面对著名的 Poincare 映射），我们需要确定其解的存在性或者研究映射的不动点。

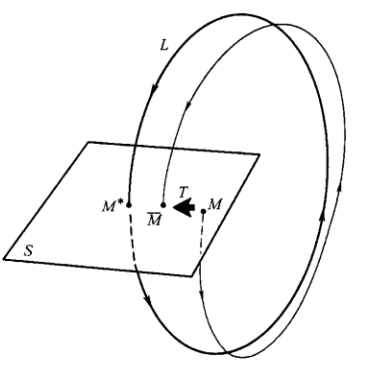
上图是 Poincare 映射的一个例子。讨论周期轨道，我们选取一个超曲面与相轨迹横截，通过一次次回路，我们在截面打出一个个交点——形成一个离散动力系统。这个离散动力系统的不动点问题，就等价于周期轨的存在性问题。

拓扑度作为一种研究不动点理论 "奥义" 般的存在，对非线性科学来说，无疑是极为重要的。要证明算子方程 f(x)=p 有解，我们可以 "万象归一" 地总结为证明 deg(f,Ω,p) 不为 0，而证明拓扑度不为 0，最常用的思路有: 1. 与恒等映射同伦，or，2. 与简单的映射同伦，然后计算简单的映射的 Jaboci 行列式即可（根据映射度的定义，如下图）。

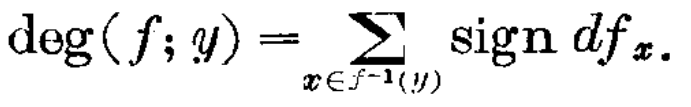
可惜的是，拓扑度在无限维空间中仅对紧算子有用（无奈的摊手）。

对于拓扑度，我们暂时点到为止，因为它可能就是下篇文章——现代变分法与临界点理论的主角之一。

【完】

以上仅仅几例，希望能帮助大家体会现代数学的强大力量。

推荐研读书目，亦是本文参考书目：

1. 米尔诺《从微分观点看拓扑》

2. 艾伯哈特 - 宰德勒《非线性泛函分析及其应用：卷 1，不动点理论》

3. 施尔尼科夫《非线性动力学定性理论方法，卷 1》

对于现代数学的随机部分：随机微分方程理论，知乎上说得已经不少，不再重复。之所以在这里提一下，是因为它也是现代数学的主流之一，更是金融数学的支柱。

写下你的评论...

 

请参考鲁恩伯杰《最优化的矢量空间方法》，从第七章开始到第十章，就是泛函观点下的无限维空间非线性规划和最优控制。这本书被诺贝尔经济学奖得主萨金特赞为 "最优化的圣经"。

膜拜！

谢谢。

虽然看不懂。

数理经济学需要的数学确实不少，如果加上单调算子理论就基本上是非线性泛函分析的几个主要分类了

国际前沿数理经济学基本上代数拓扑、非线性泛函分析都要用到。国内的数理经济学还远远达不到运用非线性泛函分析这个层次。当然，我对非线性泛函分析的理解可能也不如你作为一个数学专业的博士来得透彻。互相学习。

你讲的内容已经包含了 “不动点理论”，“最优化和变分法”

数学本科生献上膝盖。。。

话说文章里面优化部分是哪一门课的内容呀？

请参考鲁恩伯杰《最优化的矢量空间方法》，从第七章开始到第十章，就是泛函观点下的无限维空间非线性规划和最优控制。这本书被诺贝尔经济学奖得主萨金特赞为 "最优化的圣经"。

多谢！

当然还有其他许多内容，我有空会进行扩充。对于现代数学中的随机微分方程，是经济学金融数学专业的拿手好戏。但知乎上这块内容非常多，而过于高深的内容（随机泛函微分方程及其最优控制）受众面太少，遂不考虑添加了。

作为一个仅有高数、线代、概统基础的本科毕业生，需要自学哪些课程才能达到读懂这类问题的门槛？

你想弄懂哪类问题？微分动力系统，还是泛函优化？还是随机微分方程？

如果你感兴趣的是微分动力系统，最快的学习路径是: 先学习一下常微分方程的基本理论，然后就是高等微积分，只需要弄清反函数定理和隐函数定理这两个非线性模型的根基，然后去看杜卡莫《曲线与曲面的微分几何》，只要看第二、三章!（所以说速成嘛），这时候你对常微分方程和光滑流形有一个大概的了解了，就可以开始动力系统的初步研究了。一般数学专业高年级本科生这方面也就学到这里，也即俗称的: 常微分方程定性理论。这时候你应该已经熟悉庞加莱环域定理、稳定流形定理以及 Hartman 线性化定理了。这些定理已经非常强大了。再往后的话，拓扑学就逃不掉了。一旦问题牵扯到拓扑，难度就开始飙升。

请问鲁恩伯杰《最优化的矢量空间方法》这本书的对应英文名是什么，搜了下国内好像没有影印版？

http://m.ishare.iask.sina.com.cn/f/34011191.html

给你找了链接

Hartman Grobman 我记得是 jacobian 矩阵特征值只有虚数部的时候就不能用了，不一定得是零

是的。只有虚部就是非双曲系统

请问关于 Liapunov 函数的这书是谁写的？感觉挺有意思

全文完

本文由 简悦 SimpRead 优化，用以提升阅读体验

使用了 全新的简悦词法分析引擎 ^beta，点击查看详细说明