动态规划法

Posted 2020-12-06 brt2

csdn: 图解算法：动态规划系列

bilibili: 动态规划入门 Introduction to Dynamic Programming

目录

• 1. 适用范围
• 2. 从问题入手
  • 2.1. 爬楼梯
  • 2.2. 最大子序和
  • 2.3. 最长上升子序列
  • 2.4. Coin Change（LintCode-669, 换硬币）
• 3. Unique Paths（LintCode-114, 机器人路径）
• 4. 计算字符串相似度（最优子结构和重叠子问题）

1. 适用范围

题目类型——定性判断：

很多人觉得DP难（下文统称动态规划为DP），根本原因是因为DP区别于一些固定形式的算法（比如DFS、二分法、KMP），没有实际的步骤规定第一步第二步来做什么，所以准确的说，DP其实是一种解决问题的思想。

这种思想的本质是：一个规模比较大的问题（可以用两三个参数表示的问题），可以通过若干规模较小的问题的结果来得到的（通常会寻求到一些特殊的计算逻辑，如求最值等）。

所以我们一般看到的状态转移方程，基本都是这样：

dp[i] = opt(dp[i-1])+1
dp[i][j] = w(i,j,k) + opt(dp[i-1][k])
dp[i][j] = opt(dp[i-1][j] + xi, dp[i][j-1] + yj, ...)

# opt： 指代特殊的计算逻辑，通常为 max() 或 min()
# i,j,k 是在定义DP方程中用到的参数

2. 从问题入手

每一个状态转移方程，多少都有一些细微的差别。这个其实很容易理解，世间的关系多了去了，不可能抽象出完全可以套用的公式。

动态规划的核心，就是找到问题中的状态方程（从复杂问题向更小规模问题的化简过程）。

2.1. 爬楼梯

题目：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定 n 是一个正整数。

示例：

输入：3

输出：3

解释：有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

分析：

• 上 1 阶台阶：有1种方式。
• 上 2 阶台阶：有1+1和2两种方式。
• 上 3 阶台阶：到达第3阶的方法总数就是到第1阶和第2阶的方法数之和。
• 上 n 阶台阶，到达第n阶的方法总数就是到第 (n-1) 阶和第 (n-2) 阶的方法数之和。

我们令 dp[n] 表示能到达第 n 阶的方法总数，可以得到如下状态转移方程：

dp[n] = dp[n-1] + dp[n-2]

代码：

func climbStairs(n int) int {
    if n == 1 {
        return 1
     }
     // 构建状态数组
     dp := make([]int, n+1)
     // 初始状态
     dp[1] = 1
     dp[2] = 2
     // 边界条件
     for i := 3; i <= n; i++ {
         dp[i] = dp[i-1] + dp[i-2]  // 状态方程
    }
    return dp[n]
}

2.2. 最大子序和

题目：

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例 ：

输入: [-2,1,-3,4,-1,2,1,-5,4],

输出: 6

解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

分析：

1. 状态定义：

   dp[i]：表示以 nums[i] 结尾的连续子数组的最大和。

2. 转移方程：

   dp[i] = dp[i-1] + nums[i], if (dp[i-1] >= 0)

   但是这里我们遇到一个问题，很有可能dp[i-1]本身是一个负数。那这种情况的话，如果dp[i]通过dp[i-1]+nums[i]来推导，那么结果其实反而变小了，因为我们dp[i]要求的是最大和。所以在这种情况下，如果dp[i-1]<0，那么dp[i]其实就是nums[i]的值。即

   dp[i] = nums[i] , if (dp[i-1] < 0)

   综上：

   dp[i]=max(nums[i], dp[i?1]+nums[i])

3. 初始状态：

   dp[0] 一定是以 nums[0] 进行结尾，所以

   dp[0] = nums[0]

4. 在很多题目中，因为dp[i]本身就定义成了题目中的问题，所以dp[i]最终就是要的答案。但是这里状态中的定义，并不是题目中要的问题，不能直接返回最后的一个状态 (这一步经常有初学者会摔跟头)。所以最终的答案，其实我们是寻找：

   max(dp[0], dp[1], ..., d[i-1], dp[i])

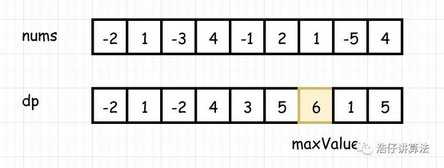
def max_subseq(li):
    # li = [-2,1,-3,4,-1,2,1,-5,4]
    dp = [0] * len(li)
    dp[0] = li[0]

    for i in range(1,len(li)):
        # if dp[i-1] > 0:
        #     dp[i] = dp[i-1] + li[i]
        # else:
        #     dp[i] = li[i]
        dp[i] = max(li[i], dp[i-1] + li[i])

    return max(dp)  # 6

2.3. 最长上升子序列

题目：

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例:

输入: [10,9,2,5,3,7,101,18]

输出: 4

解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

说明:可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。

转移方程：

dp[i] = max(dp[j]+1, dp[k]+1, dp[p]+1, ...)

# 只要满足：

nums[i] > nums[j]
nums[i] > nums[k]
nums[i] > nums[p]
...

代码实现：

def length_LIS(li):
    # li = [10,9,2,5,3,7,101,18]
    dp = [1] * len(li)

    for i in range(1, len(li)):
        curr = li[i]
        for j in range(i):
            if curr > li[j]:
                dp[i] = max(dp[i], dp[j] +1)

    return max(dp)  # 4

2.4. Coin Change（LintCode-669, 换硬币）

求极值

思路：

1. 用一个dp[]来表示状态： dp[x] 表示拼出x所用的最少硬币数

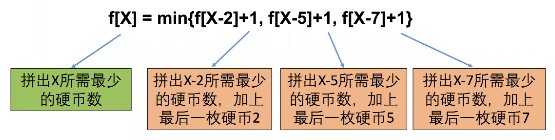
2. 最优策略的最后一步： dp[i] = min(dp[i-2]+1, dp[i-5]+1, dp[i-7]+1)

3. 转移方程

   

4. 初始条件和边界情况（停下来）

def coin_change(x, choices):
    # dp[x] 表示拼出x所用的最少硬币数
    dp = [float("inf")] * (x+1)

    for i in range(1, x+1):
        for j in choices:
            if i == j:
                dp[i] = 1
            elif i > j:
                # dp[i] = min(dp[i-2]+1, dp[i-5]+1, dp[i-7]+1)
                dp[i] = min(dp[i-j]+1 , dp[i])
    # print(dp)
    return dp[x]

3. Unique Paths（LintCode-114, 机器人路径）

4. 计算字符串相似度（最优子结构和重叠子问题）

对于两个字符串A和B，通过基本的增删改将字符串A改成B，或者将B改成A，在改变的过程中我们使用的最少步骤称之为“编辑距离”。

• "A"与"B"的编辑距离很显然是1；
• "A"改成"AB"的编辑距离为1，"A"与"ABA"的编辑距离为2；
• “ABA”和“BBA”的编辑距离为1。