第六章 面试中的各项能力

Posted 2020-12-05 sungc

6.1 面试官谈能力

• 礼貌平和、思路清晰
• 提供解答时观察面试者的沟通能力及求知欲
• 沟通能力、学习能力
• 表达能力
• 是否得到暗示之后迅速做出反应纠正错误
• 是否会在自己得到的信息不够的情况下主动发问澄清

 

6.2 沟通能力和学习能力

• 沟通能力
• 学习能力
• 善于学习、沟通的人也善于提问
• 面试小提示:
• • 面试是一个双向交流的过程，面试官可以问应聘者问题，同样应聘者也可以向面试官提问。如果应聘者能够针对面试题主动地提出几个高质量的问题，面试官就会觉得他有很强的沟通能力和学习能力。

 

6.3 知识迁移能力

• 所谓学习能力，很重要的一点就是根据已经掌握的知识、技术，能够迅速学习、理解新的技术并能运用到实际工作中去。大部分新的技术都不是凭空产生的，而是在已有技术的基础上发展起来的。这就要求我们能够把对已有技术的理解迁移到学习新技术的过程中去，也就是要具备很强的知识迁移能力。

 

面试题38:数字在排序数组中出现的次数

• 题目:统计一个数字在排序数组中出现的次数。例如输入排序数组{1,2,3,3,3,3,4,5}和数字3，由于3在这个数组中出现了4次，因此输出4。
• 思路:利用二分查找+递归思想，进行寻找。当目标值与中间值相等时进行判断
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • System.out.println(t.GetNumberOfK(new int[]{1,2,2,3,3,3,3,4,4,5},3));
  • }
  • public int GetNumberOfK(int[] array, int k) {
  • int result = 0;
  • int mid = array.length / 2;
  • if (array == null || array.length == 0)
  • return 0;
  • if (array.length == 1) {
  • if (array[0] == k)
  • return 1;
  • else
  • return 0;
  • }
  • if (k < array[mid])
  • result += GetNumberOfK(Arrays.copyOfRange(array, 0, mid), k);
  • else if (k > array[mid])
  • result += GetNumberOfK(Arrays.copyOfRange(array, mid, array.length), k);
  • else {
  • for (int i = mid; i < array.length; i++) {
  • if (array[i] == k)
  • result++;
  • else
  • break;
  • }
  • for (int i = mid - 1; i >= 0; i--) {
  • if (array[i] == k)
  • result++;
  • else
  • break;
  • }
  • }
  • return result;
  • }
  • }
• 测试用例:
• • 功能测试(数组中包含查找的数字，数组中没有查找的数字，查找的数字在数组中出现一次/多 次)。
  • 边界值测试(查找数组中的最大值、最小值，数组中只有一个数字)
  • 特殊输入测试(表示数组的指针为NULL指针)。
• 本题考点:
• • 考查应聘者的知识迁移能力。我们都知道二分查找算法可以用来在排序数组中查找一一个数字。应聘者如果能够运用知识迁移能力，把问题转换成用二分查找算法查找重复数字的第-一个和最后一个,那么这个问题也就解决了一大半。
  • 考查应聘者对二分查找算法的理解程度。这道题实际上是二分查找算法的加强版。只有对二分查找算法有着深刻的理解，应聘者才有可能解决这个问题。

 

面试题39:二叉树的深度

• 题目一:输入一棵二叉树的根结点，求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径，最长路径的长度为树的深度。
• 思路:利用递归遍历分别返回左右子树深度
• 代码实现
• • class TreeNode {
  • public int val;
  • public TreeNode left;
  • public TreeNode right;
  • public TreeNode(int val) {
  • this.val = val;
  • }
  • public TreeNode() {
  • }
  • }
  • public class TestTree {
  • public static int n;
  • ArrayList<ArrayList<Integer>> resultList = new ArrayList<ArrayList<Integer>>();
  • ArrayList<Integer> list = new ArrayList<Integer>();
  • public static void main(String[] args) {
  • int[] array = new int[] { 10, 5, 4, 0, 0, 7, 1,0,0,0, 0, 12, 0, 0 };
  • TestTree t = new TestTree();
  • TreeNode root = t.CreateTreeBinary(new TreeNode(), array);
  • System.out.println(t.TreeDepth(root));
  • }
  • public TreeNode CreateTreeBinary(TreeNode treeNode, int[] array) {
  • if (array[n] == 0) {
  • n++;
  • return null;
  • } else {
  • treeNode.val = array[n++];
  • treeNode.left = CreateTreeBinary(new TreeNode(0), array);
  • treeNode.right = CreateTreeBinary(new TreeNode(0), array);
  • return treeNode;
  • }
  • }
  • public int TreeDepth(TreeNode root) {
  • if (root == null)
  • return 0;
  • int left = TreeDepth(root.left);
  • int right = TreeDepth(root.right);
  • return left > right ? left + 1 : right + 1;
  • }
  • }
• 测试用例:
• • 功能测试(输入普通的二叉树，二叉树中所有结点都没有左/右子树)。
  • 特殊输入测试(二叉树只有一一个结点，二叉树的头结点为NULL指针)。
• 题目二:输入一棵二叉树的根结点，判断该树是不是平衡二叉树。如果某二叉树中任意结点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。例如，图6.1中的二叉树就是一棵平衡二叉树。
• 思路:平衡因子的绝对值<= 1.
• 代码实现
• • class TreeNode {
  • public int val;
  • public TreeNode left;
  • public TreeNode right;
  • public TreeNode(int val) {
  • this.val = val;
  • }
  • public TreeNode() {
  • }
  • }
  • public class TestTree {
  • public static int n;
  • ArrayList<ArrayList<Integer>> resultList = new ArrayList<ArrayList<Integer>>();
  • ArrayList<Integer> list = new ArrayList<Integer>();
  • public static void main(String[] args) {
  • int[] array = new int[] { 7, 4, 5, 6, 0, 0, 0, 0, 8, 0, 9, 0, 10, 0, 0 };
  • TestTree t = new TestTree();
  • TreeNode root = t.CreateTreeBinary(new TreeNode(), array);
  • System.out.println(t.IsBalanced_Solution(root));
  • }
  • public TreeNode CreateTreeBinary(TreeNode treeNode, int[] array) {
  • if (array[n] == 0) {
  • n++;
  • return null;
  • } else {
  • treeNode.val = array[n++];
  • treeNode.left = CreateTreeBinary(new TreeNode(0), array);
  • treeNode.right = CreateTreeBinary(new TreeNode(0), array);
  • return treeNode;
  • }
  • }
  • private boolean isBalanced = true;
  • public boolean IsBalanced_Solution(TreeNode root) {
  • getDepth(root);
  • return isBalanced;
  • }
  • public int getDepth(TreeNode root) {
  • if (root == null)
  • return 0;
  • int left = getDepth(root.left);
  • int right = getDepth(root.right);
  • System.out.print(" root: " + root.val);
  • System.out.print(" Math.abs(left - right): " + Math.abs(left - right));
  • System.out.print(" left: " + left);
  • System.out.println(" right: " + right);
  • if (Math.abs(left - right) > 1) {
  • isBalanced = false;
  • }
  • return right > left ? right + 1 : left + 1;
  • }
  • }
• 测试用例:
• • 功能测试(平衡的二叉树，不是平衡的二叉树，二叉树中所有结点都没有左/右子树)。
  • 特殊输入测试(二叉树中只有一一个结点，二叉树的头结点为NULL指针)。
• 本题考点:
• • 考查对二叉树的理解及编程能力。这两个题的解法实际都只是树的遍历算法的应用。
  • 考查对新概念的学习能力。面试官提出一个新的概念即树的深度，这就要求我们在较短的时间内理解这个概念并解决相关的问题。这是一种常见的面试题型。能在较短时间内掌握、理解新概念的能力，就是一种学习能力。
  • 考查知识迁移的能力。如果面试官先问如何求二叉树的深度，再问如何判断一棵=二叉树是不是平衡的，应聘者应该从求二叉树深度的分析过程中得到启发，找到判断平衡二叉树的突破口。

 

面试题40:数组中只出现一次的数字

• 题目:一个整型数组里除了两个数字之外，其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n), 空间复杂度是O(1)。
• 思路:我们还是从头到尾依次异或数组中的每-一个数字，那么最终得到的结果就是两个只出现一次的数字的异或结果。因为其他数字都出现了两次，在异或中全部抵消了。由于这两个数字肯定不一-样，那么异或的结果肯定不为0,也就是说在这个结果数字的二进制表示中至少就有一位为1。我们在结果数字中找到第-一个为1的位的位置，记为第n位。现在我们以第n位是不是1为标准把原数组中的数字分成两个子数组，第-一个子数组中每个数字的第n位都是1,而第二个子数组中每个数字的第n位都是0。由于我们分组的标准是数字中的某一位是1还是0,那么出现了两次的数字肯定被分配到同一个子数组。因为两个相同的数字的任意-一位都是相同的，我们不可能把两个相同的数字分配到两个子数组中去，于是我们已经把原数组分成了两个子数组，每个子数组都包含-一个只出现一次的数字， 而其他数字都出现了两次。我们已经知道如何在数组中找出唯一一个只出现一次数字，因此到此为止所有的问题都已经解决了。
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • t.FindNumsAppearOnce(new int[] {2,4,3,6,2,3,5,5 });
  • System.out.println(t.num1);
  • System.out.println(t.num2);
  • }
  • private int num1;
  • private int num2;
  • public void FindNumsAppearOnce(int[] array) {
  • if (array == null)
  • return;
  • num1 = 0;
  • num2 = 0;
  • int number = array[0];
  • for (int i = 1; i < array.length; i++)
  • number ^= array[i];
  • // 异或后的数1出现在第几位
  • int index = 0;
  • while ((number & 1) == 0) {
  • number = number >> 1;
  • index++;
  • }
  • for (int i = 0; i < array.length; i++) {
  • // 判断第index位是不是0
  • boolean isBit = ((array[i] >> index) & 1) == 0;
  • if (isBit) {
  • num1 ^= array[i];
  • } else {
  • num2 ^= array[i];
  • }
  • }
  • }
  • }

 

• 测试用例:
• • 功能测试(数组中多对重复的数字，数组中没有重复的数字)
• 本题考点:
• • 考查知识迁移能力。只有一个数字出现一-次这个简单的问题，很多应聘者都能想到解决办法。能不能把解决简单问题的思路迁移到复杂问题上，是应聘者能否通过这轮面试的关键。
  • 考查对二进制和位运算的理解。

 

面试题41: 和为 s 的两个数字 VS 和为 s 的连续正数序列

• 题目一:输入一个递增排序的数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，输出任意一对即可。
• 思路:定义两个指针，分别从前面和后面进行遍历。间隔越远乘积越小，所以是最先出现的两个数乘积最小
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • int[] array = new int[] { 2, 4, 5, 7, 8 };
  • System.out.println(t.FindNumbersWithSum(array, 11));
  • }
  • public ArrayList<Integer> FindNumbersWithSum(int[] array, int sum) {
  • ArrayList<Integer> list = new ArrayList<>();
  • if (array == null)
  • return list;
  • int left = 0;
  • int right = array.length - 1;
  • while (left < right) {
  • int s = array[left] + array[right];
  • if (s == sum) {
  • list.add(array[left]);
  • list.add(array[right]);
  • return list;
  • } else {
  • if (s > sum) {
  • right--;
  • } else {
  • left++;
  • }
  • }
  • }
  • return list;
  • }
  • }
• 测试用例:
• • 功能测试(数组中存在和为s的两个数，数组中不存在和为s的两个数)
  • 特殊输入测试(表示数组的指针为NULL指针)

 

• 题目二:输入一个正数s，打印出所有和为s的连续正数序列(至少含有两个数)。例如输入15，由于1+2+3+4+5-4+5+6=7+8=15, 所以结果打印出3个连续序列1~5、4~6和7~8。
• 思路:定义两个指针，分别递增，寻找和为s的序列。
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • int[] array = new int[] { 2, 4, 5, 7, 8 };
  • System.out.println(t.FindContinuousSequence(9));
  • }
  • public ArrayList<ArrayList<Integer>> FindContinuousSequence(int sum) {
  • ArrayList<ArrayList<Integer>> arrayList = new ArrayList<>();
  • ArrayList<Integer> list = new ArrayList<>();
  • if (sum < 3)
  • return arrayList;
  • int small = 1;
  • int big = 2;
  • while (small < (sum + 1) / 2) {//10的时候small到5以后就没有意义了
  • int s = 0;
  • for (int i = small; i <= big; i++) {
  • s += i;
  • }
  • if (s == sum) {
  • for (int i = small; i <= big; i++) {
  • list.add(i);
  • }
  • arrayList.add(new ArrayList<>(list));
  • list.clear();
  • small++;
  • } else {
  • if (s > sum) {
  • small++;
  • } else {
  • big++;
  • }
  • }
  • }
  • return arrayList;
  • }
  • }
• 测试用例:
• • 功能测试(存在和为s的连续序列，如9、100等;不存在和为s的连续序列，如4、0)。
  • 边界值测试(连续序列的最小和3)
• 本题考点:
• • 考查思考复杂问题的思维能力。应聘者如果能够通过一两个具体的例子找到规律，解决这个问题就容易多了。
  • 考查知识迁移的能力。应聘者面对第二个问题的时候，能不能把解决第一个问题的思路应用到新的题目上，是面试官考查知识迁移能力的重要指标。

 

面试题42:翻转单词顺序 VS 左旋转字符串

• 题目一:输入一个英文句子，翻转句子中单词的顺序，但单词内字符的顺序不变。为简单起见，标点符号和普通字母一样处理。例如输入字符串"I am a student.”，则输 出"student. a am I”。
• 思路:先将整个字符串翻转，然后将每个单词翻转。
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • int[] array = new int[] { 2, 4, 5, 7, 8 };
  • System.out.println(t.ReverseSentence("I am a student"));
  • }
  • public String ReverseSentence(String str) {
  • if (str == null || str.length() == 0)
  • return str;
  • if (str.trim().length() == 0)
  • return str;
  • StringBuilder sb = new StringBuilder();
  • String re = reverse(str);
  • String[] s = re.split(" ");
  • for (int i = 0; i < s.length; i++) {
  • sb.append(reverse(s[i]) + " ");
  • }
  • return String.valueOf(sb);
  • }
  • public String reverse(String str) {
  • StringBuilder sb = new StringBuilder();
  • for (int i = str.length() - 1; i >= 0; i--) {
  • sb.append(str.charAt(i));
  • }
  • return String.valueOf(sb);
  • }
  • }
• 测试用例:
• • 功能测试(句子中有多个单词，句子中只有-一个单词)。
  • 特殊输入测试(字符串指针为NULL指针、字符串的内容为空、字符串中只有空格)。
• 题目二:字符串的左旋转操作是把字符串前面的若千个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如输入字符串"abcdefg"和数字2，该函数将返回左旋转2位得到的结果"cdefgab"。
• 思路:拼接或反转三次字符串
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • int[] array = new int[] { 2, 4, 5, 7, 8 };
  • System.out.println(t.LeftRotateString("Iamastudent",5));
  • }
  • public String LeftRotateString(String str,int n) {
  •       if (str == null || str.length() == 0 || n >= str.length())
  •           return str;
  •       String s1 = reverse(str.substring(0,n));
  •       String s2 = reverse(str.substring(n,str.length()));
  •       return reverse(s2)+reverse(s1);
  • }
  • public String reverse(String str) {
  • StringBuilder sb = new StringBuilder();
  • for (int i = str.length() - 1; i >= 0; i--) {
  • sb.append(str.charAt(i));
  • }
  • return String.valueOf(sb);
  • }
  • }
• 测试用例:
• • 功能测试(把长度为n的字符串左旋转0个字符、1 个字符、2个字符、n-1个字符、n个字符、n+1个字符)。
  • 特殊输入测试(字符串的指针为NULL指针)。
• 本题考点:
• • 考查知识迁移的能力。当面试的时候遇到第二个问题，而之前我们做过“翻转句子中单词的顺序”这个题目，那如果能够把多次翻转字符串的思路迁移过来，就能很轻易地解决字符串左旋转的问题。
  • 考查对字符串的编程能力。

 

6.4 抽象建模能力

• 计算机只是一种工具，它的作用是用来解决实际生产生活中的问题。程序员的工作就是把各种现实问题抽象成数学模型并用计算机的编程语言表达出来，因此有些面试官喜欢从日常生活中抽取提炼出问题考查应聘者是否能建立数学模型并解决问题。要想顺利解决这种类型的问题，应聘者除了需要具备扎实的数学基础和编程能力之外，还需要具有敏锐的洞察力和丰富的想象力。
• 建模的第一步是选择合理的数据结构来表述问题。实际生产生活中的问题千变万化，而常用的数据结构却只有有限的几种。我们在根据问题的特点综合考虑性能、编程难度等因素之后，选择最合适的数据结构来表达问题，也就是建立模型。比如在面试题44“扑克牌的顺子”中，我们用一个数组表示-副牌，用11、12和13分别表示J、Q、K并且用0表示大小王。在面试题45“圆圈中最后剩下的数字”中，我们可以用一个环形链表模拟一个圆圈。
• 建模的第二步是分析模型中的内在规律，并用编程语言表述这种规律。我们只有对现实问题进行深入细微的观察分析之后，才能找到模型中的规律，才有可能编程解决问题。例如在本书2.4.2节提到的“青蛙跳台阶”问题中，它内在的规律是斐波那契数列。再比如面试题43“n个骰子的点数”问题，其本质是求数列f(n)=f(n- 1)+f(n- 2)+f(n-3)+f(n-4)+f{n -5)+{(n-6)。找到这个规律之后，我们就可以分别用递归和循环两种不同的方法去写代码。然而，并不是所有问题的内在规律都是显而易见的。在面试题45“圆圈中最后剩下的数字”中，我们经过严密的数学分析之后才能找到每次从圆圈中删除的数字的规律，从而找到一一种不需要辅助环形链表的快速方法来解决问题。

 

面试题43: n个骰子的点数

• 题目:把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。
• 思路:动态规划法求解过程可以使用递归来实现，也可以使用迭代来实现。递归的优势就是代码简洁明了，但是递归有时会对不同阶段的子问题重复求解，所以效率低于迭代。
• 解题思路：
• • 第一步，确定问题解的表达式。可将f(n, s) 表示n个骰子点数的和为s的排列情况总数。
  • 第二步，确定状态转移方程。n个骰子点数和为s的种类数只与n-1个骰子的和有关。因为一个骰子有六个点数，那么第n个骰子可能出现1到6的点数。所以第n个骰子点数为1的话，f(n,s)=f(n-1,s-1)，当第n个骰子点数为2的话，f(n,s)=f(n-1,s-2)，…，依次类推。在n-1个骰子的基础上，再增加一个骰子出现点数和为s的结果只有这6种情况！那么有：
  • f(n,s)=f(n-1,s-1)+f(n-1,s-2)+f(n-1,s-3)+f(n-1,s-4)+f(n-1,s-5)+f(n-1,s-6) ，0< n<=6n
  • f(n,s)=0, s< n or s>6n
  • 上面就是状态转移方程，已知初始阶段的解为：
  • 当n=1时, f(1,1)=f(1,2)=f(1,3)=f(1,4)=f(1,5)=f(1,6)=1。
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • int n = 3;
  • for(int i=n;i<=6*n;++i){
  •             System.out.println(i+" "+t.getNSumCount(n,i));
  • }
  • }
  • public int getNSumCount(int n, int sum) {
  • if (n < 1 || sum < n || sum > 6 * n) {
  • return 0;
  • }
  • if (n == 1) {
  • return 1;
  • }
  • int resCount = 0;
  • resCount = getNSumCount(n - 1, sum - 1) + getNSumCount(n - 1, sum - 2) + getNSumCount(n - 1, sum - 3)
  • + getNSumCount(n - 1, sum - 4) + getNSumCount(n - 1, sum - 5) + getNSumCount(n - 1, sum - 6);
  • return resCount;
  • }
  • }
• 测试用例:
• • 功能测试(1、2、3、4个骰子的各点数的概率)。
  • 特殊输入测试(输入0)。
  • 性能测试(输入较大的数字，比如11)。
• 本题考点:
• • 数学建模的能力。不管采用哪种思路解决问题，我们都要先想到用数组来存放n个骰子的每一个点数出现的次数，并通过分析点数的规律建立模型并最终找到解决方案。
  • 考查对递归和循环的性能的理解。

 

 

面试题44:扑克牌的顺子

• 题目:从扑克牌中随机抽5张牌，判断是不是一个顺子，即这5张牌是不是连续的。2~10为数字本身，A为1，J为11，Q为12，K为13，而大、小王可以看成任意数字。 0为大小王。
• 思路:用数组记录五张扑克牌，将数组调整为有序的，若0出现的次数>=顺子的差值，即为顺子。如果有对子直接返回false。
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • System.out.println(t.isContinuous(new int[]{1,0,3,4,3,0}));
  • }
  • public boolean isContinuous(int[] numbers) {
  • if (numbers == null || numbers.length == 0)
  • return false;
  • int count = 0;
  • int diff = 0;
  • Arrays.sort(numbers);
  • for (int i = 0; i < numbers.length - 1; i++) {
  • if (numbers[i] == 0) {
  • count++;
  • continue;
  • }
  • if (numbers[i] != numbers[i + 1]) {
  • diff += numbers[i + 1] - numbers[i] - 1;
  • } else {
  • return false;
  • }
  • }
  • if (diff <= count)
  • return true;
  • return false;
  • }
  • }
• 测试用例:
• • 功能测试(抽出的牌中有一个或者多个大、小王，抽出的牌中没有大、小王，抽出的牌中有对子)。
  • 特殊输入测试(输入NULL指针)。
• 本题考点:
• • 考查抽象建模能力。这个题目要求我们把熟悉的扑克牌转换为数组，把找顺子的过程通过排序、计数等步骤实现。这些都是把生活中的模型用程序语言来表达的例子。

 

面试题45:圆圈中最后剩下的数字

• 题目: 0,1...,n-1这n个数字排成一个圆圈，从数字0开始每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
• 

   

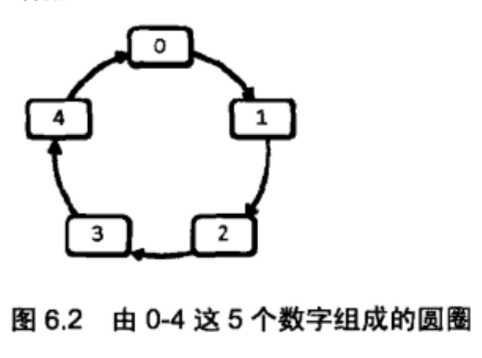
• 思路一:利用循环链表实现
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • System.out.println(t.LastRemaining_Solution(5, 3));
  • }
  • public int LastRemaining_Solution(int n, int m) {
  • LinkedList<Integer> list = new LinkedList<Integer>();
  • int bt = 0;
  • for (int i = 0; i < n; i++) {
  • list.add(i);
  • }
  • while (list.size() > 1) {
  • bt = (bt + m - 1) % list.size();
  • list.remove(bt);
  • }
  • return list.get(0);
  • }
  • }
• 思路二:求出公式，递归计算
• • 

     

• 代码实现
• • public int LastRemaining(int n, int m) {
  • if (n < 1 || m < 1)
  • return -1;
  • int last = 0;
  • for (int i = 2; i <= n; i++)
  • last = (last + m) % i;
  • return last;
  • }
• 测试用例:
• • 功能测试(输入的m小于n,比如从最初有5个数字的圆圈删除每次第2、3个数字;输入的m大于或者等于n，比如从最初有6个数字的圆圈删除每次第6、7个数字)。
  • 特殊输入测试(圆圈中有0个数字)。
  • 性能测试(从最初有4000个数字的圆圈中每次删除第997个数字)。
• 本题考点:
• • 考查抽象建模的能力。不管应聘者是用环形链表来模拟圆圈，还是分析被删除数字的规律，都要深刻理解这个问题的特点并编程实现自己的解决方案。
  • 考查对环形链表的理解及应用能力。大部分面试官只要求应聘者基于环形链表的方法解决这个问题。
  • 考查数学功底及逻辑思维能力。少数对算法和数学基础要求很高的公司，面试官会要求应聘者不能使用O(n)的辅助内存，这个时候应聘者就只能静下心来一步步推导出每次删除的数字有哪些规律。

 

6.5 发散思维能力

    发散思维的特点是思维活动的多向性和变通性，也就是我们在思考问题时注重运用多思路、多方案、多途径地解决问题。对于同一个问题，我们可以从不同的方向、侧面和层次，采用探索、转换、迁移、组合和分解等方法，提出多种创新的解法。

 

面试题46:求1+2+.*.+n

• 题目:求1+2+**.+n.要求不能使用乘除法、for. while. if else. switch、case等关键字及条件判断语句(A?B:C)。
• 思路:巧用递归(返回值类型为Boolean)
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • System.out.println(t.Sum_Solution(5));
  • }
  • public int Sum_Solution(int n) {
  • int sum = n;
  • boolean result = (n > 0) && ((sum += Sum_Solution(n - 1)) > 0);
  • return sum;
  • }
  • }
• 测试用例:
• • 功能测试(输入5、10 求1+2+**+5和1+2+**+10).
  • 边界值测试(输入0和1)。
• 本题考点:
• • 考查发散思维能力。当习以为常的方法被限制使用的时候，应聘者是否能发挥创造力，打开思路想出新的办法，是能否通过面试的关键所在。
  • 考查知识面的广度和深度。上面提供的几种解法，涉及构造函数、静态变量、虚拟函数、函数指针、模板类型的实例化等知识点。只有深刻理解了相关的概念，才能在需要的时候信手拈来。这就是厚积薄发的过程。

 

面试题47:不用加减乘除做加法

• 题目:写一个函数，求两个整数之和，要求在函数体内不得使用+、-、*、/ 四则运算符号。
• 思路:5的二进制是101，17 的二进制是10001。还是试着把计算分成三步:
• • 第一步各位相加但不计进位，得到的结果是10100 (最后一位两个数都是1,相加的结果是二进制的10。这一步不计进位，因此结果仍然是0);第二步记下进位。在这个例子中只在最后一位相加时产生一个进位，结果是二进制的10;第三步把前两步的结果相加，得到的结果是10110， 转换成十进制正好是22。由此可见三步走的策略对二进制也是适用的。接下来我们试着把二进制的加法用位运算来替代。
  • 第一步不考虑进位对每一位相加。0加0、1加1的结果都0，0加1、1加0的结果都是1。我们注意到，这和异或的结果是一样的。对异或而言，0和0、1和1异或的结果是0，而0和1、1和0的异或结果是1。接着考虑第一步进位，对0加0、0加1、1加0而言，都不会产生进位，只有1加1时，会向前产生一个进位。此时我们可以想象成是两个数先做位与运算，然后再向左移动一位。只有两个数都是1的时候，位与得到的结果是1,其余都是0。第三步把前两个步骤的结果相加。第三步相加的过程依然是重复前面两步，直到不产生进位为止。
• 代码实现
• • public class TestMain {
  • public static void main(String[] args) {
  • TestMain t = new TestMain();
  • System.out.println(t.Add(5, 22));
  • }
  • public int Add(int num1, int num2) {
  • //num2 = ~(num2-1); 减法
  • while (num2 != 0) {
  • // 计算相加结果 不考虑进位
  • int temp = num1 ^ num2;
  • // 计算进位(1+1)
  • num2 = (num1 & num2) << 1;
  • num1 = temp;
  • }
  • return num1;
  • }
  • }
• 测试用例:
• • 输入正数、负数和0。
• 本题考点:
• • 考查发散思维能力。当+、-、*、/运算符都不能使用时，应聘者能不能打开思路想到用位运算做加法,是能否顺利解决这个问题的关键。
  • 考查对二进制和位运算的理解。

 

面试题48: 不能被继承的类

• 实现一个不能被继承的类
• 思路:
• • 1、如果类被final修饰，那么此类不可以被继承。
  • 2、如果类中只有private的构造方法，那么此类不可以被继承。
• 本题考点:
• • 考查发散思维能力。当要求设计一个不能被继承的类时，应聘者要马上从把构造函数定义为私有函数出发去寻找解题方法。

 

6.6 本章小结

    面试是我们展示自己综合素质的时候。除了扎实的编程能力，我们还需要表现自己的沟通能力和学习能力，以及知识迁移能力、抽象建模能力和发散思维能力等方面的综合实力(如图6.3所示)。

                            

 

 

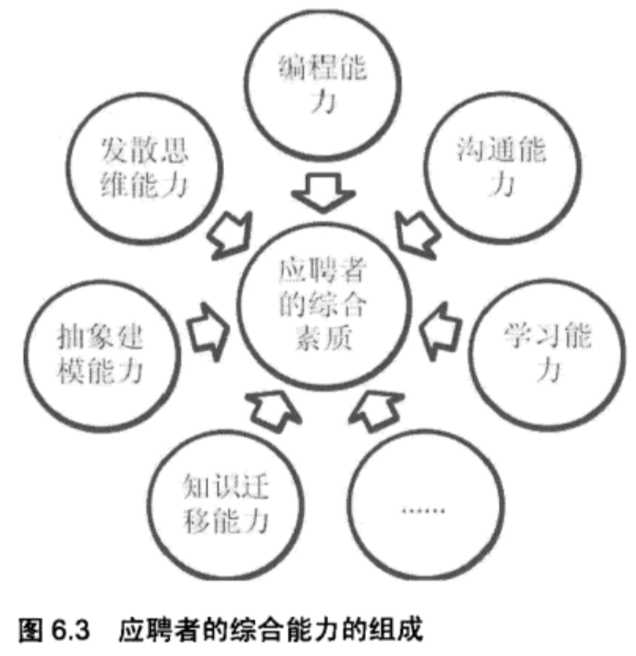
    面试官对沟通能力、学习能力的考查贯穿着面试的始终。面试官不仅会留意我们回答问题时的言语谈吐，还会关注我们是否能抓住问题的本质从而提出有针对性的问题。通常面试官认为善于提问的人有较好的沟通和学习能力。

    知识迁移能力能帮助我们轻松地解决很多问题。有些面试官在提问一道难题之前，会问一道相关但比较简单的题目，他希望我们能够从解决简单问题的过程中受到启发，最终解决较为复杂的问题。另外，我们在面试之前可以做-些练习。如果面试的时候碰到类似的题目，就可以应用之前的方法。这要求我们平时要有一-定的积累，并且每做完-道题之,后都要总结解题方法。

    有一类很有意思的面试题是从日常生活中提炼出来的，面试官用这种类型的问题来考查我们抽象建模的能力。为了解决这种类型的问题，我们先用适当的数据结构表述模型，并分析模型中的内在规律确定计算方法。有些面试官喜欢在面试的时候限制使用常规的思路。这个时候就需要我们充分发挥发散思维的能力，跳出常规思路的束缚，从不同的角度去尝试新的办法。