二叉搜索树的基本操作实现
Posted yiluyisha
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉搜索树的基本操作实现相关的知识,希望对你有一定的参考价值。
1. 二叉搜索树结点结构定义如下:
// 二叉搜索树节点定义
struct TreeNode {
int data;
TreeNode* lChild;
TreeNode* rChild;
TreeNode(int val) : data(val), lChild(NULL), rChild(NULL) {}
};2. 二叉搜索树的基本操作函数如下:
- void preOrderTraverse(TreeNode* head); // 先序遍历(递归)
- TreeNode* searchBST(TreeNode* head, int val); // 查找操作(尾递归)
- TreeNode* iterSearchBST(TreeNode* head, int val); // 查找操作(迭代)
- TreeNode* finMin(TreeNode* head); // 查找最小元素(尾递归)
- TreeNode* finMax(TreeNode* head); // 查找最大元素(迭代)
- TreeNode* insertBST(TreeNode* head, int val); // 插入元素(递归)
- TreeNode* deleteBST(TreeNode* head, int val); // 删除元素(递归)
3. 具体代码实现如下:
#include <iostream>
#include <stack>
using namespace std;
// 二叉搜索树节点定义
struct TreeNode {
int data;
TreeNode* lChild;
TreeNode* rChild;
TreeNode(int val) : data(val), lChild(NULL), rChild(NULL) {}
};
// 先序遍历(递归)
void preOrderTraverse(TreeNode* head) {
if (head) {
cout << head->data << " ";
preOrderTraverse(head->lChild);
preOrderTraverse(head->rChild);
}
}
// 查找操作(尾递归)
TreeNode* searchBST(TreeNode* head, int val) {
if (head == NULL) {
return NULL;
}
if (val > head->data) {
return searchBST(head->rChild, val);
}
else if (val < head->data) {
return searchBST(head->lChild, val);
}
else {
return head;
}
}
// 查找操作(迭代)
TreeNode* iterSearchBST(TreeNode* head, int val) {
TreeNode* node = head;
while (node != NULL) {
if (val > node->data) {
node = node->rChild;
}
else if (val < node->data) {
node = node->lChild;
}
else {
return node;
}
}
return NULL;
}
// 查找最小元素(尾递归)
TreeNode* finMin(TreeNode* head) {
if (head == NULL) {
return NULL;
}
else if (head->lChild == NULL) {
return head;
}
else
return finMin(head->lChild);
}
// 查找最大元素(迭代)
TreeNode* finMax(TreeNode* head) {
TreeNode* node = head;
if (node != NULL) {
while (node->rChild) {
node = node->rChild;
}
}
return node;
}
// 插入元素(递归)
TreeNode* insertBST(TreeNode* head, int val) {
if (head == NULL) {
head = new TreeNode(val);
}
else if (val < head->data) {
head->lChild = insertBST(head->lChild, val);
}
else if (val > head->data) {
head->rChild = insertBST(head->rChild, val);
}
return head;
}
// 删除元素(递归)
TreeNode* deleteBST(TreeNode* head, int val) {
if (head == NULL) {
cout << "The BST is empty. Not find." << endl;
return NULL;
}
else if (val < head->data) {
head->lChild = deleteBST(head->lChild, val);
}
else if (val > head->data) {
head->rChild = deleteBST(head->rChild, val);
}
else if (head->lChild && head->rChild) {
TreeNode* temp = finMin(head->rChild);
head->data = temp->data;
head->rChild = deleteBST(head->rChild, head->data);
}
else {
TreeNode* temp = head;
if (head->lChild == NULL) {
head = head->rChild;
}
else if (head->rChild == NULL) {
head = head->lChild;
}
delete(temp);
}
return head;
}
int main() {
TreeNode* head = NULL;
head = insertBST(head, 3);
head = insertBST(head, 2);
head = insertBST(head, 4);
head = insertBST(head, 1);
head = insertBST(head, 5);
cout << "先序遍历BST元素: " << endl;
preOrderTraverse(head);
cout << endl;
TreeNode* node = NULL;
if (node = searchBST(head, 5)) {
cout << node->data << " is in the BST." << endl;
}
else {
cout << 5 << " is not exist in the BST." << endl;
}
if (node = iterSearchBST(head, 100)) {
cout << node->data << " is in the BST." << endl;
}
else {
cout << 100 << " is not exist in the BST." << endl;
}
if (node = finMin(head)) {
cout << "The minimun element is: " << node->data << "." << endl;
}
if (node = finMax(head)) {
cout << "The maximun element is: " << node->data << "." << endl;
}
head = deleteBST(head, 3);
cout << "Delete " << 3 << ": ";
preOrderTraverse(head);
cout << endl;
head = deleteBST(head, 2);
cout << "Delete " << 2 << ": ";
preOrderTraverse(head);
cout << endl;
system("pause");
return 0;
}4. 运行结果截图如下:
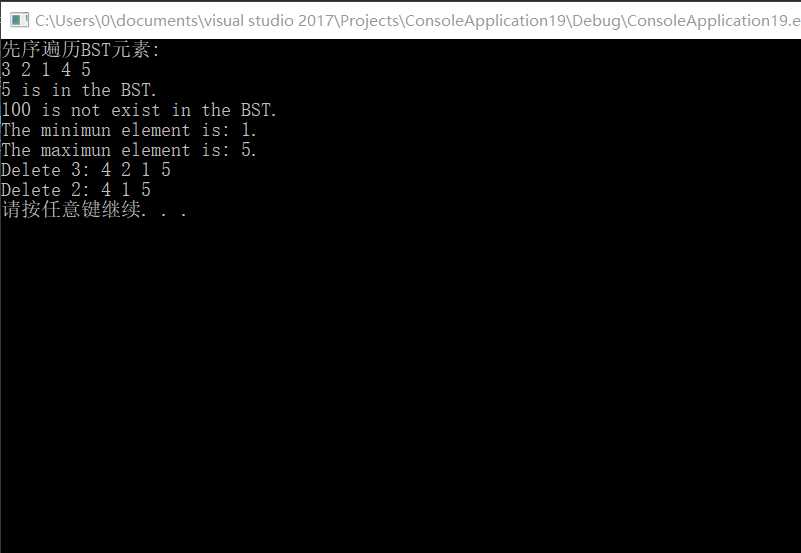
以上是关于二叉搜索树的基本操作实现的主要内容,如果未能解决你的问题,请参考以下文章