题解 POJ3728The merchant（LCA）

Posted 2020-12-04 makerz

题意：一棵树有N个城市，每个城市商品价格不一样，Q个询问，问从u出发到达v点，每个城市只能经过一次的最大利润

max min数组存u城到u的第2^i个祖先路径上的最值

答案就是u-v路径上的最大值-最小值

真的是这样吗？

仔细想想，买入点可能在卖出点之后吗？当然不行

于是把路径分成两段

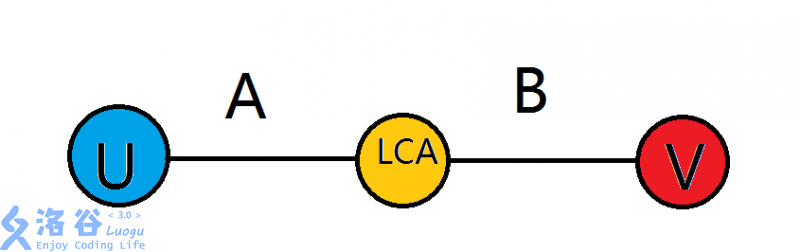
问题就变成下列三种情况

购买和卖出都在A段中完成

购买和卖出都在B段中完成

在A段中购买，B段中卖出

然后将A,B段分别进行处理（感觉像是dp的思想）

这还不够，还要分方向进行处理

shun【u】表示从u往LCA走 dao【u】表示从LCA往u走

最后别忘了处理U-LCA购买，LCA-V卖出的情况

#include<cstdio>
#define inf 0x3f3f3f3f
#define N 50005 

int n,q,a,b;
int cnt;
int val[N],head[N],dep[N];
int f[N][21],mx[N][21],mn[N][21],shun[N][21],dao[N][21];

void inline swap(int &a,int &b){
    a^=b^=a^=b;
}

inline int max(int x,int y){
    if(x>y) return x;
    return y;
}

inline int min(int x,int y){
    if(x<y) return x;
    return y;
}

struct node{
    int v,nex;
}e[N*2];

inline void add(int u,int v){
    cnt++;
    e[cnt].v=v;
    e[cnt].nex=head[u];
    head[u]=cnt;
}
 
inline void dfs(int u,int fa){
    dep[u]=dep[fa]+1;
    f[u][0]=fa;
    mx[u][0]=max(val[u],val[fa]);
    mn[u][0]=min(val[u],val[fa]);
    shun[u][0]=max(0,val[fa]-val[u]);
    dao[u][0]=max(0,val[u]-val[fa]);
    for(register int i=1;i<=20;++i){
        f[u][i]=f[f[u][i-1]][i-1];
        mx[u][i]=max(mx[u][i-1],mx[f[u][i-1]][i-1]);
        mn[u][i]=min(mn[u][i-1],mn[f[u][i-1]][i-1]);
        int k=mx[f[u][i-1]][i-1]-mn[u][i-1];
        int p=mx[u][i-1]-mn[f[u][i-1]][i-1];
        shun[u][i]=max(k,max(shun[u][i-1],shun[f[u][i-1]][i-1]));
        dao[u][i]=max(p,max(dao[u][i-1],dao[f[u][i-1]][i-1]));
    }
    for(register int i=head[u];i;i=e[i].nex){
        int v=e[i].v;
        if(v==fa) continue;
        dfs(v,u);
    }
}

inline int lca(int a,int b){
    int ans=0,Max=0,Min=0x3f3f3f3f;
    Max=val[b],Min=val[a];
    if(dep[a]<dep[b]){
        for(register int i=20;i>=0;--i){
            if(dep[a]>dep[f[b][i]]) continue;
            ans=max(ans,max(Max-mn[b][i],dao[b][i]));
            Max=max(Max,mx[b][i]);
            b=f[b][i];
        }
    }
    else{
        for(register int i=20;i>=0;--i){
            if(dep[b]>dep[f[a][i]]) continue;
            ans=max(ans,max(mx[a][i]-Min,shun[a][i]));
            Min=min(Min,mn[a][i]);
            a=f[a][i];
        }
    }
    if(a==b) return ans;
    for(register int i=20;i>=0;--i){
        if(f[b][i]==f[a][i]) continue;
        ans=max(ans,max(mx[a][i]-Min,shun[a][i]));
        ans=max(ans,max(Max-mn[b][i],dao[b][i]));
        Max=max(Max,mx[b][i]);
        Min=min(Min,mn[a][i]);
        a=f[a][i];
        b=f[b][i];
    }
    ans=max(ans,shun[a][0]);
    ans=max(ans,dao[b][0]);
    Max=max(Max,mx[b][0]);
    Min=min(Min,mn[a][0]);
    ans=max(ans,Max-Min);
    return ans;
}

int main(){
//  freopen("1.in","r",stdin);
//  freopen("E.out","w",stdout);
    scanf("%d",&n);
    for(int i=1;i<=n;++i){
        scanf("%d",&val[i]);
    }
    for(int i=1;i<n;++i){
        scanf("%d%d",&a,&b);
        add(a,b);add(b,a);
    }
    dfs(1,0);
    scanf("%d",&q);
    for(int i=1;i<=q;++i){
        scanf("%d%d",&a,&b);
        printf("%d
",lca(a,b));
    }
    getchar();
    return 0;
}