二分查找（lower_bound和upper_bound）

Posted 2020-12-04 cglongge

　参考自博客：https://www.cnblogs.com/cobbliu/archive/2012/05/21/2512249.html

一直以来对二分查找都是一知半解，终于今天安心的好好学习了一下

　ForwardIter lower_bound(ForwardIter first, ForwardIter last,const _Tp& val)算法返回一个非递减序列[first, last)中的第一个大于等于值val的位置。

    ForwardIter upper_bound(ForwardIter first, ForwardIter last, const _Tp& val)算法返回一个非递减序列[first, last)中第一个大于val的位置。

    lower_bound和upper_bound如下图所示：

 

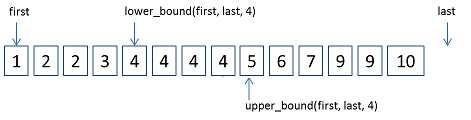
1， lower_bound

　　这个序列中可能会有很多重复的元素，也可能所有的元素都相同，为了充分考虑这种边界条件，STL中的lower_bound算法总体上是才用了二分查找的方法，但是由于是查找序列中的第一个出现的值大于等于val的位置，所以算法要在二分查找的基础上做一些细微的改动。

   以下是我写的二分查找代码

#include<stdio.h>
int s[20];
int lowbound(int l,int r,int k){//求第一个大于等于k的位置 
	int mid;
	int pos;//记录位置 
	while(l<r){
		mid=(l+r)/2;
		if(s[mid]>=k){//因为要求第一个大于等于k的位置，所以当s[mid]==k时，我们要向左找第一个k 
			r=mid;//不能是mid-1，因为可能会到小于k的地方去 
			pos=r;
		}
		else//s[mid]<k时，往右边找第一个等于k的值 
		{
			l=mid+1;
			pos=l;
		}
	}
	return pos;
}
int upbound(int l,int r,int k){//求第一个大于k的位置 
	int mid;
	int pos;//记录位置 
	while(l<r){
		mid=(l+r)/2;
		if(s[mid]<=k){//因为要求第一个大于k的位置，所以当s[mid]<=k时，直接到右边找 
			l=mid+1;
			pos=l;
		}
		else//s[mid]<k时，找第一个大于k的位置，所以r不能等于mid-1，因为mid-1位置上的值可能小于等于k 
		{
			r=mid;
			pos=r;
		}
	}
	return pos;
}
int main(){
	int n;
	int i,j;
	int l,r,k; 
	scanf("%d",&n);
	for(i=1;i<=n;i++){
		scanf("%d",&s[i]);
	}
	char c;
	getchar();
	while(scanf("%c",&c)!=EOF&&c!=‘E‘){
		
		if(c==‘U‘){
			scanf("%d%d%d",&l,&r,&k);
			printf("%d
",upbound(l,r,k));
		}
		else if(c==‘L‘){
			scanf("%d%d%d",&l,&r,&k);
			printf("%d
",lowbound(l,r,k));
		}
		getchar();
	}
	return 0;
}

　　

STL中的实现比较精巧，下面贴出源代码：

下面的代码是STL中的lower_bound实现：

//这个算法中，first是最终要返回的位置
int lower_bound(int *array, int size, int key)
{
    int first = 0, middle;
    int half, len;//len为当前计算数组的长度
    len = size;

    while(len > 0) {
        half = len >> 1;
        middle = first + half;
        if(array[middle] < key) {     
            first = middle + 1;          
            len = len-half-1;       //在右边子序列中查找
        }
        else
            len = half;            //在左边子序列（包含middle）中查找
    }
    return first;
}

下面的代码是STL中的upper_bound实现：

int upper_bound(int *array, int size, int key)
{
    int first = 0, len = size-1;
    int half, middle;

    while(len > 0){
        half = len >> 1;
        middle = first + half;
        if(array[middle] > key)     //中位数大于key,在包含last的左半边序列中查找。
            len = half;
        else{
            first = middle + 1;    //中位数小于等于key,在右半边序列中查找。
            len = len - half - 1;
        }
    }
    return first;
}