RL系列马尔可夫决策过程——状态价值评价与动作价值评价的统一
Posted jinyublog
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了RL系列马尔可夫决策过程——状态价值评价与动作价值评价的统一相关的知识,希望对你有一定的参考价值。
请先阅读上两篇文章:
状态价值函数,顾名思义,就是用于状态价值评价(SVE)的。典型的问题有“格子世界(GridWorld)”游戏(什么是格子世界?可以参考:Dynamic programming in Python),高尔夫游戏,这类问题的本质还是求解最优路径,共性是在学习过程中每一步都会由一个动作产生一个特定的状态,而到达该状态所获得的奖励是固定的,与如何到达,也就是之前的动作是无关的,并且这类问题都有一个或多个固定的目标。相比较而言,虽然Multi-Armed Bandit(MAB)问题也可以用状态价值评价的方法进行policy的求解,不过这个问题本质上还是对动作价值的评价。因为在MAB问题中,一个动作只能产生固定的状态,且一个状态只能由一个固定的动作产生,这种一对一的关系决定了其对动作的评价可以直接转化为状态评价。一个典型的SVE问题在转变为动作价值评价(AVE)问题时(前提是这种转变可行),往往奖励机制会发生变化,从对状态奖励转变为对当前状态的某一动作奖励,因为MAB问题的动作状态等价,所以这种变化并不明显,本篇也就不再将MAB问题作为讨论的例子了。本篇将着重分析一个典型的SVE问题和一个典型的AVE问题,从而引出SVE与AVE在马尔可夫决策过程下的统一形式。这里需要强调一点的是,bellman方程实质上是由AVE的思想引出,与之前我在文章 【RL系列】马尔可夫决策过程与动态编程 中所给出的状态价值评价的推导逻辑还是有些许不同的,所以bellman方程并不适合统一这两种评价体系。如果想要详细了解bellman方程,我认为看书(Reinforcement Learning: An Introduction)和阅读这篇文章 强化学习——值函数和bellman方程 都是不错的选择。
GridWorld
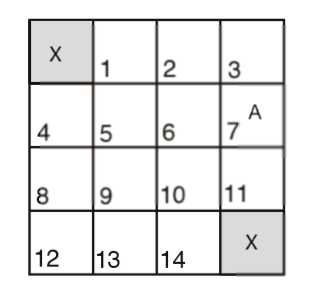
简单介绍一下“格子世界”游戏。这是一个非常简单的寻找最优路劲的问题,给定一个有N*N个网格的地图,在这些网格中有一个或几个目的地,找出地图上任意一个网格到达最近目的地的最短路径。举个例子,如下4x4地图,图中的X即为目的地,A为agent,GridWorld研究的问题就是找到A到达X的最短路径:
以上是关于RL系列马尔可夫决策过程——状态价值评价与动作价值评价的统一的主要内容,如果未能解决你的问题,请参考以下文章