PAT 1146 Topological Order

Posted 2020-12-03 mr-stn

This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

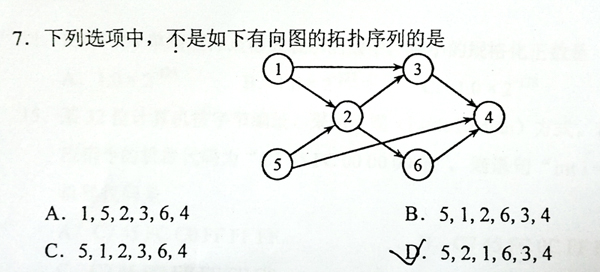
Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:

Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

 

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

Sample Output:

3 4

 1 #include<iostream>
 2 #include<vector>
 3 using namespace std;
 4 int n, k, m;
 5 vector<int> inDegree(1001, 0);
 6 vector< int> Adj[1001], v(1001);
 7 int main(){
 8   int i, j;
 9   cin>>n>>m;
10   for(i=1; i<=m; i++){
11     int v, u;
12     cin>>v>>u;
13     inDegree[u]++;
14     Adj[v].push_back(u);
15   }
16   cin>>k;
17   vector<int> ans;
18   for(i=0; i<k; i++){
19     for(j=0; j<n; j++) cin>>v[j];
20     bool flag=true;
21     vector<int> temp(1001, 0);
22     for(j=0; j<n; j++){
23       if(temp[v[j]]==inDegree[v[j]]){
24         for(int idx=0; idx<Adj[v[j]].size(); idx++) temp[Adj[v[j]][idx]]++;
25       }else{
26         flag = false;
27         break;
28       }
29     }
30     if(!flag) ans.push_back(i);
31   }
32   cout<<ans[0];
33   for(i=1; i<ans.size(); i++) cout<<" "<<ans[i];
34   return 0;
35 }