数据结构前向星存图

Posted 2020-12-02 brokenstring

本文转自acdreamers的博客 原文网址：
https://blog.csdn.net/ACdreamers/article/details/16902023

我们首先来看一下什么是前向星.

前向星是一种特殊的边集数组,我们把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大排序,

并记录下以某个点为起点的所有边在数组中的起始位置和存储长度,那么前向星就构造好了.

用len[i]来记录所有以i为起点的边在数组中的存储长度.

用head[i]记录以i为边集在数组中的第一个存储位置.

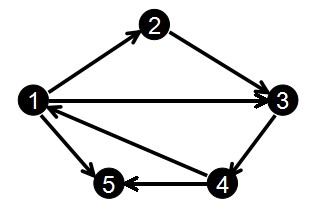
那么对于下图:

我们输入边的顺序为:

1 2

2 3

3 4

1 3

4 1

1 5

4 5

那么排完序后就得到:

编号: 1 2 3 4 5 6 7

起点u: 1 1 1 2 3 4 4

终点v: 2 3 5 3 4 1 5

得到:

head[1] = 1 len[1] = 3

head[2] = 4 len[2] = 1

head[3] = 5 len[3] = 1

head[4] = 6 len[4] = 2

但是利用前向星会有排序操作,如果用快排时间至少为O(nlog(n))

如果用链式前向星,就可以避免排序.

我们建立边结构体为:

struct Edge

{

     int next;

     int to;

     int w;

};

其中edge[i].to表示第i条边的终点,edge[i].next表示与第i条边同起点的下一条边的存储位置,edge[i].w为边权值.

另外还有一个数组head[],它是用来表示以i为起点的第一条边存储的位置,实际上你会发现这里的第一条边存储的位置其实

在以i为起点的所有边的最后输入的那个编号.

head[]数组一般初始化为-1,对于加边的add函数是这样的:

void add(int u,int v,int w)  
{  
    edge[cnt].w = w;  
    edge[cnt].to = v;  
    edge[cnt].next = head[u];  
    head[u] = cnt++;  
}  

初始化cnt = 0,这样,现在我们还是按照上面的图和输入来模拟一下:

edge[0].to = 2; edge[0].next = -1; head[1] = 0;

edge[1].to = 3; edge[1].next = -1; head[2] = 1;

edge[2].to = 4; edge[2],next = -1; head[3] = 2;

edge[3].to = 3; edge[3].next = 0; head[1] = 3;

edge[4].to = 1; edge[4].next = -1; head[4] = 4;

edge[5].to = 5; edge[5].next = 3; head[1] = 5;

edge[6].to = 5; edge[6].next = 4; head[4] = 6;

很明显,head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置.

这样在遍历时是倒着遍历的,也就是说与输入顺序是相反的,不过这样不影响结果的正确性.

比如以上图为例,以节点1为起点的边有3条,它们的编号分别是0,3,5 而head[1] = 5

我们在遍历以u节点为起始位置的所有边的时候是这样的:

for(int i=head[u];~i;i=edge[i].next)

那么就是说先遍历编号为5的边,也就是head[1],然后就是edge[5].next,也就是编号3的边,然后继续edge[3].next,也

就是编号0的边,可以看出是逆序的.

---

样例加深理解

此处非原博客 而是本人添加
例题：洛谷P3371单源最短路径模板
https://www.luogu.org/problemnew/show/P3371
此处运用SPFA+链式前向星

#include<iostream>
using namespace std;
int exist[500010];
int team[2000000];
int dis[500010];
int head[500010];
int n,m,s;
int x,y,z;
int cnt;
int t=0,w=1;
struct edge
{
    int next;
    int to;
    int w;
}edge[2500010];
void add(int u,int v,int w)
{
    edge[++cnt].w=w;
    edge[cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt;
}
int main()
{
    cin>>n>>m>>s;
    for(int i=1;i<=n;i++)
    dis[i]=2147483647;
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y>>z;
        add(x,y,z);
    }
    dis[s]=0;
    team[1]=s;
    while(t<w)
    {
        t++;
        int u=team[t];//u等于入队的点 
        exist[u]=0;
        for(int i=head[u];i!=0;i=edge[i].next)//i从每个点能到的最后一条遍循环到第一条边 
        {
            int v=edge[i].to;//v等于每条遍的后面那个点 
            if(dis[v]>dis[u]+edge[i].w)//如果到这条遍后面的点距离比到这条边前面点加上边的权值小 
            {
                dis[v]=dis[u]+edge[i].w;
                if(!exist[v])
                {
                    w++;
                    exist[v]=1;
                    team[w]=v;
                }
            }
        }
    }
    for(int i=1;i<=n;i++) 
    cout<<dis[i]<<" ";
}