P2045 方格取数加强版

Posted 2020-12-02 caterpillor

将点拆成两条边，一条边的容量是1，费用是a[i],一条边的容量是K-1,费用是0.这样保证了，一个点不超过K次经过，而且第一次经过就将上面的数取走了，再经过就没有数可取了。

一个点要和自己连得方法是，都加一个比较大的数。比如一共n^2个点，那么1节点连向1+n^2,就是自己和自己连边了。

还有个问题开始困扰时间比较长，第一是源点为什么不能就是1,汇点是n^2.

因为这样节点有两条边连接，每条边的容量是K,这样流入节点的容量可以是2*k，那么就不是不超过k次经过了。而是2*k.

这样一来画出来图就是:

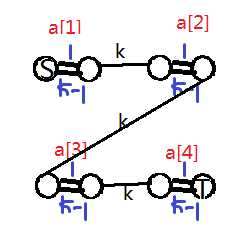
然后就是最低费用最大流问题。

一直re,通常情况下是数组的问题。检查了很久发现，一个点要有4条边，一条是容量是1，另一条是K-1,还有两条反向边。因此，是n^2*4的边数。

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<queue>
#include<cstring>
#define inf 0x3f3f3f3f
using namespace std;
int n,k,ans,hd[6010],cnt=1,a[55][55],flow[6010];
int dis[6010],vis[6010],last[6010];
int s,t,pre[6010];
struct Edge{
    int nxt,to,flw,cos;
}edge[20010];
void add(int u,int v,int w,int f)
{
    cnt++;
    edge[cnt].to=v;
    edge[cnt].flw=w;
    edge[cnt].cos=f;
    edge[cnt].nxt =hd[u];
    hd[u]=cnt;
}
queue<int> q;
int spfa(int s,int t)
{
    memset(dis,0x3f,sizeof dis);
    memset(vis,0,sizeof vis);
    memset(flow,0x3f,sizeof flow);
//    memset(last,0,sizeof last);
    memset(pre,-1,sizeof pre);
    q.push(s);
    vis[s]=1;
    dis[s]=0;
    pre[t]=-1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=hd[u];i;i=edge[i].nxt)
        {
            int v=edge[i].to;
            if(edge[i].flw>0 && dis[v]>dis[u]-edge[i].cos)
            {
                flow[v]=min(flow[u],edge[i].flw);
                dis[v]=dis[u]-edge[i].cos;
                last[v]=i;
                pre[v]=u;
                if(!vis[v])
                {
                    q.push(v);
                    vis[v]=1; 
                }
            }    
        }
        vis[u]=0;
    }
    return pre[t]!=-1;
}
int mxcost=0;
void mcmf()
{
    while(spfa(s,t))
    {
        mxcost+=(-dis[t]);//
        int now=t;
        while(now!=s)
        {
            edge[last[now]].flw-=flow[t];
            edge[last[now]^1].flw+=flow[t];
            now=pre[now];
        }
    }
}
int main()
{
    scanf("%d%d",&n,&k);
    int N=n*n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            int q,p=n*(i-1)+j;
            scanf("%d",&a[i][j]);
            add(p,p+N,1,a[i][j]);//自己连自己
            add(p+N,p,0,-a[i][j]);//反向边 
            add(p,p+N,k-1,0);//另一条边，容量为K-1的，费用为0，保证了K的流量 
            add(p+N,p,0,0);    //反向边 
            if(i-1>0)
            {
                q=n*(i-2)+j+N;//上一行的点的出点 
                add(q,p,k,0);
                add(p,q,0,0);
                //只有出点连边 
            } 
            if(j-1>0)
            {
                add(p-1+N,p,k,0);//左一行的点的出点 
                add(p,p-1+N,0,0);
            }
//            for(int j=hd[p];j;j=edge[j].nxt)
//            {
//                cout<<p<<","<<edge[j].to<<","<<edge[j].flw<<","<<edge[j].cos<<endl;
//            } 
        }
//        for(int u=1;u<=2*n*n;u++)
//            for(int j=hd[u];j;j=edge[j].nxt)
//            {
//                cout<<u<<","<<edge[j].to<<","<<edge[j].flw<<","<<edge[j].cos<<endl;
//             } 
        s=1;t=2*n*n;
        mcmf();
        printf("%d
",mxcost);
}