人工神经网络(初识)

Posted 2020-12-01 ljc-0923

人工神经网络

• 人工神经网络,是模拟生物神经网络进行信息处理的一种数学模型,它对大脑的生理研究成果为基础,其目的在于模拟大脑的某些机理与机制,实现一些特定的功能
• 1943年, 美国心里学家和数学家联合提出了形式神经元的数学模型MP模型,证明了单个神经元能执行逻辑功能,开创了人工神经网络研究的时代.1957年,计算机科学家用硬件完成了最早的神经网络模型,即感知器,并用来模拟生物的感知和学习能力.1969年, M.Minsky等仔细分析了以感知器为代表的神经网络系统的功能及局限后,指出感知器不能解决高阶谓词问题.随着20世纪80年代以后,超大规模集成电路,脑科学,生物学,光学的迅速发展为人工神经网络的发展打下了基础,人工神经网络进入兴盛期
• 人工神经元是人工神经网络操作的基本信息处理单位,人工神经元的模型如下,它是人工神经网络设计基础,一个神经原对输入信号X = [x₁, x₂, ...x_m]^T的输出y为y=f(u+b)
•  
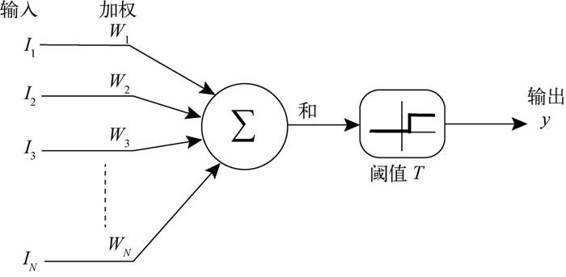
• 人工神经网络的学习也称为训练,指的是神经网络在收到外部环境的刺激下调整神经网络的参数,是神经网络以一种新的方式对外部环境做出反应的一个过程.在分类与预测中,人工神经将网络主要使用有指导的学习方式,即根据给定的训练样本,调整人工神经网络的参数以使网络输出接近于已知的样本类标记或其他形式的因变量.
• 激活函数分类表
• 
• 在人工神经网络的发展过程中,提出了多种努通的学习规则.没有一种特定的学习算法适用于所有的网络的结构和具体问题.在分类与预测中,δ学习规则(误差矫正学习算法)是使用最广泛的一种误差矫正学习算法个努神经网络的输出误差对神经元的连接强敌进行修正,属于有指导的学习.设神经网络中的神经元i作为输入,神经元j作为输出神经元,他们的连接权值为wij,则对权值的修正为Δw_ij = ηδ_iΥ_i,其中η为学习率,δj = Τ_j - Υ_j为j的偏差,即输出神经元j的实际输出和教师信号之差,
• 神经网络训练是否完成常用函数(也是目标函数)E来衡量.当误差函数小于某一个设定的值使即停止神经网络的训练误差函数为衡量实际输出向量Y_k于期望值向量Tk误差大小的函数,长采用二乘误差函数来定义为E = 1/2∑ⁿ_k=1[Υ_k - Τ_k]²n为训练样本的个数
• 使用人工神经网络模型需要确定网络连接的拓扑结构,神经元的特征和学习规则等,常用的用来实现分诶和预测人工神经网络算法如下

• 算法名称	算法描述
  ANFIS自适应神经网络	神经网络镶嵌在一个全部模糊的结果之中,在不知不觉中向训练数据学习,自动生产,修正并高度概括出最佳的输入与输出变量的隶属函数以及模糊规则;另外,神经网络的各层结构于参数也都具有了明确的,易于理解的物理意义.
  BP神经网络	是一种按误差逆传播算法训练的多层前馈网络,学习算法是δ学习规则,是目前应用最广泛的神经网络模型之一
  FNN神经网络	FNN模糊神经网络是具有模糊权系数或者输入信号是模糊量的神经网络,是模糊系统与神经网络项结合的产物,它汇聚了神经网络与模糊系统的优点,集联想,识别,自适应及模糊信息处理于一体.
  GMDH神经网络	GMGH网络也称为多项式网络,它是前馈神经网络中常用的一种用于预测的神经网络,它的特点是网络结构不固定,而且在训练过程中不断改变
  LM神经网络	是基于梯度下降法和牛顿法结合的多层前馈网络,特点:迭代次数少,收敛速度快,精确度高
  RBF径向基神经网络	RBF网络能够以任意精度逼近任意连续函数,从输入层到隐含层的变换是非线性的,而从隐含层到输出层的变换是线性的,特别适合于解决分类问题

• BP神经网络的学习算法是δ学习规则,目标函数采用E = ∑ⁿ_k=1[Y_k - T_k]²
• 反向传播算法的特征是利用输出后的误差来估计输出层的直接前导层的误差,再用这个误差估计更前一层的误差,如此一层一层的反向传播下去,就获得了所有其他各层的误差估计,这样就形成了将输出层表现出的误差沿着与输入传送相反的放线逐级项网络的输入层传递的过程.
• BP算法的学习过程由信号的正向传播与误差的逆向传播两个过程.正向传播时,输入信号胫骨隐层的处理后,传向输出层.若输出节点未能获得期望的输出,则准入误差的逆向传播阶段,将输出误差按某种形式,通过隐层向输入层返回,并分摊给隐层4个节点与输入层x₁, x₂, x₃三个输入节点,从而获得各层单元的参考误差或称号误差,作为修改各单元权值的依据.这种信号正向传播与误差逆向传播的各层权矩阵的修改过程,是周而复始进行的,权值不断修改过程,也就是网络的学习(活称训练)过程.此过程一直进行到网络输出的误差逐渐减少到可接受的程度或达到设定的学习次数为止.
• 算法开始后,给定学习次数上限初始化学习次数为0,对权值和阈值赋予晓得随机数,一般在[-1.1]之间,输入样本数据,网络正向传播,得到中间层与输出层的值.比较输出层的值与教师信号值的误差用误差函数E来判断误差是否小于误差上限,入不小于误差上限,则对中间层和输出层权值和阈值进行更新,更新的算法为δ学习规则,更新权值和阈值后,再次将样本数据作为输入,得到中间层与输出层的值,计算误差E是否小于上限,学习次数是否达到指定值,如达到,学习结束.
•  
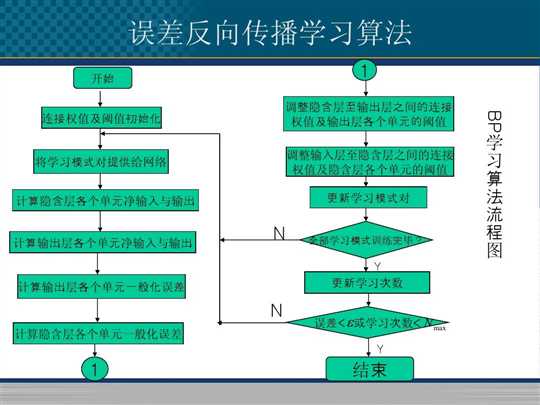
• BP算法只用到均方误差函数对权值和阈值的一阶导数(梯度)的信息,使得算法存在收敛速度缓慢,易陷入局部较小等缺陷.为了解决这一问题,Hinton等人于2006年提出了非监督贪心逐层训练算法,为解决深层结构相关的优化难题带来希望,并以此为基础,发展称了"深度学习"算法,本书中所建立的神经网络,结构跟传统的BP神经网络是类似的,但是求解算法已经用了新的逐层训练算法
• 神经网络预测销量高低代码如下

• # -*- coding:utf-8 -*-
  
  import sys
  
  reload(sys)
  sys.setdefaultencoding("utf-8")
  
  """
  使用神经网络算法预测销量高低
  """
  
  # 参数初始化
  import pandas as pd
  data = pd.read_csv("./sales.csv", header=None, sep="	",
                     names=["date", "sale", "item1", "item2", "item3", "item4"])
  # 根据类别表前转化成数据
  data[data["item1"] == u"好"] = 1
  data[data["item1"] != u"好"] = 0
  
  data[data["item2"] == u"好"] = 1
  data[data["item2"] != u"好"] = 0
  
  data[data["item3"] == u"好"] = 1
  data[data["item3"] != u"好"] = 0
  
  data[data["item4"] == u"好"] = 1
  data[data["item4"] != u"好"] = 0
  
  x = data.iloc[:, :3].as_matrix().astype(int)  # 转化称int
  y = data.iloc[:3].as_matrix().astype(int)  # 转化成int
  
  from keras.models import Sequential
  from keras.layers.core import Dense, Activation
  
  model = Sequential()  # 建立模型
  model.add(Dense(3, 10))
  model.add(Activation(‘relu‘))  # 用relu函数作为激活函数,能够大幅提供精准度
  model.add(Dense(10, 1))
  model.add(Activation(‘sigmoid‘))  # 由于是0-1输出,用sigmoid函数作为激活函数
  
  model.compile(loss=‘binary_crossentropy‘,optimizer=‘adam‘, class_mode=‘binary‘)
  # 编译 模型,由于做的是二元分类,所以指定损失函数为binary_crossentropy,以及模式为binary
  # 另外常见的损失函数还有mean_squared_error,categorical_crossentropy等,
  
  model.fit(x,y, nb_epoch=1000, batch_size=10)  # 训练模型 # 学习1000次
  yp = model.predict_classes(x).reshape(len(y))  # 分类预测

• 神经网络需要较多的样本集,另外哎吆考虑过拟合的情况,事实上,神经网络的拟合能力很强.容易出现果泥喝现象.