第三章动态规划小结

Posted 2020-11-30 snowlxy

动态规划

3.1、矩阵连乘问题

标准算法：

 1 void matrixMultiply（int **a,int **b,int **c,int ra,int ca, int rb,int cb）{
 2     if(ca !=rb)
 3         error("矩阵不可乘")；
 4     for(int i=0;i<ra;i++){
 5         for(int j=0;j<cb;j++){
 6             int sum = a[i][0]*b[0][j];
 7             for(int k=1;k<ca;k++)
 8                 sum+=a[i][k]*b[k][j];
 9             c[i][j] = sum;
10             }
11         }
12 }

矩阵连乘问题的标准算法

动态规划法解法步骤：

①分析最优解的结构：刻画该问题的最优解的结构特征，矩阵连乘积计算次序问题的最优解包含着其子问题的最优解——最优子结构性质。

②建立递归关系

作业题

3-1 单调递增最长子序列 

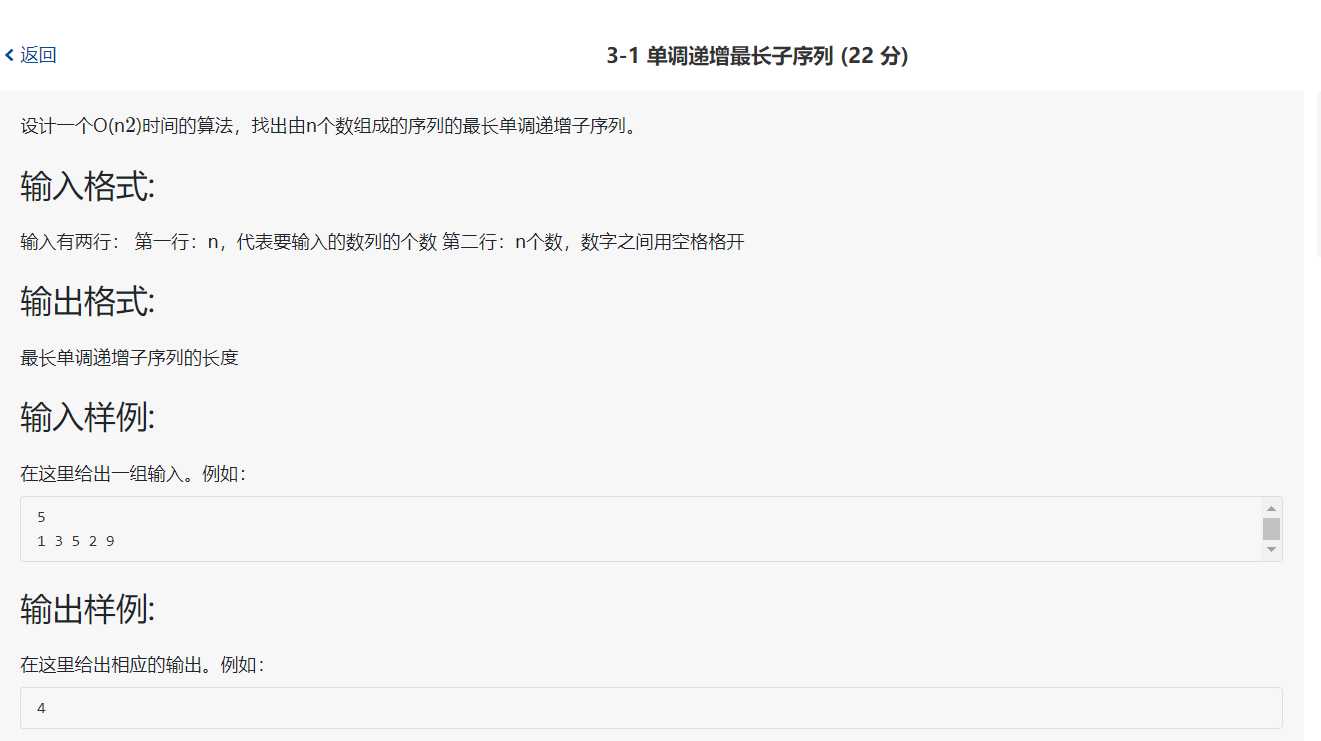
 1 #include<iostream>
 2 using namespace std;
 3 
 4 int main(){
 5     int n;//n个数字
 6     cin >> n;
 7     int a[n];
 8     for(int i=0;i<n;i++){
 9         cin >> a[i];
10     } 
11     
12     int m[n] = {1};
13     int max=0;
14     for(int i=1;i<n;i++){
15         for(int j=0;j<i;j++){
16             if(a[i] > a[j] && m[i] < m[j]+1) {
17                 m[i] = m[j] +1;
18             }
19         }
20     }
21     for(int i=0;i<n;i++){
22         if(max < m[i])
23             max = m[i];
24     }
25     cout << max;
26     return 0;
27 } 

单调递增最长子序列

题目分析：

1.数据结构

①a[n]存放n个数；②bool Islarger[n]用于判断a[i]>a[i-1]为true or false; ③int flag用于标记是否进行过lslarger的判断；④ int length用于存放单调递增序列的长度

2.递归方程  

length = max{a[i]>a[i-1],0}+1 

①由于只有一个数的时候，序列长度为1 ，因此后面加了一个1

②当a[i]>a[i-1]时 为递增，a[i]>a[i-1]返回1，因此max{a[i]>a[i-1]，0}返回1 ，length加一即序列长度加一

　 当a[i]<a[i-1]时 非递增， a[i]<a[i-1]返回-1，因此max{a[i]>a[i-1],0}返回0，length长度不变

 

3-2 租用游艇问题 

 1 #include<iostream>
 2 using namespace std;
 3 
 4 int main(){
 5     int n;
 6     cin >> n;//n个游艇出租站 
 7     int boat_rent[200][200];
 8     int rent[n][n];
 9     for(int i=1;i<=n;i++){
10         boat_rent[i][i]=0;
11     }
12 
13     for(int i=1;i<n;i++){
14         for(int j=i+1;j<=n;j++){
15             cin >> boat_rent[i][j];
16         } 
17     }
18     for(int i=1;i<n;i++){
19         for(int j=i+1;j<=n;j++){
20             rent[i][j] = boat_rent[i][j];
21         }
22     }
23     int  k;
24     for(int i=2;i<=n;i++){//到第i个站点 
25         for(int j=i+1;j<=n;j++){//从每一个站点开始 
26             k = j-i;//r(i,j)长度为j 
27             for(int p=k;p<j;p++){//找出某一站k,使得r(i,k)+r(k,j)最小
28                 if(boat_rent[k][j] > boat_rent[k][p]+boat_rent[p][j])
29                     boat_rent[k][j]=boat_rent[k][p]+boat_rent[p][j];
30             }
31         }
32     }
33     cout << boat_rent[1][n];
34     return 0;
35 }
36  

租用游艇问题

代码分析：

1）数据结构：

①int boat_rent[][]:定义每个出租站到另外一个出租站的租金；②int  k:从中间的站点分开，选择从起始站点到终点最短的距离；③rent[][]将boat_rent重新填入rent[][]

 

 

2)递归函数

rent[1][n] = min{boat_rent[1][k]+boat_rent[k][n],boat_rent[1][n]}

结对编程的汇报情况：

这次结对编程我们写的是数字三角形、最大字段和和编辑距离问题，在课上我们只做出了数字三角形一道题，是利用了直接在表上重新填写的方法，利用了填表法的思想，但是没有另建一个表格。后来在写最大字段和的时候，我们的确卡住了，想要算两个正数之间的和，但是又考虑到重复问题，最后下课了也没有解决这个问题。

而这三道题中，我们觉得最难的是编辑距离问题，在网上查找了之后，依旧没有弄懂，希望老师能讲一下这道题。