曲面细分阶段
Posted chenglixue
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了曲面细分阶段相关的知识,希望对你有一定的参考价值。
什么是曲面细分阶段?
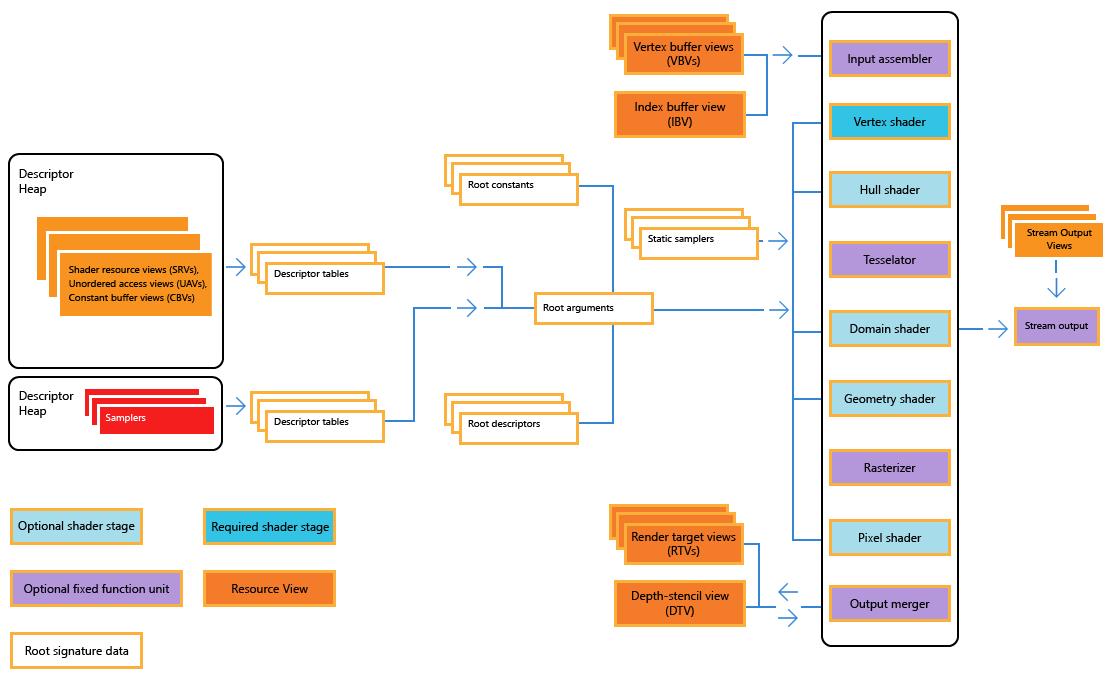
曲面细分(tessellation)阶段是GPU渲染管线中一个可选阶段,在该阶段中又包含三个阶段——外壳着色器(hull shader,HS)阶段、镶嵌器(tessellator)阶段、域着色器(domain shader, GS)阶段.通过使用这三个阶段,我们可以细分几何体,使其拥有更丰富的网格细节,从而使其更加平滑,提高视觉效果
为什么需要曲面细分?
在这里存在一个问题,既然曲面细分是细分几何体,那为什么不在输入装配阶段(IA)直接赋予高模细节呢?原因如下:
-
实现动态LOD(level of detail,细节级别)。根据网格与相机的距离或其他因素来调整细节
比如,若相机离网格远,一般来说玩家并不能注意其细节区别,因此对于当前这种情况来说我们可以降低网格细节来降低开销;而若相机离网格近的话,我们可以丰富网格细节来丰富视觉效果
-
物理模拟和动画特效
在低模网格上执行物理模拟和动画特效的计算,随后再丰富网格细节,以此降低开销
-
节约内存
保存时采用低模网格节省资源,而后再根据需要丰富网格细节
曲面细分的方式
Loop细分
Loop细分是一种针对三角形面的方法,它的细分步骤如下:
-
将一个三角形细分为四个
如下图所示,选定每条边的中点,再挨个相连使得一个三角形细分为四个三角形
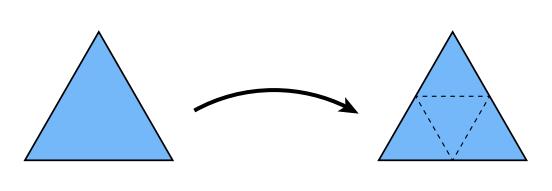
-
根据权重分配新的顶点位置
如下图,为了确定新的顶点位置(白色的顶点),对ABCD四个顶点的
权重求和即可
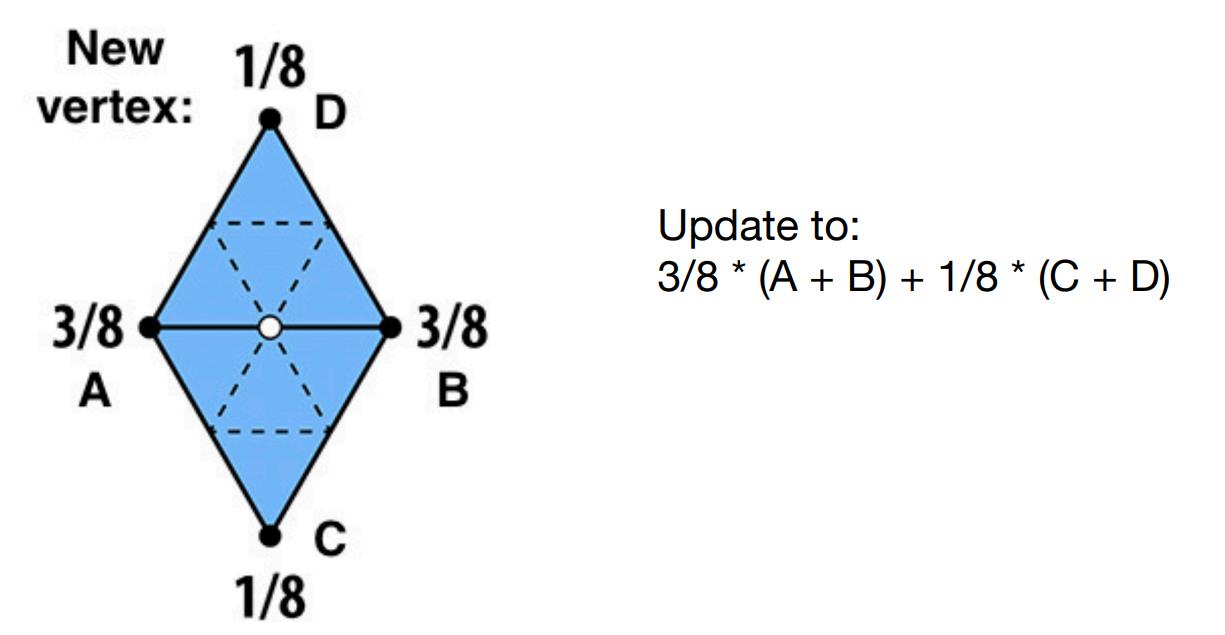
-
根据权重重新设置旧顶点的位置
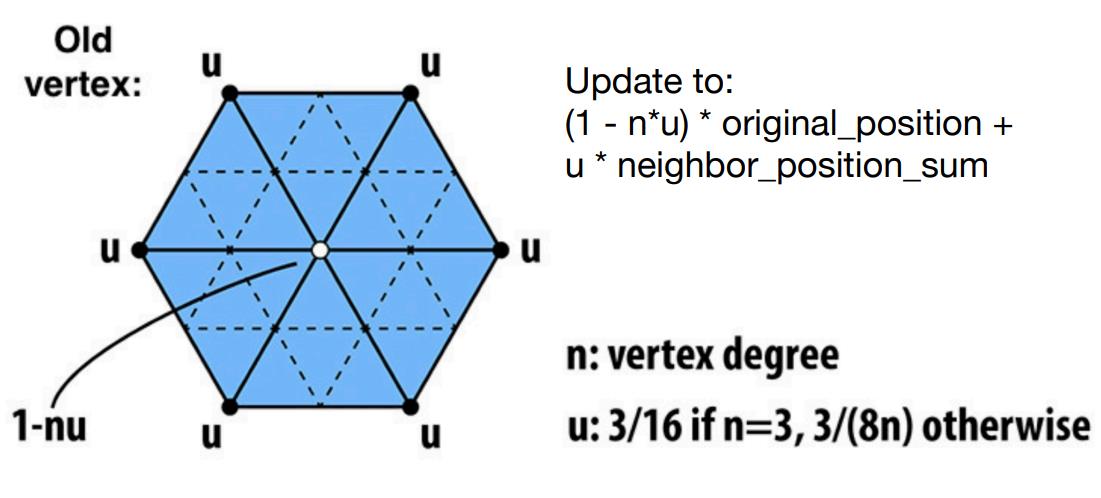
和新顶点一样也是根据权重求,但还需额外考虑n——度数(degree)和u——与n有关的数,公式如下图
Catmull-Clark细分
Loop细分只适用于三角形面,那么对于非三角形面又怎么办呢?这里就需要涉及到Catmull-Clark细分,该算法可以处理多边形的细分
首先,我们说明几个定义:
- Non-quad face:非四边形面
- Extraordinary vertex(奇异点):degree不为4的顶点
对于每次细分,步骤如下:
- 在每条边上取一个新的中点
- 在根据权重在面中取一个新的顶点
- 连接这些新的点
第一次细分
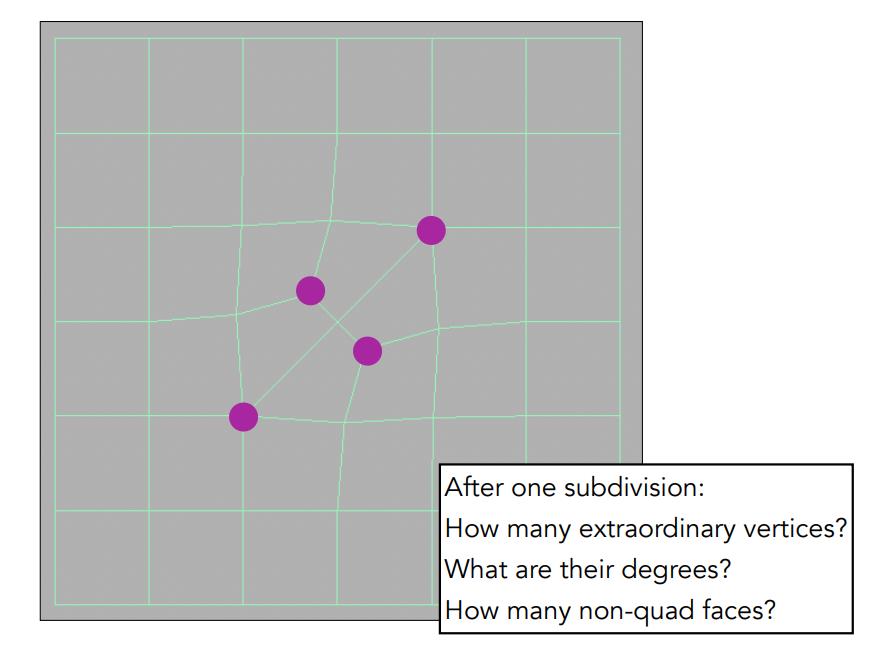
再细分两次
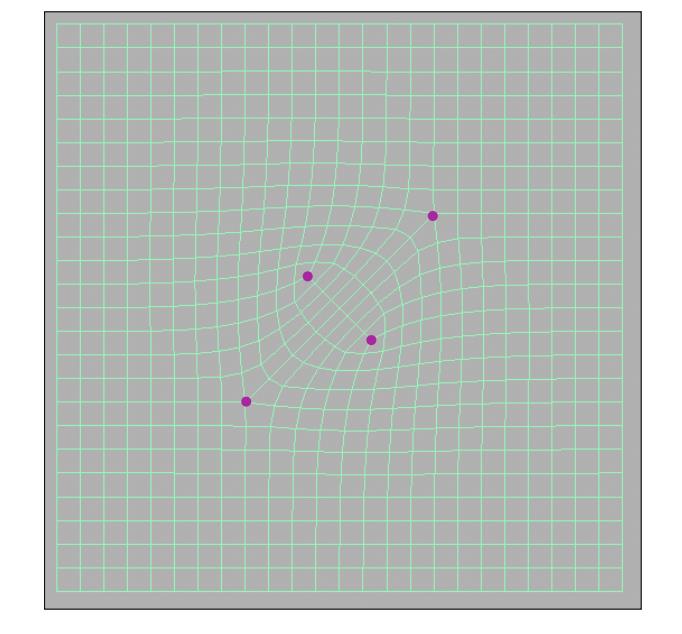
Catmull-Clark细分的特点:
- 所有的面都变为四边形面
- 引入两个degree为3的Extraordinary vertex——每减少一个四边形面会增加一个Extraordinary vertex
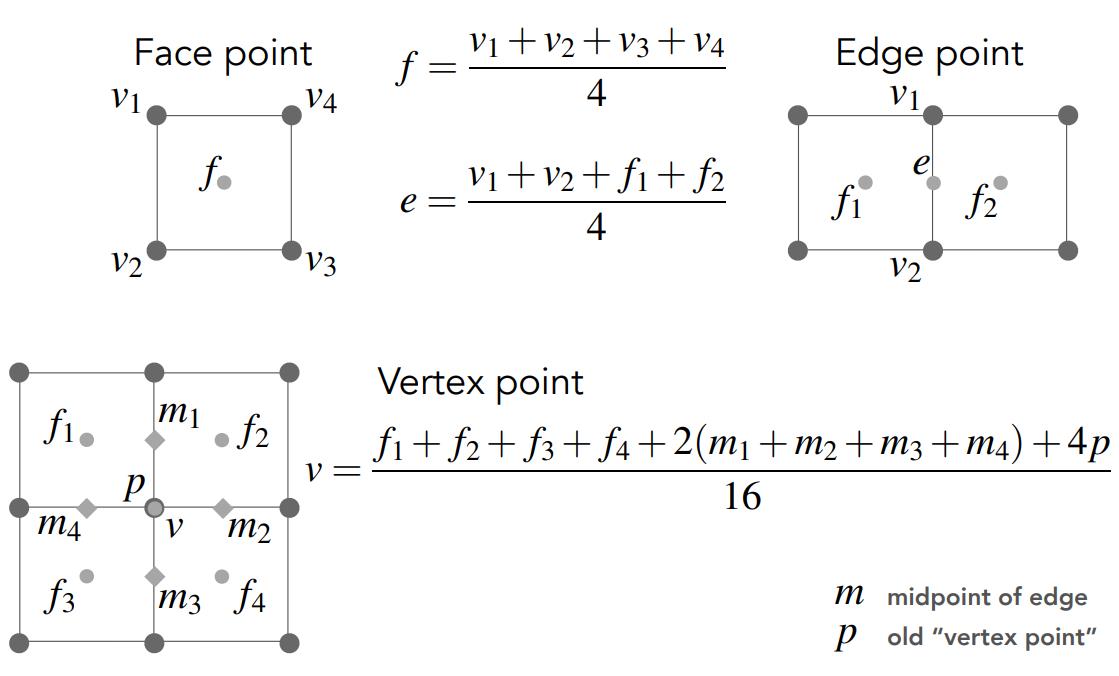
调整顶点位置,对于Catmull-Clark细分将顶点分为三类,它们的调整公式如下:
两种细分的效果
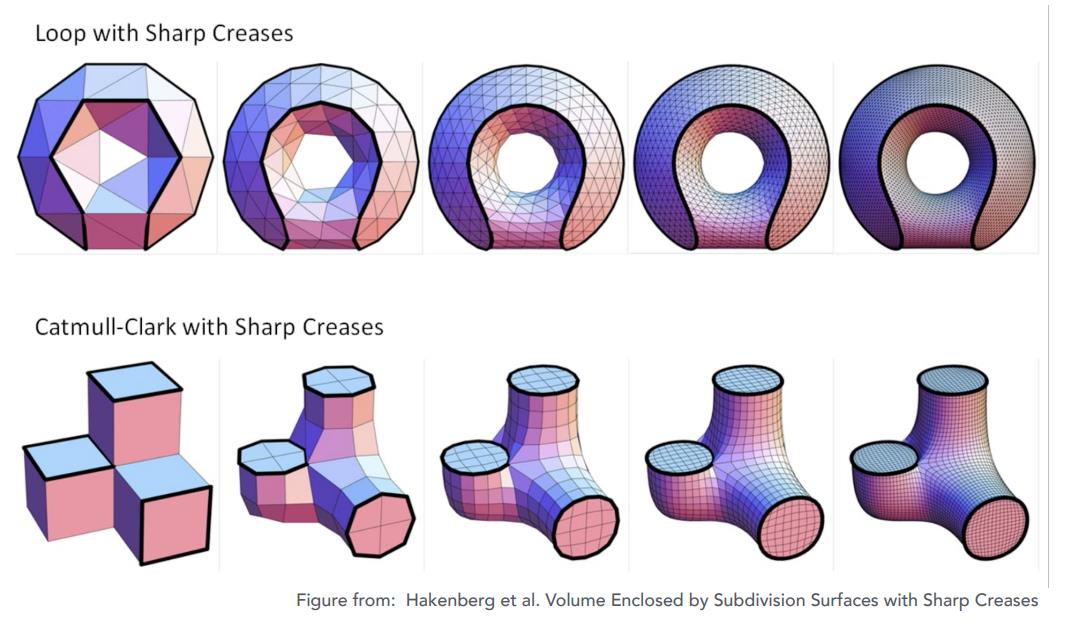
曲面细分的步骤
若启用曲面细分,以下涉及的阶段的处理都将有所不同
Input assembler
在IA阶段,不再向其提交三角形面,而是提交若干含有控制点的面片(patch)。通过控制这些控制点,我们可以对两点之间的线段进行变形,也就是说我们可以将三角形看作是含有三个控制点的三角形面片,且依然可以提交三角形网格,用于网格细分,四边形亦是如此(划分为三角形)
vertex shader
vertex shader不再处理顶点,而是处理的控制点。因为这一点的变化,在曲面细分阶段前,我们可以进行一些动画和物理的计算(细分后,计算量将更大)
hull shader
hull shader(外壳着色器)由常量(constant)外壳着色器和控制点(control point)外壳着色器组成。这两个着色器相当于准备阶段,它们输出必要的值给下一阶段,在下一阶段tessellator stage才会真正执行曲面细分操作
常量外壳着色器
常量外壳着色器的输入是vertex shader的输出,输出是网格的曲面细分因子,该因子表示在曲面细分中将面片细分的段数
我们结合一个实例来看,因为这玩意儿比较抽象
struct PatchTess
float EdgeTess[4] : SV_TessFactor; //面片边缘细分后的段数
float InsideTess[2] : SV_InsideTessFactor; //面片内部细分后横向和纵向被分为多少段
;
PatchTess ConstantHS(InputPatch<VertexOut, 4> patch, uint patchID : SV_PrimitiveID)
PatchTess pt; //细分因子
pt.EdgeTess[0] = 3; //左边缘
pt.EdgeTess[1] = 3; //上边缘
pt.EdgeTess[2] = 3; //右边缘
pt.EdgeTess[3] = 3; //下边缘
pt.InsideTess[0] = 3;
pt.InsideTess[1] = 3;
对于以上实例,我们重点关注两个变量:EdgeTess和InsideTess,假定该面片为四边形面片,SV_TessFactor和SV_InsideTessFactor是系统值,分别表示面片的边缘和内部的细分段数
下图展示不同的EdgeTess和InsideTess所对应的情况
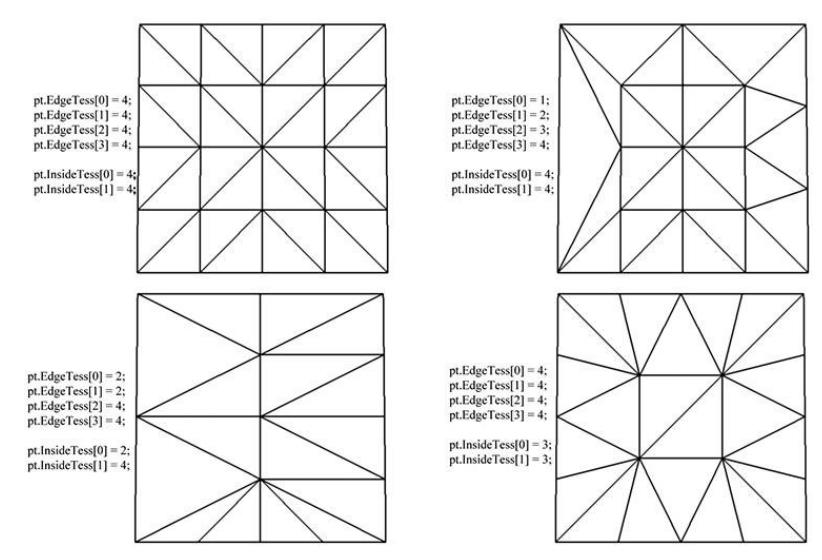
其次,InputPatch<VertexOut, 4> patch中的4指定该面片含有多少控制点,VertexOut表示vertex shader的输出控制点,并且以SV_PrimitiveID提供面片的ID值,该值指定唯一的面片
对于三角形来说,SV_TessFactor和SV_InsideTessFactor分别表示三条边上细分后的段数,内部的细分点数
比如下图中,三角形内部指定四个点——内部一个三角形有三个控制点,而该三角形又包含一个,随后再逐层将这些点和边缘的点相连
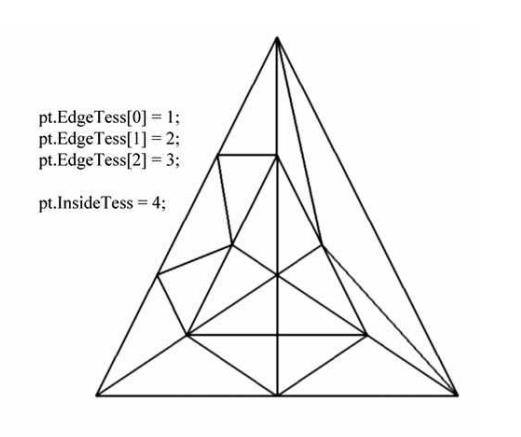
控制点外壳着色器
控制点外壳着色器以多个控制点作为输入,以多个控制点作为输出,该着色器其中一个常用用途是改变曲面的表示方式。比如把一个含有三个控制点的三角形面片转换为三次贝塞尔三角形(含有10个控制点),它的好处是可以丰富视觉效果,且实现方便,无需让美术人员更改模型
还是先来看一个例子:
struct HullOut
float3 PosL : POSITION;
;
[domain("quad")]
[partitioning("integer")]
[outputtopology("triangle_cw")]
[outputcontrolpoints(4)]
[patchconstantfunc("ConstantHS")]
[maxtessfactor(64.0f)]
HullOut HS(InputPatch<VertexOut, 4> p,
uint i : SV_OutputControlPointID,
uint patchId : SV_PrimitiveID)
HullOut hout;
hout.PosL = p[i].PosL;
return hout;
其中,控制点外壳着色器使用以下属性:
SV_OutputControlPointID:指出由控制点外壳着色器正在处理的控制点的索引domain:面片的类型.可选参数有tri(三角形)、quad(四边形)、isoline(等值线)partitioning:曲面细分的细分模式- integer.新顶点的添加/移除取决于
曲面细分因子的整数部分而忽略小数部分,这样会发生明显的popping(假设目标物体本来是棱角分明的石头,随着物体和相机的距离拉近,石头可能会变成球体)。也就是说,该模式模型丰富效果更明显 - 非整型曲面细分.新顶点的添加/移除同样取决于曲面细分因子的整数部分,但细微的"过渡"则取决于曲面细分因子的小数部分.该模式用于把网格平滑过渡到更具细节的网格
- integer.新顶点的添加/移除取决于
outputtopology:细分所创新的三角形的绕序- triangle_cw:顺时针方向
- triangle_ccw:逆时针方向
- line:针对线段曲面细分
outputcontrolpoints:控制点HS执行的次数.每执行一次输出一个控制点patchconstantfunc:常量HS函数名称的字符串maxtessfactor:告知驱动该app所用曲面细分因子的最大值.D3D11支持的最大值为64
tessellator stage
该阶段基于常量HS输出的曲面细分因子对patch进行曲面细分,该阶段会输出新生成的顶点和三角形.该阶段全权由硬件处理,开发人员不能涉及
实例如下:
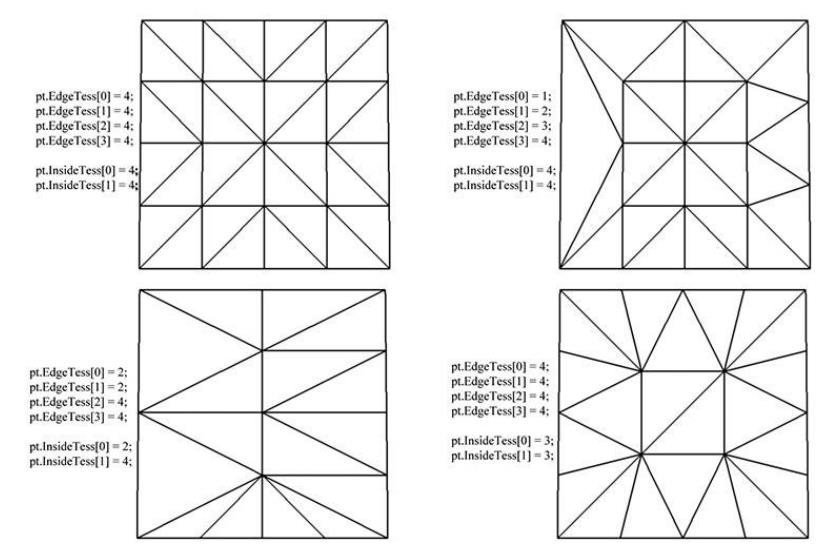
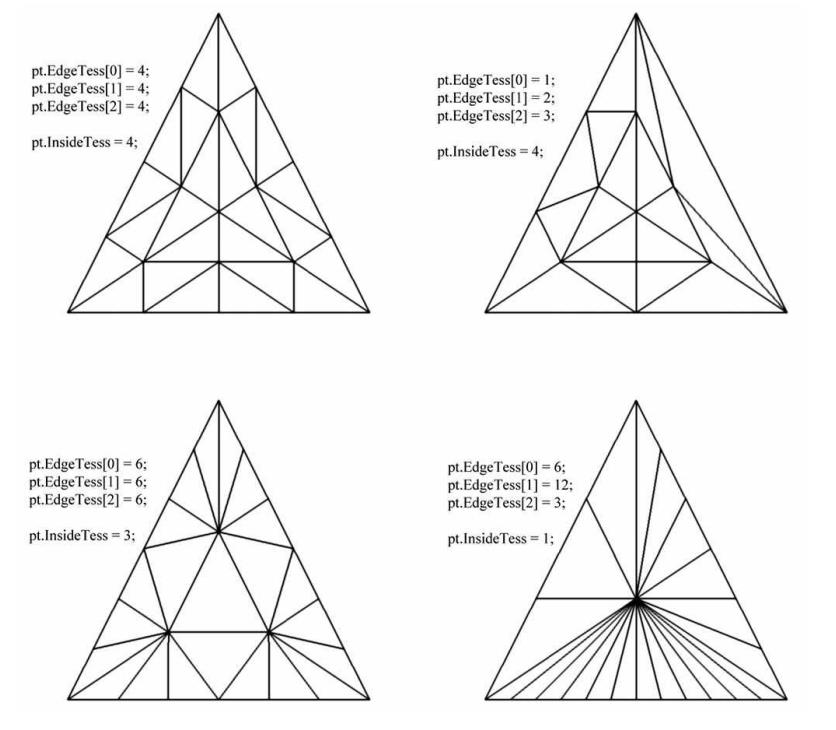
domain shader
tessellator stage输出新生成的顶点和三角形后,domain shader会把这些顶点和三角形作为输入,将它们变换到透视投影空间(因为目前的顶点和三角形处于patch domain 空间),这就相当于原来的vertex shader
domain shader以曲面细分因子、细分后的顶点坐标(u,v)——该uv表示权重 、控制点HS输出的所有面片控制点作为输入,输出为变换到透视投影空间的顶点坐标(但并不是必须要输出该变换后的坐标,这取决于用户自己)。计算四边形的其他顶点只需进行双线性插值,而三角形则进行重心坐标插值
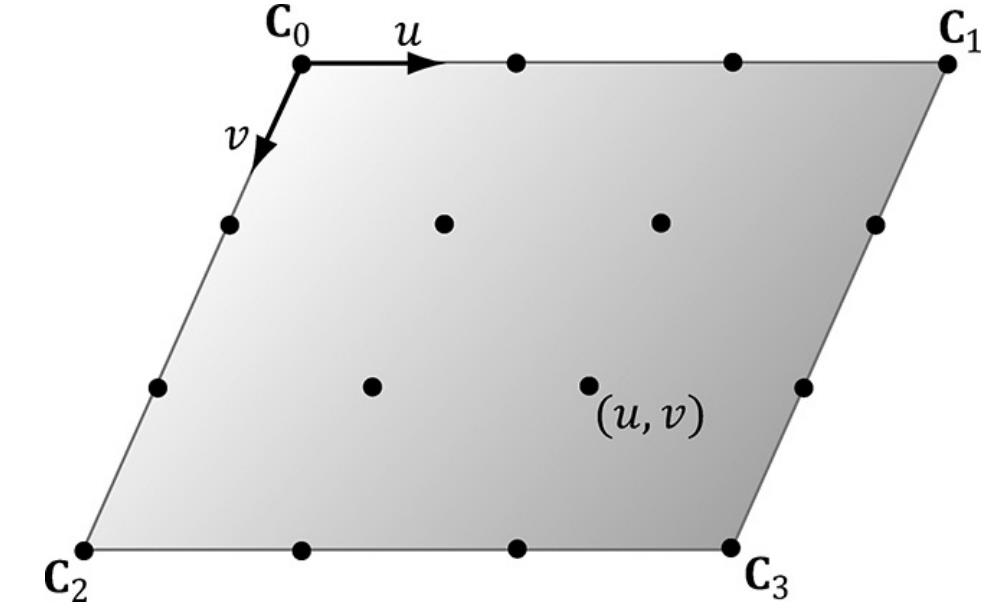
实现:
[domain("quad")]
DomainOut DS(PatchTess patchTess,
float2 uv : SV_DomainLocation,
const OutputPatch<HullOut, 4> quad)
DomainOut dout;
// Bilinear interpolation.
float3 v1 = lerp(quad[0].PosL, quad[1].PosL, uv.x);
float3 v2 = lerp(quad[2].PosL, quad[3].PosL, uv.x);
float3 p = lerp(v1, v2, uv.y);
// Displacement mapping
p.y = 0.3f*( p.z*sin(p.x) + p.x*cos(p.z) );
float4 posW = mul(float4(p, 1.0f), gWorld);
dout.PosH = mul(posW, gViewProj);
return dout;
贝塞尔曲线
什么是贝塞尔曲线?
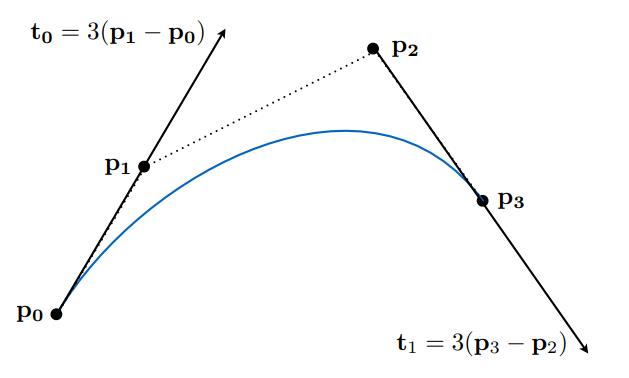
如上图所示,蓝色的曲线便是贝塞尔曲线,其中它由四个控制点\\(p_0, p_1, p_2, p_3\\)绘制而成,它的起点是\\(p_0\\),终点是$p_3。也就是说,贝塞尔曲线是由多个控制点生成的某个曲线
为什么需要贝塞尔曲线?
贝塞尔曲线可以极大提升绘制物体的美感和艺术感。众所周知,在电脑上绘图是十分困难的,尤其是想要绘制出优美的曲线,因此贝塞尔曲线油然而生,它现在是图形中运用的最多的线条之一,是艺术家的梦中情人
绘制贝塞尔曲线
声明一下,含有n+1个控制点的称为n次贝塞尔曲线
2次贝塞尔曲线
de Casteljau算法用于生成2次贝塞尔曲线,步骤如下:
- 定义三个点
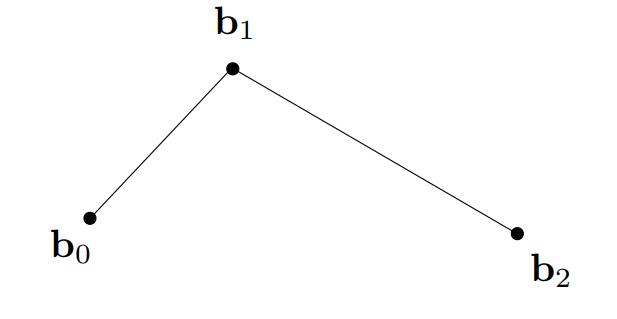
- 在\\(b_0\\)、\\(b_1\\)和\\(b_1、b_2\\)间以任意的t值进行插值生成新的顶点
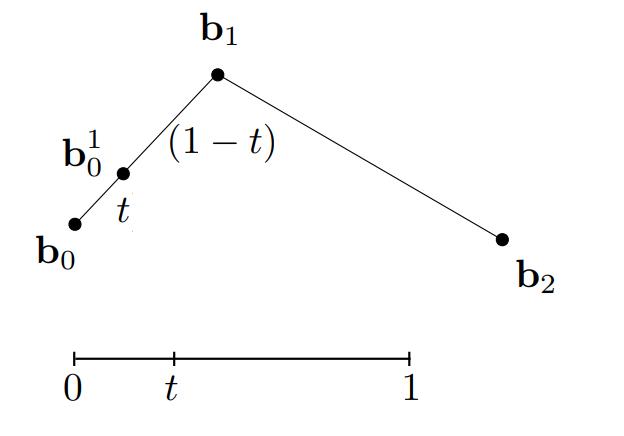
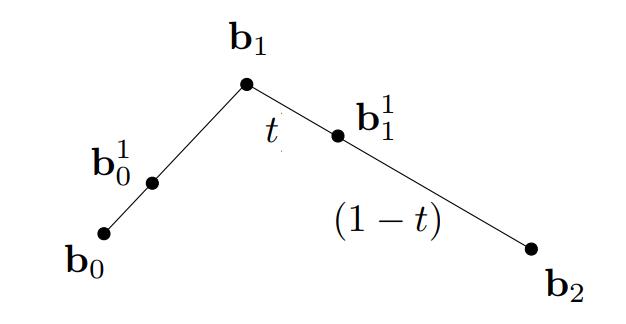
- 连接新生成的顶点,继续插值
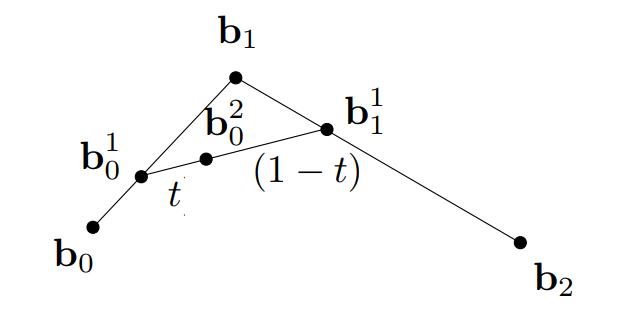
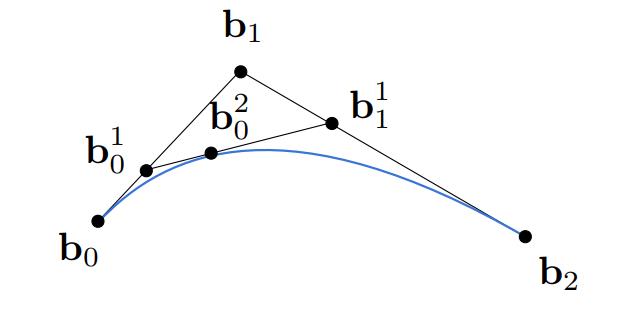
- 基于插值生成的点即可绘制2d贝塞尔曲线
3次贝塞尔曲线
依旧是用de Casteljau算法生成3d贝塞尔曲线,步骤和2次的类似
生成的实例如下:
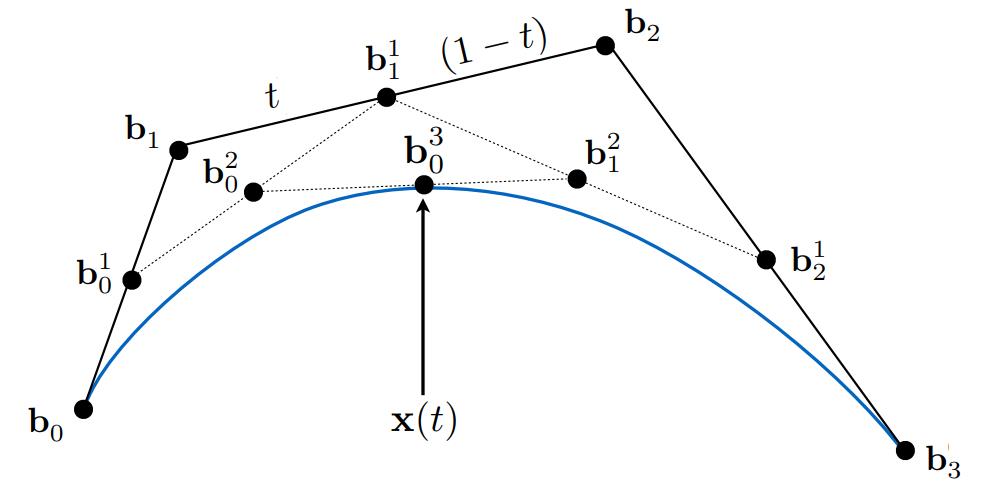
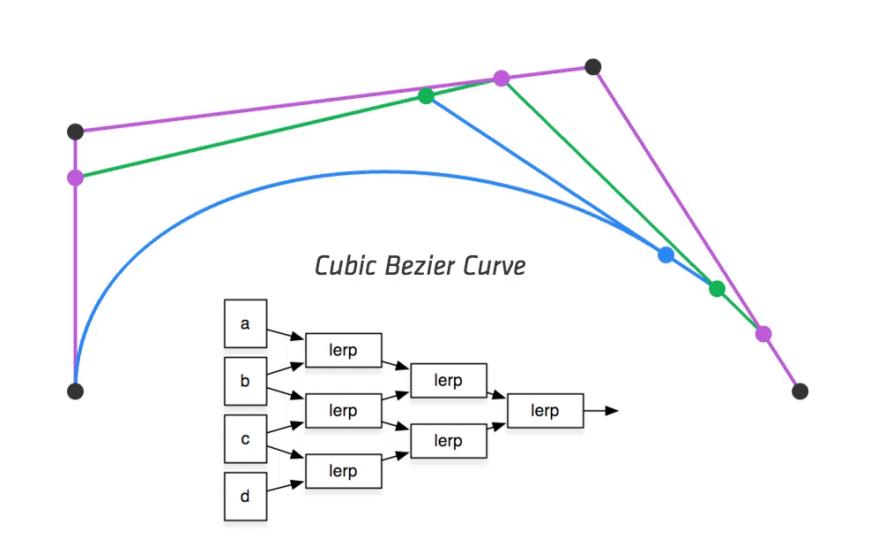
代数表示
总结一下上述三次贝塞尔曲线,每两个点之间进行线性插值
-
状态图如下:
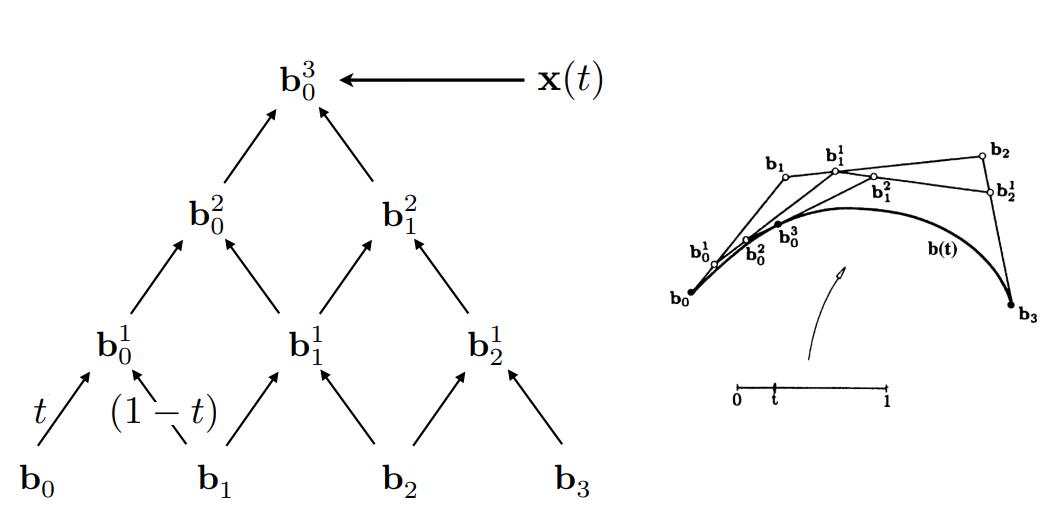
-
转换为代数形式如下:
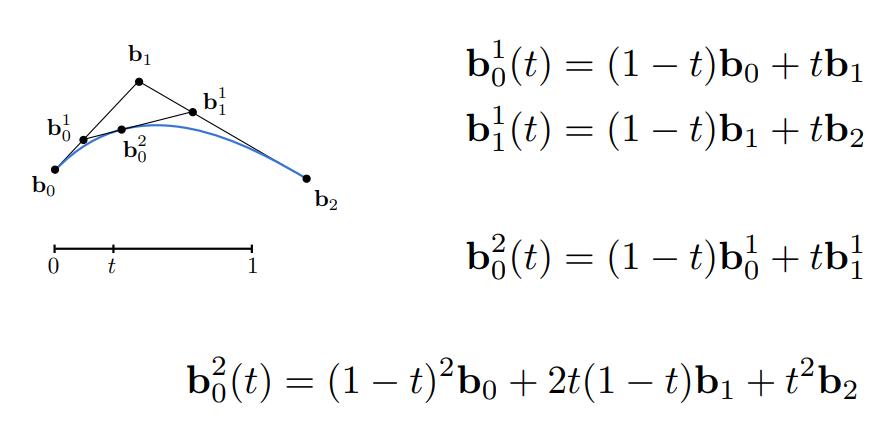
-
再将其推广至n次,可以看出这是一个二项分布的多项式.
-

这里的\\(\\left( \\begin array cc n \\\\ i \\end array \\right)\\)意为组合数,也就是\\(\\large \\fracn!i!(n-i)!\\)
-
比如三次的如下:
-

性质
- 经过起始与终止控制点
- 经由起始与终止线段相切
- 带有仿射变换性质,可以通过移动控制点移动整条曲线
- 凸包性质:曲线不会超出所有控制点构成的多边形范围
reference
https://games-cn.org/intro-graphics/
DirectX12 3D
以上是关于曲面细分阶段的主要内容,如果未能解决你的问题,请参考以下文章