[概率论与数理统计]笔记：5.3 置信区间
Posted feixianxing
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[概率论与数理统计]笔记：5.3 置信区间相关的知识，希望对你有一定的参考价值。
记录置信区间的相关概念，以及关于正态总体参数的置信区间的公式总结。
5.3 置信区间
前言
点估计无法提供其估计的误差，而区间估计可以。
案例：“某人的月薪比2k多，比20k少”，这就是一个区间估计。
区间估计的好坏有两个衡量指标：
- 区间长度
- 真实值落在该区间的概率
我们希望区间长度足够小，而真实值落在该区间的概率又足够大。
事实上，这两个指标是矛盾的，如果概率很大，会导致区间变大；如果区间长度变小，落在区间内的概率就会变小。
定义
- \\(\\theta\\)是要估计的参数。
- \\((\\underline\\theta,\\overline\\theta)\\)是置信区间，其中\\(\\underline\\theta\\)是置信下限，\\(\\overline\\theta\\)是置信上限。
- \\(1-\\alpha\\)是置信水平，或者叫置信度。
做题的时候一般是题目告知置信度，然后需要求解置信上下限。
表述
\\((\\underline\\theta,\\overline\\theta)\\)能套住\\(\\theta\\)的概率是\\(1-\\alpha\\)。
这里需要区分两种表述：
- \\((\\underline\\theta,\\overline\\theta)\\)能套住\\(\\theta\\)的概率是\\(1-\\alpha\\)。
- \\(\\theta\\) 落在 \\((\\underline\\theta,\\overline\\theta)\\)的概率是\\(1-\\alpha\\)。
需要明确的是，\\(\\theta\\)虽然是未知的，但是是确定的。\\(\\theta\\)准确地固定在数轴上的一个位置，只是我们不知道在哪里。我们使用区间\\((\\underline\\theta,\\overline\\theta)\\)来做多次试验，每次试验的区间是随机的不同的，因此\\(\\theta\\)有时会被区间套住，有时候不会。
因此，我们使用的表述是套住，而不是落在。后者是针对不确定的值时候的表述。
枢轴变量
定义
为了求解置信区间，需要构造枢轴变量
其中\\(\\theta\\)是未知参数，\\(T\\)是已知的，\\(I\\) 的分布已知且与\\(\\theta\\)无关。
对于给定的\\(1-\\alpha\\)，确定\\(F\\)的上\\(\\frac\\alpha2\\)分位数，记为\\(u_\\frac\\alpha2\\)；确定\\(F\\)的上\\((1-\\frac\\alpha2)\\)分位数，记为\\(u_1-\\frac\\alpha2\\)，那么就会有
图解
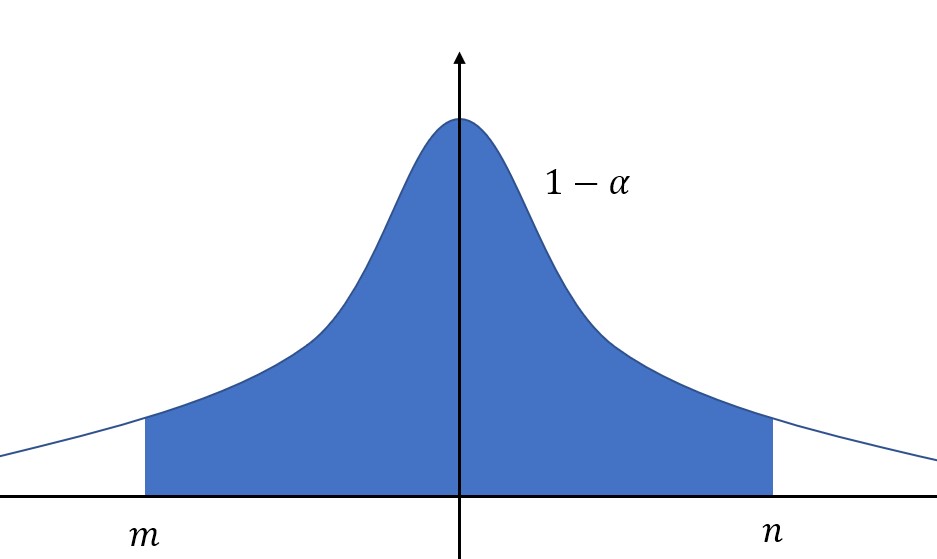
对于给定的置信度，也就是概率\\(1-\\alpha\\)，我们的目的是求解区间上下限，也就是图中的\\(m\\)和\\(n\\)。
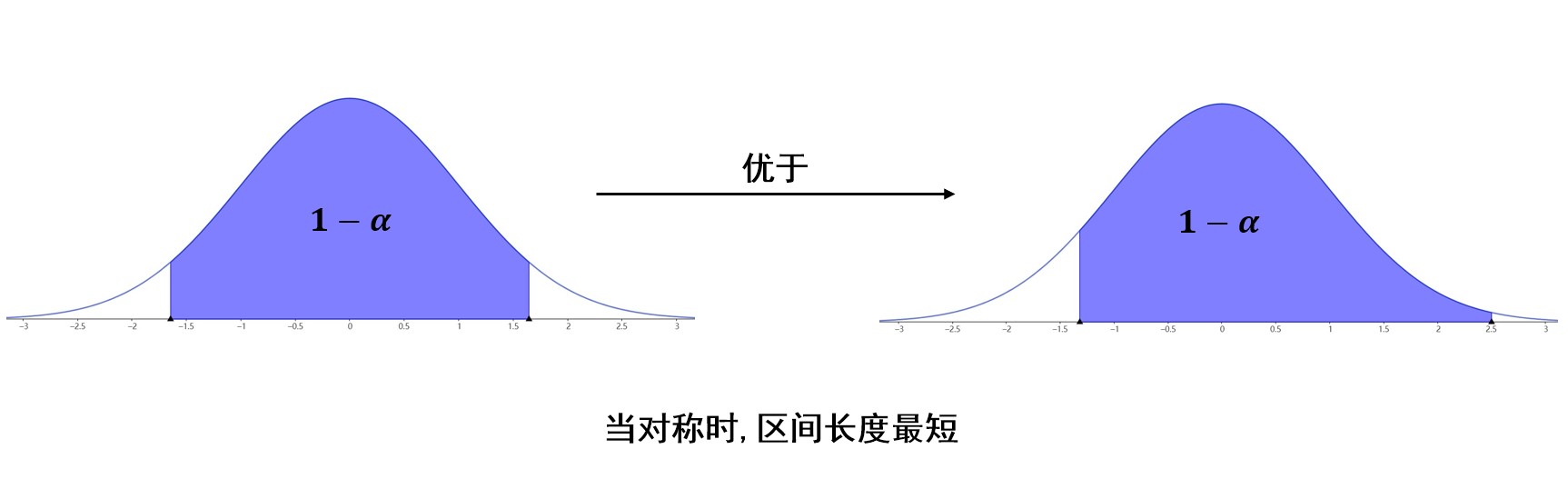
值得注意的是，我们希望区间长度小一些，如果研究的分布是正态分布，或者密度函数类似于上图，那么在置信度一定的情况下，即图中蓝色区域面积一定，只要选定区间位于中间，关于\\(y\\)轴对称，那么区间长度就是最小的。（因为峰值在中间）
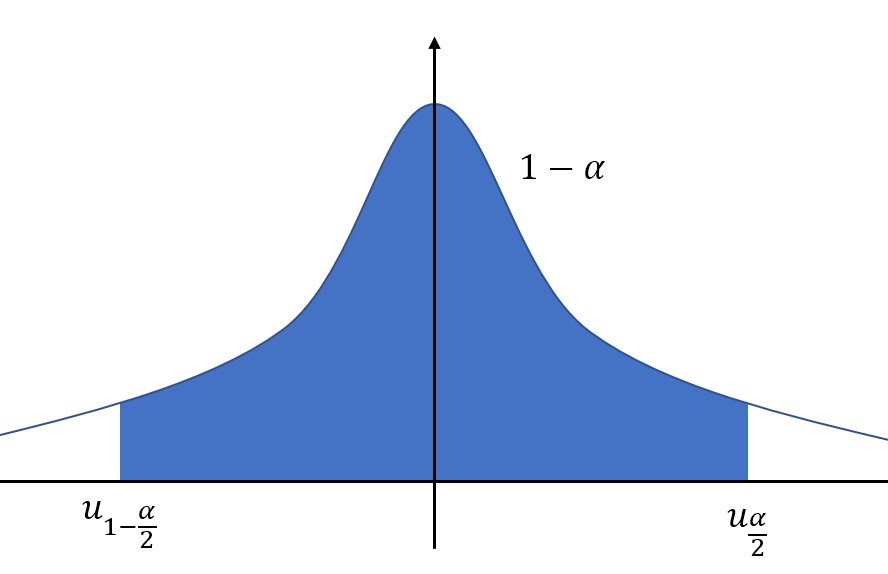
当置信区间位于中间时，置信度为\\(1-\\alpha\\)，那么左右两个置信上下限就可以通过上侧分位数表示了。
中间的阴影面积为\\(1-\\alpha\\)，那么左右两侧的空白面积就分别是\\(\\frac\\alpha2\\)。
置信上限使用上侧分位数表示就是：\\(u_\\frac\\alpha2\\).
置信下限使用上侧分位数表示就是：\\(u_1-\\frac\\alpha2\\).
总结
构造枢轴变量的目的是为了求解置信区间，将枢轴变量构造成我们熟悉的分布，比如正态分布，\\(t\\)分布，\\(F\\)分布。然后就可以利用这些分布的性质列出不等式，然后求解出我们要估计的参数的区间。
需要注意的是，枢轴变量只能包含一个未知的参数，即我们要估计的参数\\(\\theta\\)，只有这样才能进行不等式化简。
正态总体参数的置信区间
均值\\(\\mu\\)的置信区间
情况1：方差\\(\\sigma^2\\)已知
总体方差\\(\\sigma^2\\)已知，估计\\(\\mu\\)，此时\\(\\mu\\)是未知参数。
构造枢轴量：
相关知识点：
以上是关于[概率论与数理统计]笔记：5.3 置信区间的主要内容，如果未能解决你的问题，请参考以下文章