torch.optim.SGD参数详解

Posted 2022-03-31 Blair

 

随机梯度下降法

　　　　$\\theta_t \\leftarrow \\theta_t-1-\\alpha g_t$

Code：

optimzer = torch.optim.SGD(model.parameters(),lr = 0.001)

权重衰减

　　　　$\\theta_t \\leftarrow(1-\\beta) \\theta_t-1-\\alpha \\mathbfg_t$
　　其中 $\\mathrmg_t$ 为第 $t$ 步更新时的梯度, $\\alpha$ 为学习率, $\\beta$ 为权重衰减系数，一般取值比较 小，比如 0.0005。

　　

Code：

optimzer = torch.optim.SGD(model.parameters(),lr = 0.001,weight_decay=0.0005)

动量法 

　　动量（Momentum）是模拟物理中的概念．一个物体的动量指的是该物体 在它运动方向上保持运动的趋势，是该物体的质量和速度的乘积．动量法（Momentum Method）是用之前积累动量来替代真正的梯度．每次迭代的梯度可以 看作加速度． 在第 $t$ 次迭代时，计算负梯度的“加权移动平均”作为参数的更新方向，

　　　　$\\Delta \\theta_t=\\rho \\Delta \\theta_t-1-\\alpha g_t=-\\alpha \\sum\\limits_\\tau=1^t \\rho^t-\\tau g_\\tau$

　　

Code：

optimzer = torch.optim.SGD(model.parameters(),lr = 0.001,momentum =0.001,dampening=0.001)

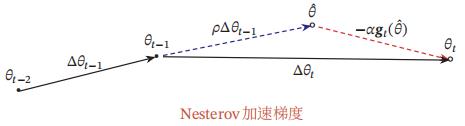
Nesterov加速梯度

　　 Nesterov 加速梯度（Nesterov Accelerated Gradient，NAG）是一种对动量 法的改进[Nesterov, 2013; Sutskever et al., 2013]，也称为Nesterov动量法（Nesterov Momentum）

　　在动量法中, 实际的参数更新方向  $\\Delta \\theta_t$  为上一步的参数更新方向  $\\Delta \\theta_t-1$  和当 前梯度的反方向 $ -g_t$  的叠加. 这样,  $\\Delta \\theta_t$  可以被拆分为两步进行, 先根据  $\\Delta \\theta_t-1$  更 新一次得到参数 $ \\hat\\theta$ , 再用 $ -g_t$  进行更新.

　　这样，合并后的更新方向为

　　　　$\\Delta \\theta_t=\\rho \\Delta \\theta_t-1-\\alpha \\mathfrakg_t\\left(\\theta_t-1+\\rho \\Delta \\theta_t-1\\right)$

　　其中 $\\mathfrakg_t\\left(\\theta_t-1+\\rho \\Delta \\theta_t-1\\right)$  表示损失函数在点 $\\hat\\theta=\\theta_t-1+\\rho \\Delta \\theta_t-1$ 上的偏导数. 

　　

　　

Code：

optimzer = torch.optim.SGD(model.parameters(),lr = 0.001,momentum =0.001,nesterov=0.01)

 

因上求缘，果上努力~~~~ 作者：Learner-，转载请注明原文链接：https://www.cnblogs.com/BlairGrowing/p/16079975.html