关于树（图论初步）

Posted 2022-03-25 你的小垃圾

今天学了关于树的最最最最基本的有关概念和性质，做一下简单的记录：

首先，树是什么？？？

其实简单点来说，树就相当于一个元素之间有确定关系的集合。其中每个元素都是一个结点，他们两两以特定的方式连接并相互关联，而树就是由递归定义与实现的。例如，下图就是一个典型的树：

 

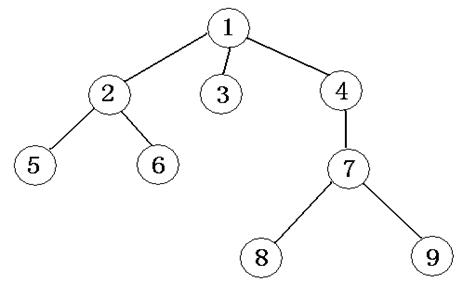
其中，元素1~9都是结点，而1上面没有结点与它连接，所以它就是一个特殊的结点——树根。

除了根结点，其他的结点能分成很多个互不相交的有限集合，而其中的几个互相连接的结点元素就可以组成一棵子树。

每一个结点的子树的个数，叫做这个结点的度，其实这个结点连接的有几个子结点它的度就是几，比如图中的4，他就有1个子节点，所以它的度就是1，而3下面没有跟它连接的子结点，所以它的度就是0。

特别的，如果这个结点的度是0，那这个结点就叫做叶节点，如图中的5,6,3,8,9就都是叶结点。

上面的结点是下面结点的父节点，下面的是上面的子结点，有相同父节点的子结点互为兄弟结点。

下面来道水题练练手：

要求先输入两个数 n、m，表示一棵树的结点数和边数，再输入m行，每行输入一个父节点 x 和一个x的子结点 y。现在要求输出树根，子结点最多的结点 和 此节点的子结点。（数据范围忽略）

思路其实就是桶的思想，先输入每个x和y，并记录y的父节点x。全部输入完之后再判断，如果没有父节点，那这个点就是树根。最后再用一个循环嵌套遍及每一个结点，记录他子结点的个数，找出最大值就好了。

代码如下：

 #include<iostream>
 using namespace std;
 int n,m;
 int tree[100]=0;//记录父节点 
 int ans,sum,maxn;
 int main()
 
     int x,y;
     scanf("%d%d",&n,&m);
     for(int i=1;i<=m;i++)
         scanf("%d%d",&x,&y);
         tree[y]=x;
     
     for(int i=1;i<=m;i++)
         if(tree[i]==0)
             printf("%d\\n",i);
             break;
         
     
     for(int i=1;i<=n;i++)
         sum=0;
         for(int j=1;j<=n;j++)
             if(tree[j]==i) sum++;
             if(sum>maxn)
                 maxn=sum;
                 ans=i;
             
         
     
     printf("%d\\n",ans);
     for(int i=1;i<=n;i++)
         if(tree[i]==ans)
             printf("%d ",i);
         
     
     return 0;
 

 

关于树的遍历，有好几种：

1、先序遍历：先访问根结点，再从左往右的访问每一棵子树，与DFS相似，在上图中遍历顺序就是125634789

2、后续遍历：先从左到右先遍历每一棵子树，最后访问根结点，在上图中遍历的顺序就是562389741

3、层次遍历：一层一层地遍历，在图上遍历的顺序就是123456789

4、叶结点遍历：上图按照这个思想访问的结果为：56389；

5、中序遍历：左儿子——父节点——右儿子（前提是必须是二叉树）。

 

关于二叉树：

二叉树是一种特殊的树形结构，除了叶节点，其余的每个节点的度都小于等于2，也就是说每个父节点都最多有两个子结点。下图是二叉树的五种形态：

 

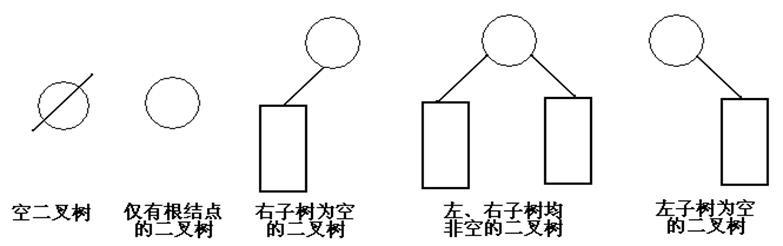
关于二叉树的性质：

1、在二叉树的第i层上最多有 2 的 i-1 次方个结点

证明：二叉树的第一层至多有2的零次方个结点，第2层至多有2的一次方个结点，因为每个节点最多有两个儿子，所以每一层都是上一层的结点数乘2，那第 i 层自然就是2^（i-1）个结点。

2、层数（深度）为k的二叉树最多有 2^k  -1个结点

证明：由于第1层有2^0个结点，第2层有2^1个结点，那第k层至多有2^（k-1）个结点，

则总结点数就是：2^0+2^1+……+2^（k-1）=2^0+2^0+2^1+……+2^（k-1）-2^0=2^1+2^1+2^2+……+2^（k-1）-1=2^k  -1

3、如果一棵二叉树叶结点数为n0，度为2的结点数为n2，则一定满足：n0=n2+1

证明：对于父节点一定对应两子结点的子树，设一共x层，那非子结点的个数就是前x-1层的个数，由性质2得出前x-1层的个数为2^（x-1）-1，由性质1得出第x层上的子结点个数为2^（x-1）个，所以两者相差1。

4、有n个结点的完全二叉树（最下层的叶节点左边是满的，右边可以为空，如下图）的深度为：floor（log2 n）+1

证明：设结点数是n，深度是k，由性质2得：n=2^（k-1）为指数函数，转换成对数函数就是：log2 n=k-1。即 k=floor（（log2 n）+1），由于人家不一定是满的，要加一个下取整。

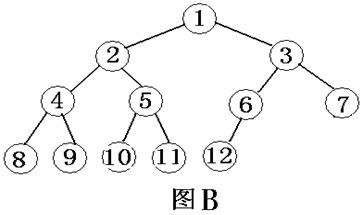（如图就是一棵完全二叉树）

5、对于任意的完全二叉树的某个标号为n的左结点，此结点的父节点的标号为n/2，兄弟结点的标号n+1，左儿子为2n，右儿子为2n+1。

 

那么我们怎么把一棵多叉树转换成一棵二叉树呢？？

对于每一个根结点，把只保留它最左端的子结点与它相连，其他的结点与他的根结点断开，再与其左边的一个兄弟结点相连就好了。如下图：

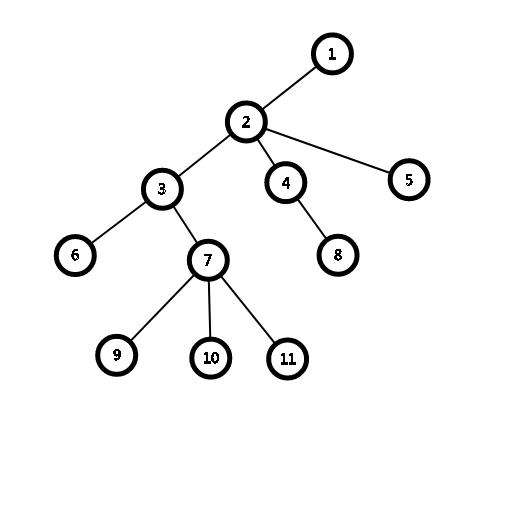
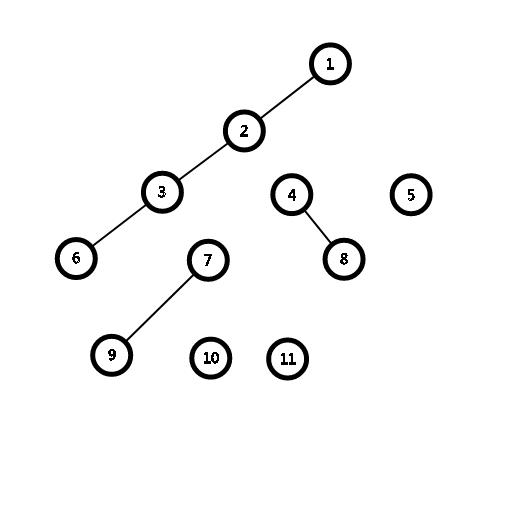
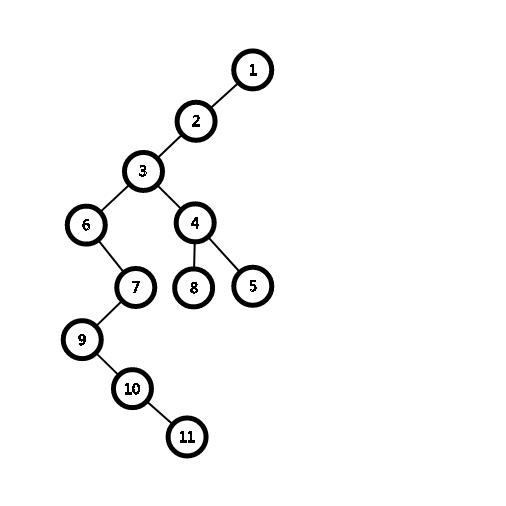
一道简单的练习题：

q：一棵完全二叉树的结点总数是18，其叶节点数是？

a：由性质4得出此二叉树的层数为floor（log2  18）+1=5

由性质2的前4层（由于是完全二叉树，前4层一定是满的）的结点数是2^4 -1=15

所以最后一层有18-15=3个结点，最后一层的三个子结点用掉了上一层的2个父结点

第四层有2^（4-1）=8个子结点，用掉俩还剩6个没有子结点的结点，他们也是叶结点

所以一共有3+6=9个子结点

 

遍历二叉树的代码实现：

1.先序遍历：先访问根结点，再遍历左二叉树，最后遍历右二叉树。

 void preorder(tree bt) //先序递归算法
  
   if(bt)
      cout << bt->data;
      preorder(bt->lchild);
      preorder(bt->rchild);
     
 

2、中序遍历：先遍历左二叉树，再访问根结点，最后遍历右二叉树。

 void inorder(tree bt)  //中序遍历递归算法
 
 　 if(bt)
 　     inorder(bt->lchild);
 　　　cout << bt->data;
 　　　inorder(bt->rchild);
 　   
 

3、后序遍历：先遍历左二叉树，再遍历右二叉树，最后访问根结点。

 void postorder(tree bt)  //后序递归算法
 
       if(bt)
         
           postorder(bt->lchild);
            postorder(bt->rchild);
           cout << bt->data;
     
 

关于一棵表达式树，可以分别用先序，中序，后序遍历方法得到3钟不同的遍历结果：

 

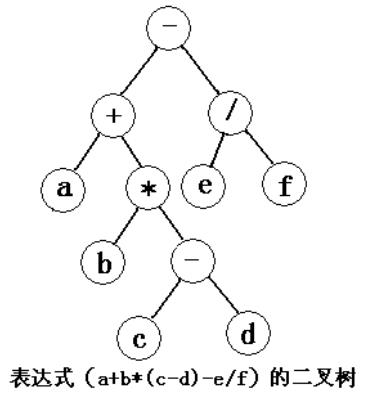
 前缀表示（波兰式）：- + a * b - c d / e f

中缀表示：a + b * ( c - d ) - e / f

后缀表示（逆波兰式）：a b c d - * + e f / - 

还有就是关于二叉树的唯一性：

知道先序或后序其中的一个和中序就可以确定一棵树，但是只知道先序和后序就不可以，比如：

 

 

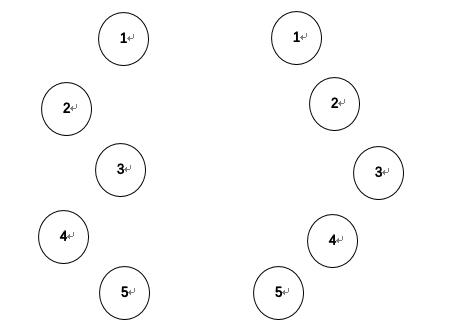
 二叉树基操：

1、建树

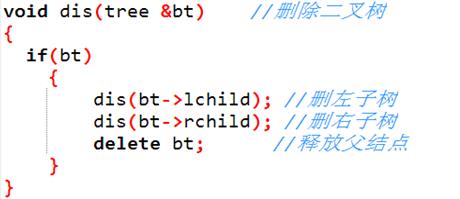
 2、删树

 3、插点

我来模拟一下，假设现在我有一个排好序了的二叉树，排序规则是对于任意一个子树根，他的左子树上的结点都比子树根小，右子树上的结点都比它大。

那我现在就用一个递归，如果输入的数比根结点小那就递归左子树，如果大就递归右子树，直到找到合适的位置就把他加进去

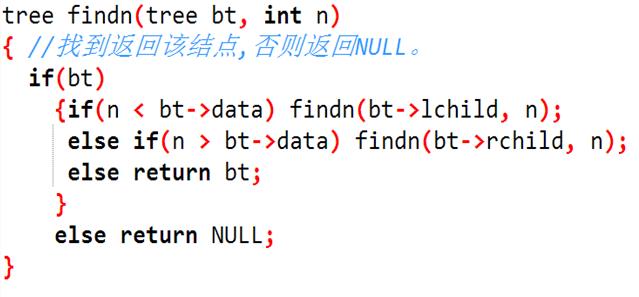
4、查找

其实也跟插点的思想差不多，类似于二分查找，找到就返回该点，找不到就返回NULL

来几道题练练手吧

注意！！下面的操作均用到指针！！！当然，如果你不想用指针的话，那就直接往下滑吧！！！

【问题描述】

由于先序、中序和后序序列中的任一个都不能唯一确定一棵二叉树，所以对二叉树做如下处理，将二叉树的空结点用·补齐，称为原二叉树的扩展二叉树，扩展二叉树的先序和后序序列能唯一确定其二叉树。
现给出扩展二叉树的先序序列，要求输出其中序和后序序列。

【输入样例】
ABD..EF..G..C..

【输出样例】
DBFEGAC
DFGEBCA

题解如下：

【问题描述】
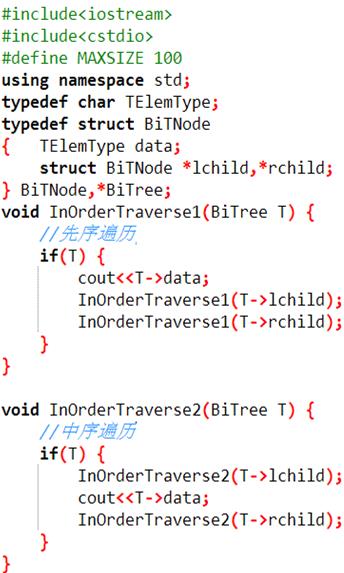
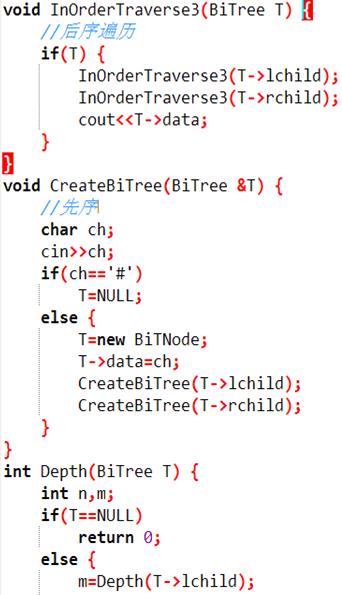
以二叉链表作存储结构，建立一棵二叉树，并输出该二叉树的先序、中序、后序遍历序列、高度和结点总数。

【输入样例】
12##3## //#为空

【输出样例】
123 //先序
213 //中序
231 //后序
2 //高度
3 //结点总数

题解如下：

 ————————————————————————————————————手动分隔线——————————————————————————————————————————

下面是不用指针的：

输入一棵树的前缀和中缀，求后缀：

代码如下：

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #define ll long long
 using namespace std;
 char qian[100005],zhong[100005];
 int q[100005],z[100005],a[100005];
 int cnt=0;
 void find(int start,int end)
 
     if(start>end)
         return;
     
     cnt++;
     if(start==end)
         cout<<char(z[q[cnt]]+\'a\'-1);
         return;
     
 //等于的话说明我现在只有一个字母了，这个字母就是最左的那个字母，我把它输出，然后返回再继续找 
     int t=cnt;
     find(start,q[t]-1);
     find(q[t]+1,end);
     cout<<char(z[q[t]]+\'a\'-1);
 
 int main()
     scanf("%s%s",qian+1,zhong+1);
 //先输入前序和中序 ,从下标1开始 
     int len=strlen(qian+1);
     //这里要加上个1 
     for(int i=1;i<=len;i++)
         a[zhong[i]-\'a\']=i;
     
 //记录每个字母在中序中的位置
 //比如我第一个输入的是c，那么c在中序中的位置就是：
 //a[\'c\'-\'a\']=1,即c对应的在中序排列中的位置是第1个 
     for(int i=1;i<=len;i++)
         z[i]=zhong[i]-\'a\'+1;
 //记录的是一个字母在中序排列中的对应的下标
 //比如还是c，他的下标就是\'c\'-\'a’+1=3 
         q[i]=a[qian[i]-\'a\'];
 //现在遍历前缀表达式的每一个字母，比如现在我在i=2的时候遍历到c，
 //那也就是说q[2](前缀表达式中的第2位的字母c他在中缀表达式中的位置是q[2]）
  //记录q[2]= a[qian[2]-\'a\']，( a[qian[i]-\'a\']就是中序第i个字符在前序的位置 
  
     find(1,strlen(qian+1));
    //从第一位到最后一位开始找 
     return 0;
 

 思路是这样的：

首先记录前缀和中缀，找到前缀在中缀中的位置：

建立一个a数组代表中缀的每个字母在在中缀中的位置，也就是 a[zhong[i]-\'a\']=i，也就是说中缀表达式中的第 i 个位置的字符，他的位置是 i 。

然后建立了一个z数组，代表中缀表达式中的第 i 个位置的字符他对应的数字大小；

再建立一个q数组，代表前缀表达式中的第 i 个字符在中缀表达式中的位置。

然后定义一个查找函数，定义一个前和一个后代表查找的范围，由于后缀是“左——右——头”，我要先找到那个没有儿子的左叶结点和右结点，之后再查找子树的根结点

因为前序是先头再其他，所以从前缀表达式的第一个字符开始，找到他在中缀表达式中的位置，以其为断点将中缀表达式分成两段，左段就是左子树，右段就是右子树，一直找下去，直到前和后一样了，也就说明这个点就是最左端的叶结点，输出它，也就是输出前缀表达式中的这个字符对应的位置在中缀表达式中的值对应的字符，再返回。继续找，找完之后再找右边的，道理跟他一样，在输出右边的字符，最后在输出子树的根节点就好。

 

输入中缀和后缀，求前缀：

思路跟前面那道题很相像，但有一点不同的是，根结点在后缀的最后，所以我们要倒着找，但这就导致了一个问题：如果倒着找，那就成先找右儿子再找左儿子了，要是这样的话要想找到下一个子树的根结点就要跳着找。针对这种问题，我们可以通过区间求找的方式解决，具体解决过程的方法解析我放下面代码里了

代码如下：

 #include<iostream>
 #include<string>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 string zhong,hou;
 void find(int zl,int zr,int hl,int hr); //区间查找，待会再讲 
 int main()
 
     cin>>zhong>>hou;
     find(0,zhong.size(),0,hou.size());//就是找 
     return 0;
  
 void find(int zl,int zr,int hl,int hr) 
 //这四个分别代表：中序左端，中序右端，后序左端，后序右端 
 
     cout<<hou[hr-1];//后序的最后一个肯定是（当前子树的）根结点，那就先输出它！ 
     int p=zhong.find(hou[hr-1]);
 //和上一题的思路一样，就是找到后序的最后一个（也就是子树的根结点）在中序中的位置。 
     if(p>zl) find(zl,p,hl,hl+p-zl);
 //要分段了，在左边我们要找的是从左端到根结点
 //关键就是下一个根结点就不是后序中的下一个了
 //所以我们要找到跳一段后的后序区间。
 //我们知道的是左端是hl，因为这两段的长度是一样的（你可以枚举画图并试图自己理解一下），所以可以列出等式：
 // p-zl=x(我设的后序右端位置）-hl,解得：x=hl+p-zl 
     if(p+1<zr) find(p+1,zr,hr+p-zr,hr-1);
 //这个也一样，也是两个区间的长度相同，我就不再推了 
 

 

还有就是以先序顺序输入一棵二叉树，让输出先序、中序、后序排列、层数和总结点数

思路我在下面写的很明白了（吧？），这里就不说了，直接看吧

 #include<iostream>
 #include<cstdio>
 #define ll long long
 using namespace std;
 int num,maxn;//代表结点总数、高度 
 char s;
 
 struct t
     int data,father,lson=0,rson=0,h=0;
 tree[100005];
 //data代表当前结点的数值，father代表他爹的下标 
 
 void build(int father,bool right)
 //这个函数主要是为了找出最高高度(maxn)和总结点数(num) 
 //father记录下标，right判断是他爹的左儿子还是右儿子 
 //如果right是0就是左儿子，1就是右儿子 
 
     cin>>s;
     if(s==\'\\n\')
     return;
     if(s!=\'#\')
         ++num;
 //num记录到了第几个下标，也是目前一共读入了多少个 
         int t=num;
         tree[t].father=father;
 //当前位置的结点的爸爸就是他的爸爸 
         tree[t].data=s-\'0\';
         tree[t].h=tree[father].h+1;
         maxn=max(tree[t].h,maxn);
         if(right==0)//如果是左儿子 
         tree[father].lson=t;//他爸爸的左儿子就是它 
         else
         tree[father].rson=t;//他爸爸的右儿子就是它 
         
         build(t,0);//他要当爹，找他左儿子 
         build(t,1);//让它当爹，找右儿子 
     
     else return;
 
  
 void xian(int now)
 //这个now代表的是当前状态 
 
     cout<<tree[now].data;
 //由于是先序，就先输出爸爸 
     if(tree[now].lson!=0)
         xian(tree[now].lson);
     
 //为啥要判断左儿子是不是等于0呢？
 //因为他只有有左儿子才能输出对吧
 //一开始我把俩儿子定义成0，如果这个点他有了下标
 //那就是说一开始就已经遍历过它了
 //那他就是个儿子，要不他啥也不是，那我就不输出他啦！！！ 
     if(tree[now].rson!=0)
         xian(tree[now].rson);
     
 //跟刚才一样 
 
  
 void zhong(int now)
 //跟我刚才解释的先序一样，只不过顺序变成了：
 //左儿子——他爹——右儿子 
 
     if(tree[now].lson!=0)
         zhong(tree[now].lson);
     
     cout<<tree[now].data;
     if(tree[now].rson!=0)
         zhong(tree[now].rson);
     
 
  
 void hou(int now)
 
     if(tree[now].lson!=0)
         hou(tree[now].lson);
     
     if(tree[now].rson!=0)
         hou(tree[now].rson);
     
     cout<<tree[now].data;
 
 //还是跟刚才一样哈哈哈 
 
 int main()
 
     build(0,0);
 //一开始啥也没有，右边那个我定义成啥都行
 //反正他当不了儿子 ,我根本没必要管他 
     xian(1);
     cout<<\'\\n\';
     zhong(1);
     cout<<\'\\n\';
     hou(1);
     cout<<\'\\n\';
     cout<<maxh<<\'\\n\';
     cout<<num<<\'\\n\';
     //完美的输出 
     return 0;
 

（我终于凑够一百行啦！！！）

 

反正我是学不懂了，就先记录到这吧

拜拜！！！

2022/3/24