矩阵微分
Posted faranten
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵微分相关的知识,希望对你有一定的参考价值。
本文地址:https://www.cnblogs.com/faranten/p/16028217.html
转载请注明作者与出处
1 分母布局与分子布局
矩阵微分可以认为是多元微分的一种特殊形式,其中最基础的概念是分母布局(denominator layout)和分子布局(nominator layout)的概念,它决定了矩阵微分的结构。对于\\(\\mathbf x\\in\\mathbb R^M\\)与\\(y=f(\\mathbf x)\\in\\mathbb R\\)而言:
而对于\\(x\\in\\mathbb R\\)与\\(\\mathbf y=f(x)\\in\\mathbb R^N\\)而言:
对于\\(\\mathbf x\\in\\mathbb R^M\\)与\\(\\mathbf y=f(\\mathbf x)\\in\\mathbb R^N\\)而言,其分母布局的一阶导数:
称为雅可比矩阵(Jacobian Matrix)的转置(因为雅可比矩阵采用分子布局)。对于\\(\\mathbf x\\in\\mathbb R^M\\)与\\(y=f(\\mathbf x)\\in\\mathbb R\\)而言,其分母布局的二阶导数:
称为函数\\(f(\\mathbf x)\\)的Hessian矩阵,也写作\\(\\nabla^2f(\\mathbf x)\\),其中第\\(m,n\\)个元素为\\(\\frac\\partial^2y\\partial x_mx_n\\)。
2 导数法则
2.1 加减法则
对于\\(\\mathbf x\\in\\mathbb R^M\\),\\(\\mathbf y=f(\\mathbf x)\\in\\mathbb R^N\\),\\(\\mathbf z=g(\\mathbf x)\\in\\mathbb R^N\\),则
2.2 乘法法则
对于\\(\\mathbf x\\in\\mathbb R^M\\),\\(\\mathbf y=f(\\mathbf x)\\in\\mathbb R^N\\),\\(\\mathbf z=g(\\mathbf x)\\in\\mathbb R^N\\),则
对于\\(\\mathbf x\\in\\mathbb R^M\\),\\(\\mathbf y=f(\\mathbf x)\\in\\mathbb R^S\\),\\(\\mathbf z=g(\\mathbf x)\\in\\mathbb R^T\\)且\\(\\mathbf A\\in\\mathbb R^S\\times T\\),则
对于\\(\\mathbf x\\in\\mathbb R^M\\),\\(y=f(\\mathbf x)\\in\\mathbb R\\),\\(\\mathbf z=g(\\mathbf x)\\in\\mathbb R^N\\),则
2.3 链式法则
在形式上和普通的链式法则一样。
3 完整定义
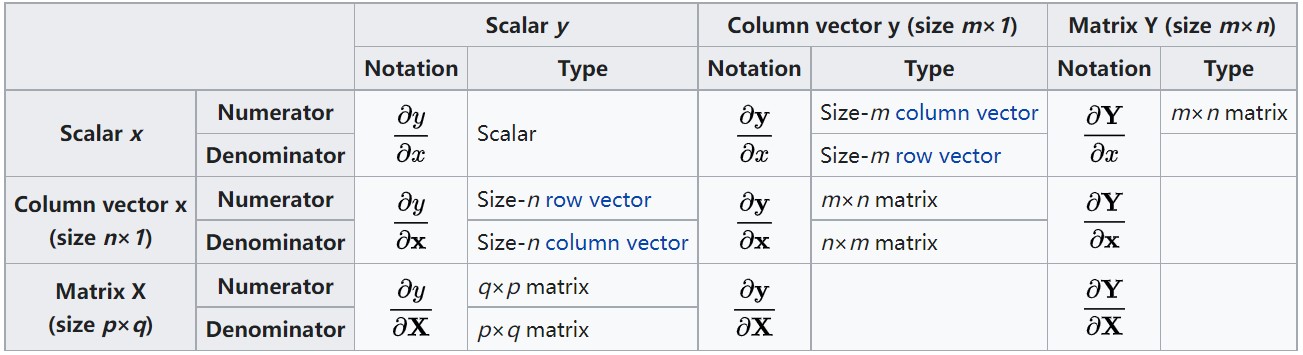
可以看出分母布局和分子布局的区别仅在于转置。
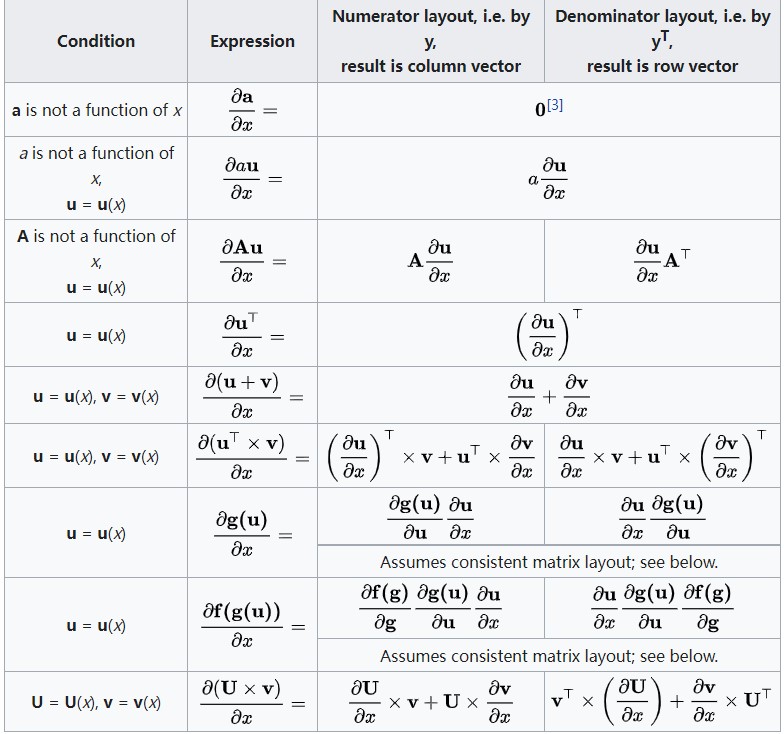
3.1 图1:\\(\\partial\\text向量/\\partial\\text向量\\)
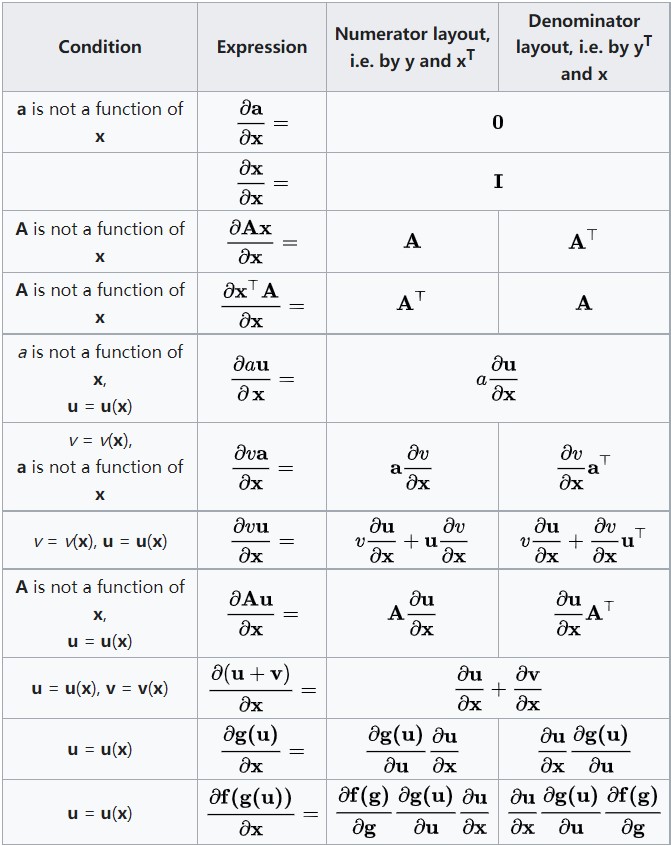
3.2 图2:\\(\\partial\\text标量/\\partial\\text向量\\)
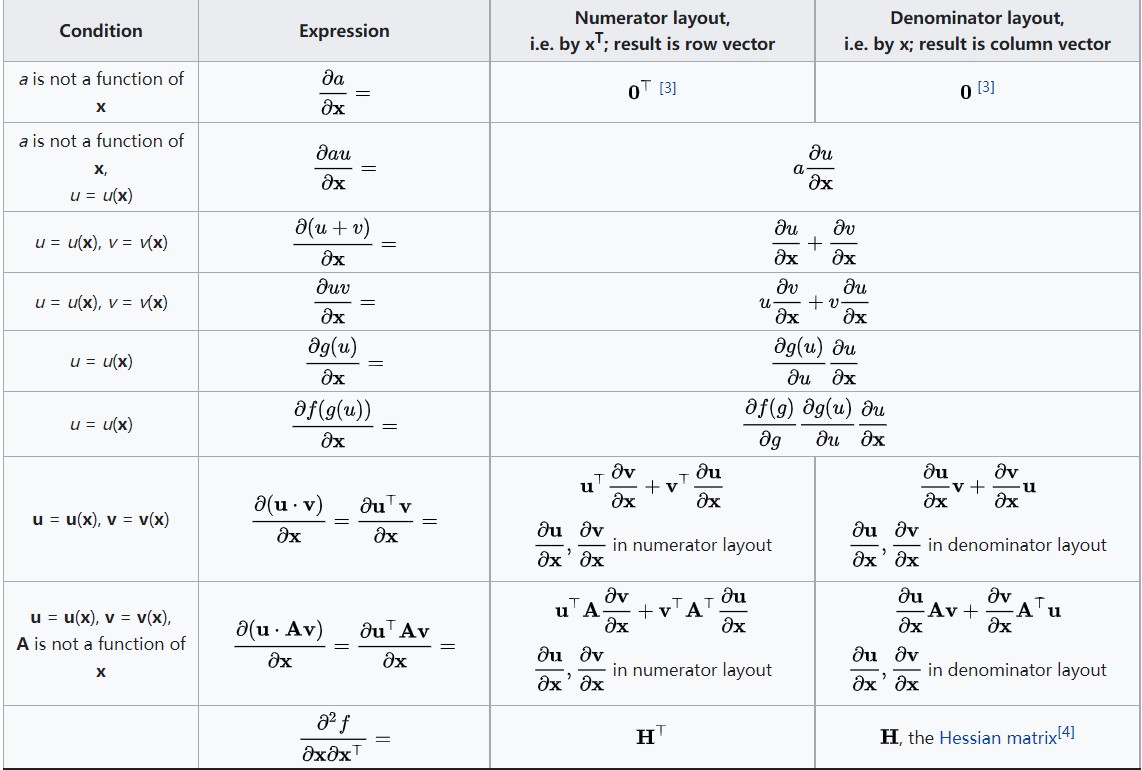
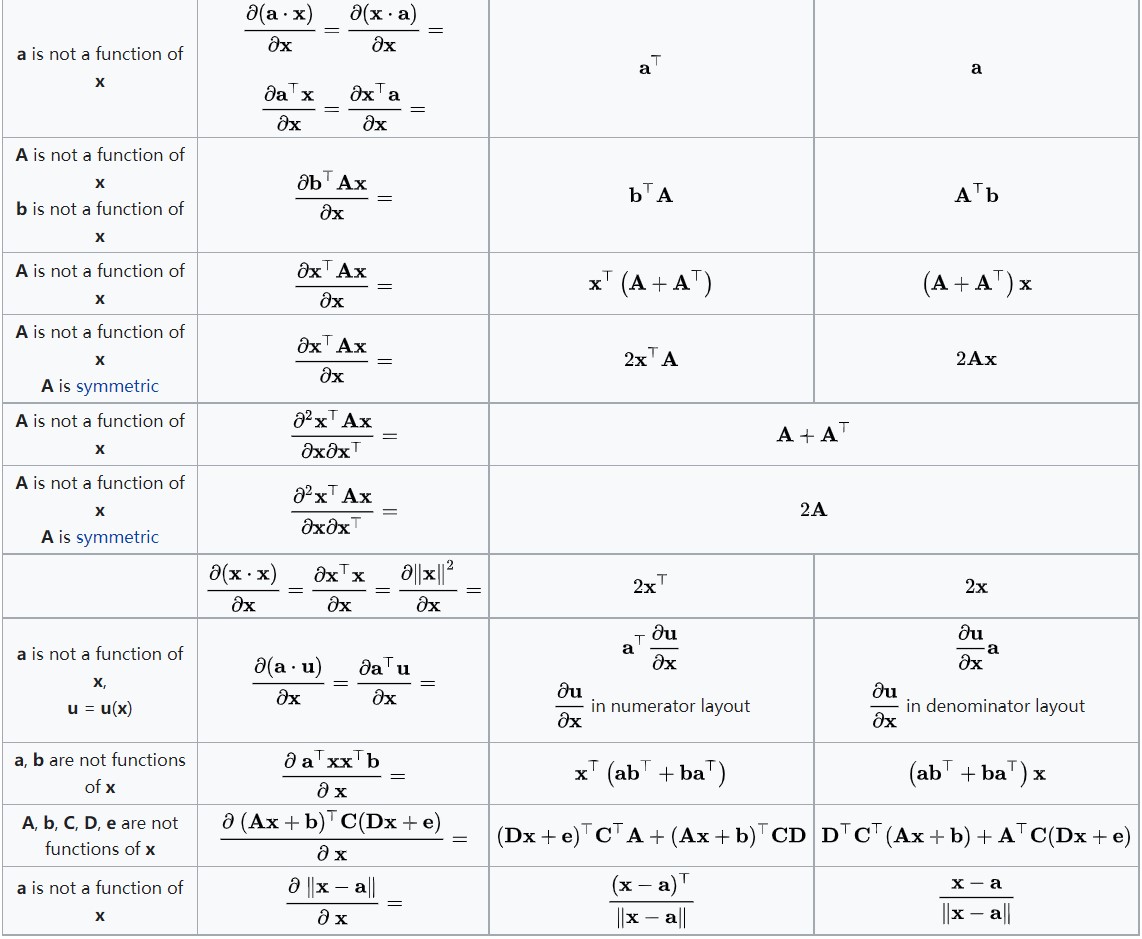
3.3 图3:\\(\\partial\\text向量/\\partial\\text标量\\)
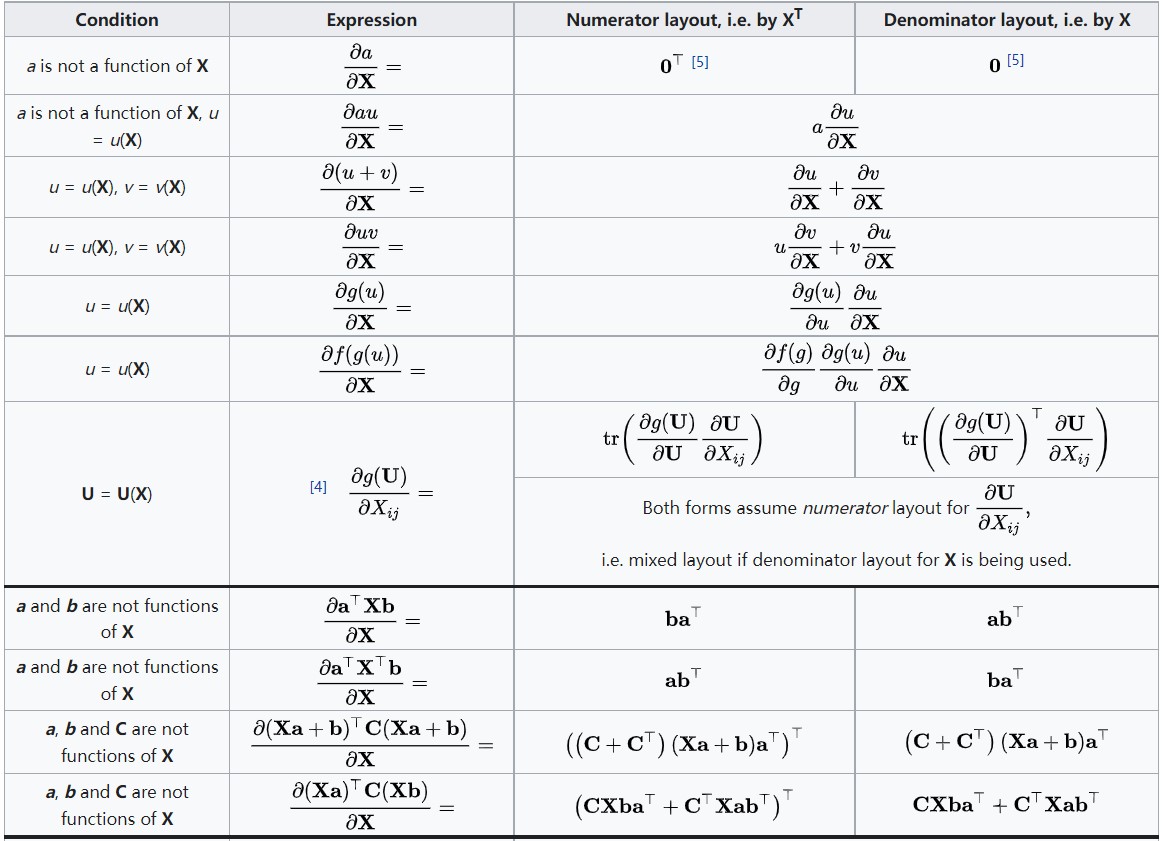
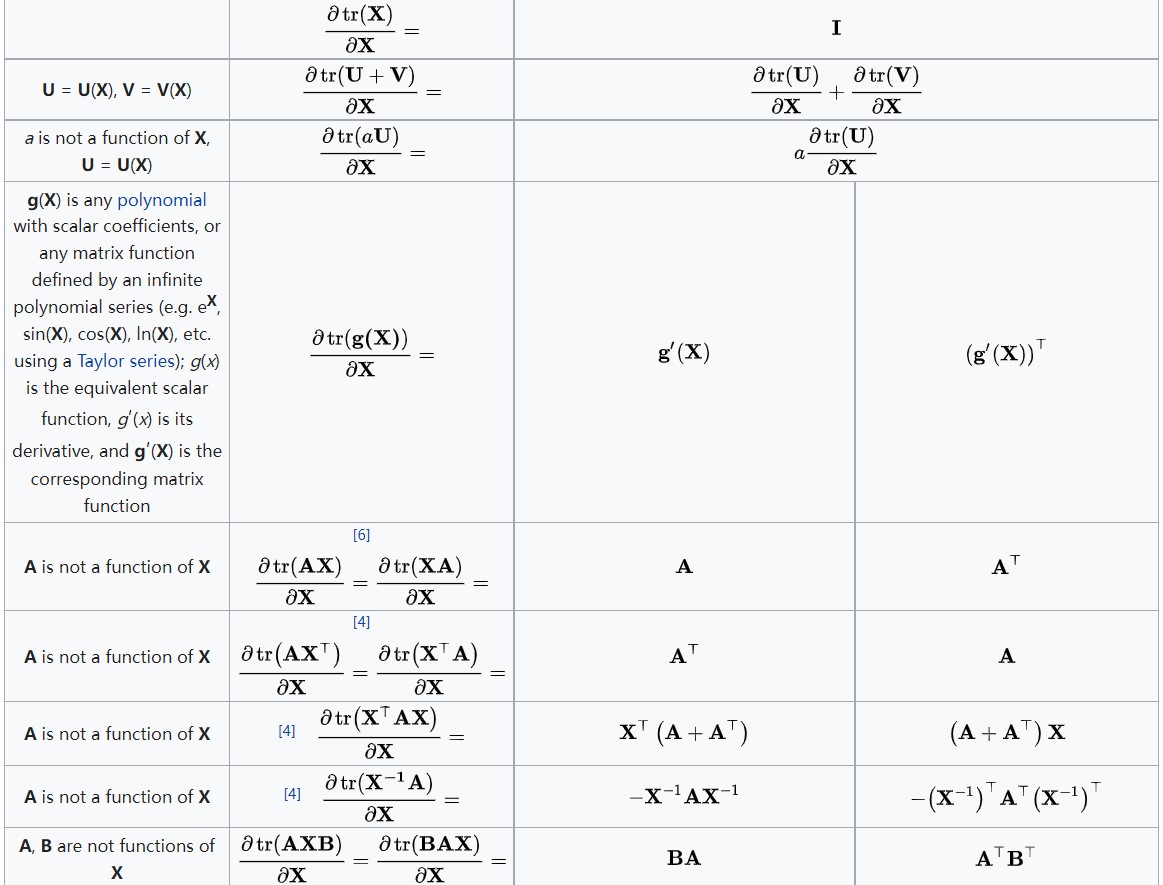
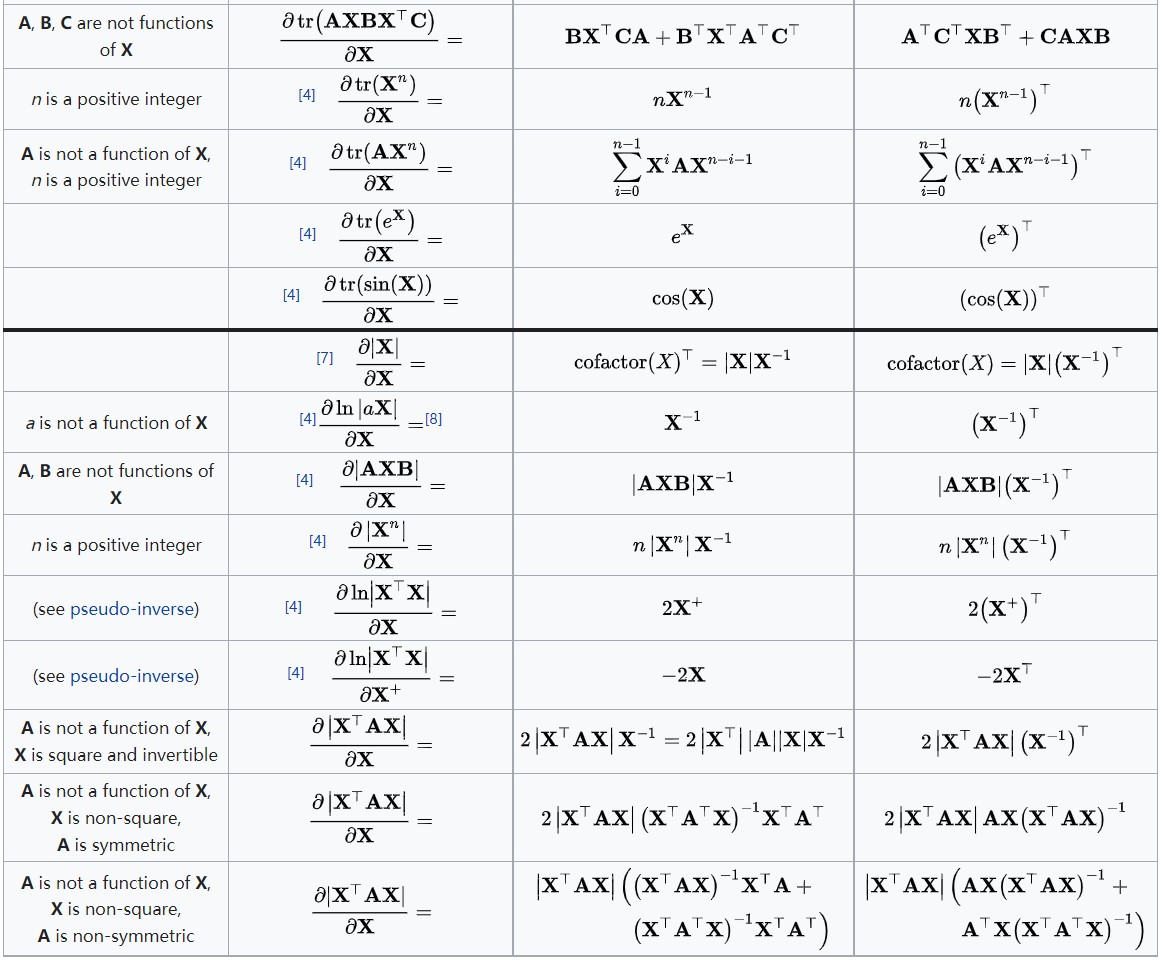
3.4 图4:\\(\\partial\\text标量/\\partial\\text矩阵\\)
3.5 图5:\\(\\partial\\text矩阵/\\partial\\text标量\\)
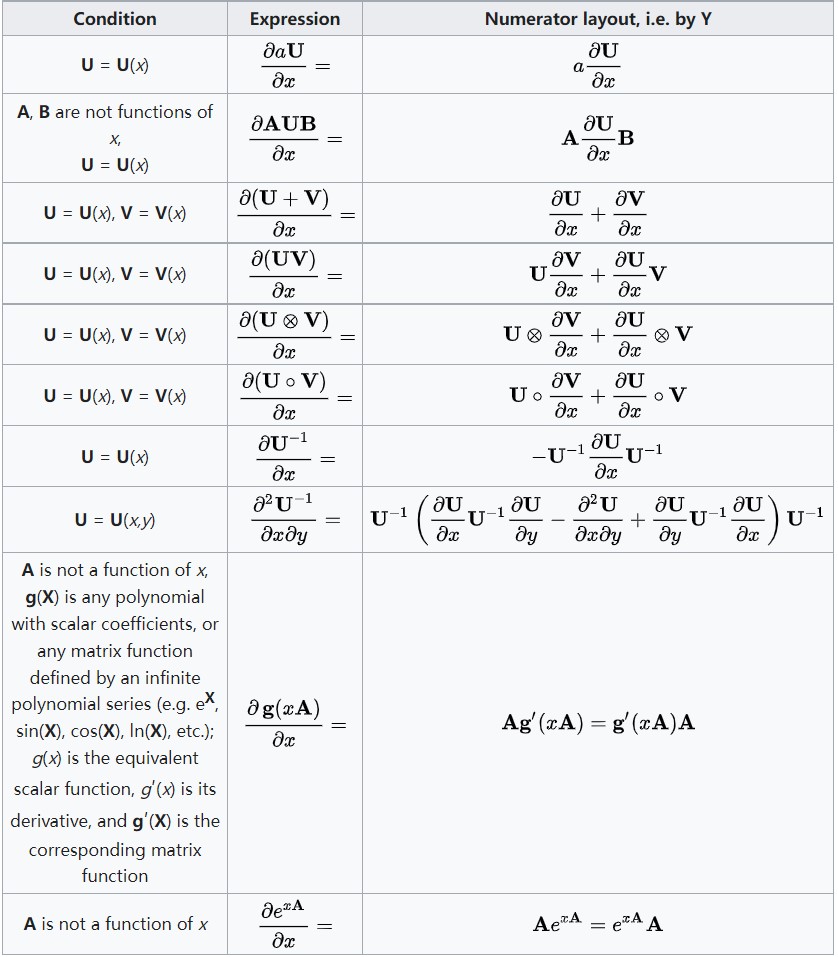
3.6 图6:\\(\\partial\\text标量/\\partial\\text标量\\)链式法则结合矩阵

3.7 图7:\\(\\partial\\text标量/\\partial\\text标量\\)链式法则结合矩阵
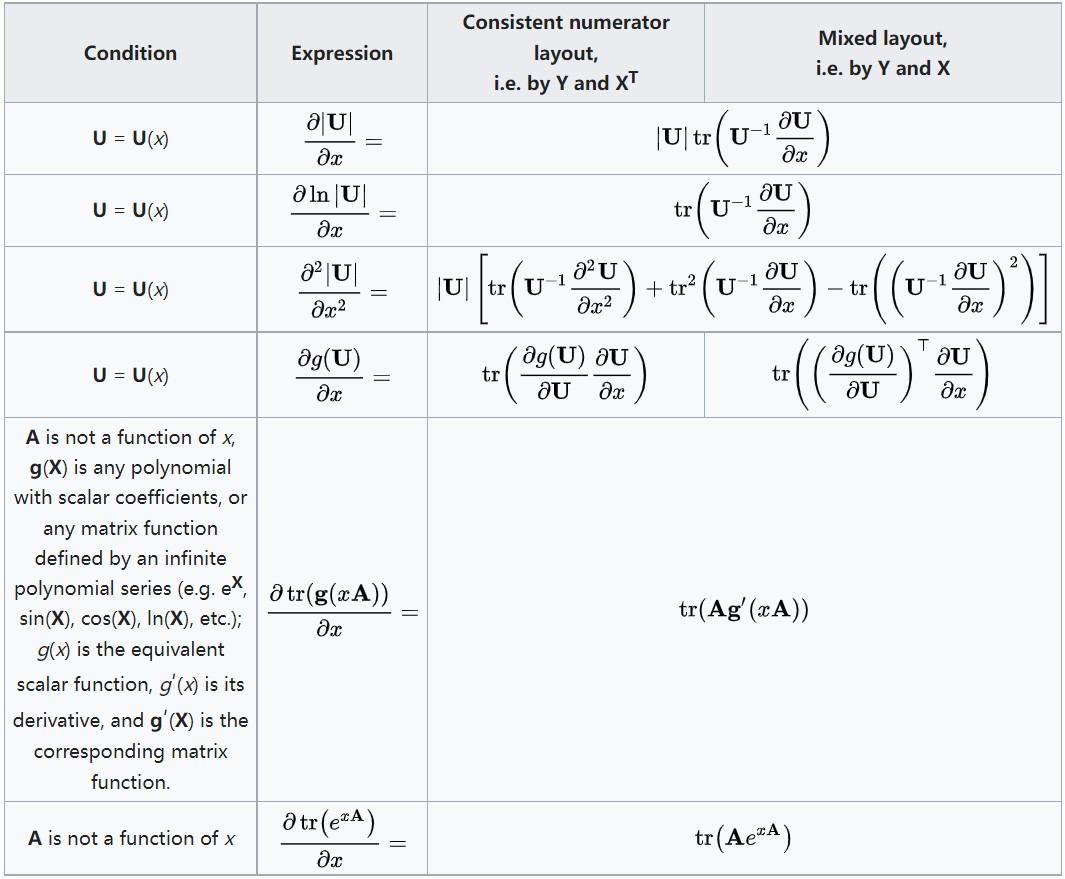
3.8 图8:\\(d(\\text矩阵)\\)

3.9 图9:\\(d(\\text矩阵)\\)

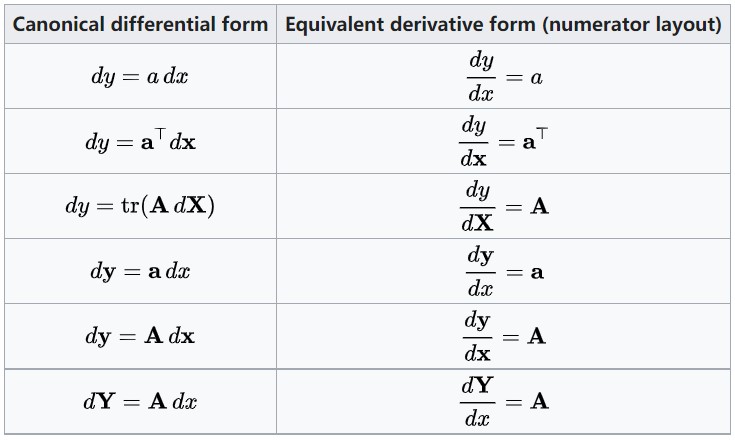
3.10 图10:\\(d/d\\)形式
4 参考资料
- 邱锡鹏,《神经网络与深度学习》,网络发布版本,2021
- Matrix calculus - Wikipedia

以上是关于矩阵微分的主要内容,如果未能解决你的问题,请参考以下文章