[USACO20FEB]Equilateral Triangles P 题解

Posted 2022-03-13 栾竹清影

优雅的暴力。

设三个点为 \\((i,j,k)\\)，则有 \\(6\\) 个未知数即 \\(x_i,x_j,x_k,y_i,y_j,y_k\\)。又因为有 \\(2\\) 条关于这 \\(6\\) 个未知数的方程 \\(ij=jk,ij=ik\\)，所以一定能通过枚举其中的 \\(4\\) 个量来求解，时间复杂度 \\(O(n^4)\\)。

而这个 \\(O(n^4)\\) 的暴力是肉眼可见的跑不满（

---

考虑先枚举点 \\(i\\)，则有以下四种情况：

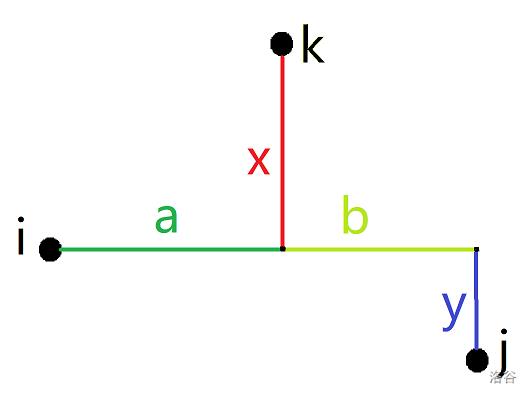
解得 \\(x=a,y=a-b\\)。

其中，\\(a,x>0,0\\le b,y \\le a\\)。

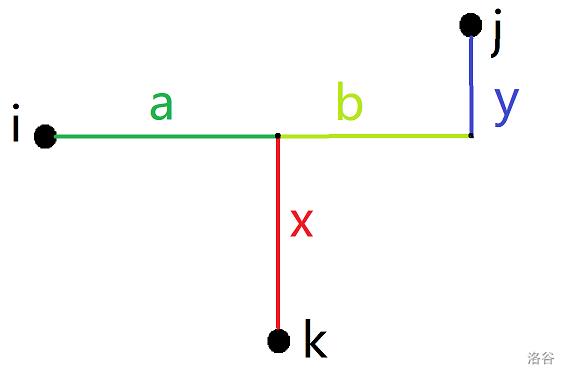
解得 \\(x=a,y=a-b\\)。

其中，其中，\\(a,x>0,0\\le b,y\\le a,\\colorredb\\not= 0\\)。

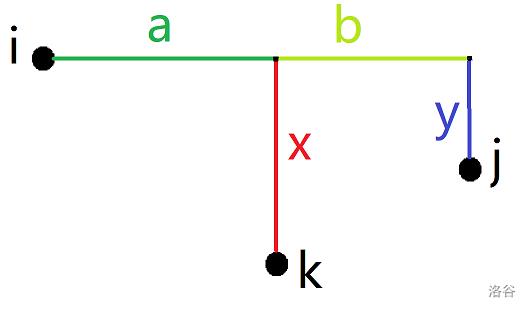
解得 \\(x=2b-a,y=b-a\\)。

其中，\\(0\\le a<b,0\\le x,y\\)。

解得 \\(x=2b-a,y=b-a\\)。

其中，\\(0\\le a<b,0\\le x,y,\\colorreda\\not=0\\)。

---

注意，有些同时存在于两种情况的状态， 需要通过标红的判断去除。

然后就能敲出以下代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=310;
inline int read()
	int x=0;
	char c=getchar();
	for(;(c^\'.\')&&(c^\'*\');c=getchar());
	return c==\'*\';

bool c[maxn][maxn];
int n,ans;
int main()
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			c[i][j]=read();
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!c[i][j]) continue;
			for(int a=0;a<=n;a++)
				for(int b=0;b<=a;b++)
					if(a&&i+a<=n&&j+a<=n&&i-a+b>0&&j+a+b<=n)
						ans+=(c[i+a][j+a]&c[i-a+b][j+a+b]);
					if(a&&b&&i-a>0&&j+a<=n&&i+a-b<=n&&j+a+b<=n)
						ans+=(c[i-a][j+a]&c[i+a-b][j+a+b]);
				
				for(int b=a+1;b<=n;b++)
					if(i-b-b+a>0&&j+a<=n&&i-b+a>0&&j+a+b<=n)
						ans+=(c[i-b-b+a][j+a]&c[i-b+a][j+a+b]);
					if(a&&i+b+b-a<=n&&j+a<=n&&i+b-a<=n&&j+a+b<=n)
						ans+=(c[i+b+b-a][j+a]&c[i+b-a][j+a+b]);
				
			
		
	printf("%d\\n",ans);
	return 0;
 

然后你会获得 \\(51pt\\) 的高分。

容易发现，代码中搜索到了许多冗余的状态，考虑将判断放到循环之外：

#include<bits/stdc++.h>
using namespace std;
const int maxn=310;
inline int read()
	int x=0;
	char c=getchar();
	for(;(c^\'.\')&&(c^\'*\');c=getchar());
	return c==\'*\';

bool c[maxn][maxn];
int n,ans;
int main()
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			c[i][j]=read();
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!c[i][j]) continue;
			for(int a=0;a<=n;a++)
				if(a&&i+a<=n&&j+a<=n)
					for(int b=max(a-i+1,0);b<=a&&j+a+b<=n;b++)
						ans+=(c[i+a][j+a]&c[i-a+b][j+a+b]);
				if(a&&i-a>0&&j+a<=n)
					for(int b=max(i+a-n,1);b<=a&&b<=n-j-a;b++)
						ans+=(c[i-a][j+a]&c[i+a-b][j+a+b]);
				if(j+a<=n)
					for(int b=a+1;j+a+b<=n&&b+b<i+a;b++)
						ans+=(c[i-b-b+a][j+a]&c[i-b+a][j+a+b]);
				if(a&&j+a<=n)
					for(int b=a+1;j+a+b<=n&&b+b<=n-i+a;b++)
						ans+=(c[i+b+b-a][j+a]&c[i+b-a][j+a+b]);
			
		
	printf("%d\\n",ans);
	return 0;
 

然后就过了。

祝AC。