UVA 1487 Volume

Posted 2022-02-27 曾梵瑀

本文作者为初中生，可能表述不规范。

求两个中心重合，轴垂直的全等圆柱体的体积并，半径为 \\(r\\)，高为 \\(h\\)。

其等于两个圆柱体积减去体积交。

我们知道 \\(V=\\displaystyle\\int^h_0S(x)dx\\)。

于是考虑用这个来搞体积交。

用横截面来截这个神奇的东西：从蓝线（\\(0\\)）截到红线（\\(r\\)）。

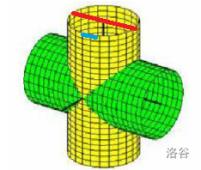
截出来

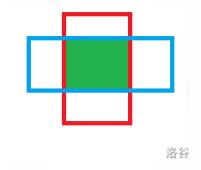
求绿色部分体积。令其为 \\(S(x)\\)，其中 \\(x\\) 为目前的截面到蓝色那个点的距离。

则 \\(Ans=2r^2h\\pi-2\\times\\displaystyle\\int^r_0S(x)dx\\)。

即求红线长度。

相交弦定理得 \\(len=2\\sqrt2xr-x^2\\)。

注意当 \\(h\\) 更小时这个为 \\(h\\)，可以画图理解。

然后就直接积分了。

\\(\\forall x\\in [0,r],(2\\sqrt2xr-x^2)\'>0\\)，故这玩意单调递增。

然后可以二分求出其等于 \\(h\\) 时的 \\(x\\) 值，设为 \\(x_0\\)。

注意，正如题目提醒的那样，\\(2r<h\\) 时，方程无解，认为 \\(x_0=r\\)。

\\(\\displaystyle\\int^r_0S(x)dx=\\int^x_0_0\\int \\pi(2\\sqrt2xr-x^2)^2 dx+\\int^h_x_0\\int h^2 dx\\)

\\(\\displaystyle\\int \\pi(2\\sqrt2xr-x^2)^2=\\int8\\pi rx-4\\pi x^2=4\\pi r x^2-\\frac43\\pi x^3\\)

\\(\\displaystyle\\int h^2=h^2x\\)

\\(\\displaystyle\\int^r_0S(x)dx=4\\pi rx_0^2-\\frac43\\pi x^3+h^3-h^3x_0\\)

\\(Ans=\\displaystyle 2\\pi r^2h-2(4\\pi rx_0^2-\\frac43\\pi x^3+h^3-h^3x_0)\\)

YJX AK IOI